2、第二个特性----以集合为单位进行操作
在我们以往面向过程语言不同,SQL是一门面向集合的一门语言。由于习惯了面向过程的思考方式,导致我们在使用SQL时往往也陷入之前的思维定式。
我们现在分别创建customers表和orders表


customers orders
我们最直观看到数据库的数据组织方式是通过 视图查询出来,就像上面两张图我们所看到的一样。
而数据库存储数据其实是如下两张图
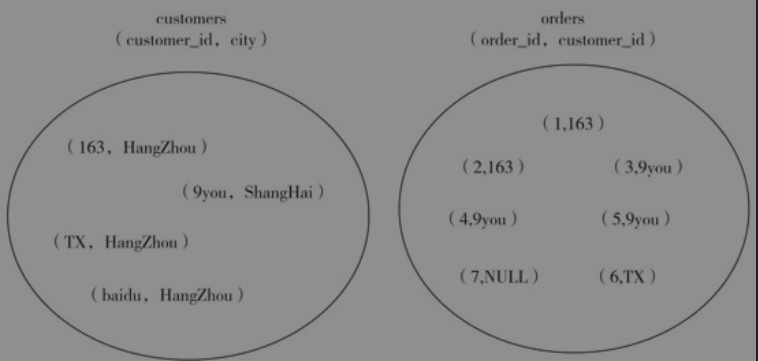
customers和orders的集合
想了下怎么讲解这个以集合为单位进行操作最后还得通过案例进行说明,而最能体现这个特性就在于对 Having 的使用。
例一:求众数
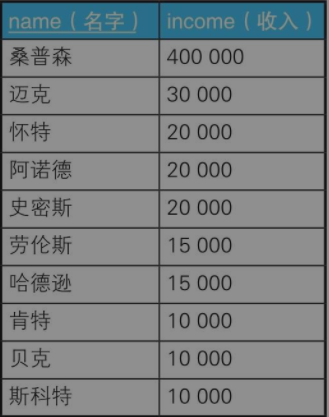
以面向过程的思路分析这道题是如下步骤:
1)创建一个MAP<item,num>集合,item是数字,num是出现的次数。
2)对输入的数组集合作遍历,并判断MAP中是否存在该数字,若存在则将num+1,若不存在则将数字放入MAP中。
3)对MAP中num属性提取出最大值。
4)通过最大num值在MAP中找到相应的数字。
而在面向集合中解题思路应该是这样的:
1)对数组列表中每一个数字进行分组
2)计算每一组数字的个数 并 要大于任何一组数字的个数 ,该数字即为该数组的众数。
--求众数SQL语句(1):使用谓词 SELECT income,COUNT(*) AS cnt FROM Graduates GROUP BY income HAVING COUNT(*) >= ALL (SELECT COUNT(*) FROM Graduates GROUP BY income) --求众数SQL语句(2):使用极值函数 SELECT income,COUNT(*) AS cnt FROM Graduates GROUP BY income Having COUNT(*) >= ( SELECT MAX(cnt) FROM (SELECT COUNT(*) AS cnt FROM Graduates GROUP BY income) TMP);
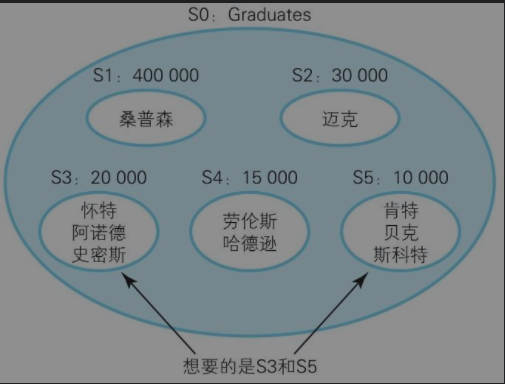
分组集合操作
例二:求中位数
面向过程解析:
1)对集合进行大小排序。
2)如果是奇数则取集合中间一个数字为中位数,如果是偶数则取中间两个数字的平均值为中位数。
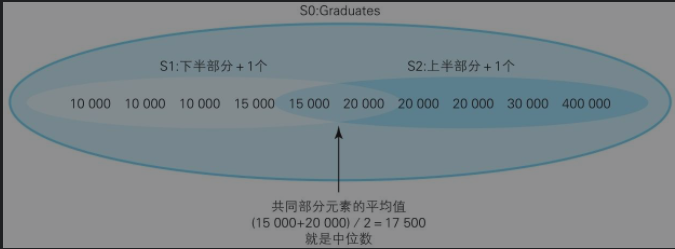
面向集合解析:
1)将集合按大小分为上半部分和下半部分两个子集
2)让两个子集同时拥有的元素取平均值就为中位数
SELECT AVG(DISTINCT income) FROM (SELECT a.income FROM Graduates a,Graduates b GROUP BY a.income HAVING SUM(CASE WHEN a.income >= b.income THEN 1 ELSE 0 END) >= COUNT(*)/2 AND SUM(CASE WHEN a.income <= b.income THEN 1 ELSE 0 END) >= COUNT(*)/2 )TMP
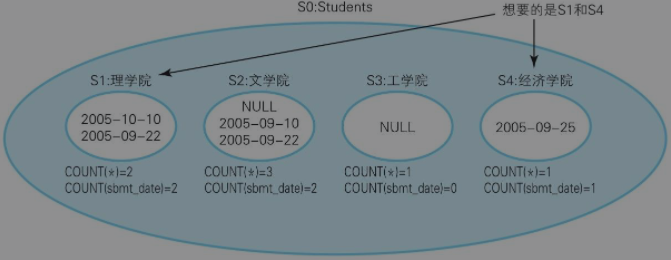
例三:查询所有学生都提交了报告的学院
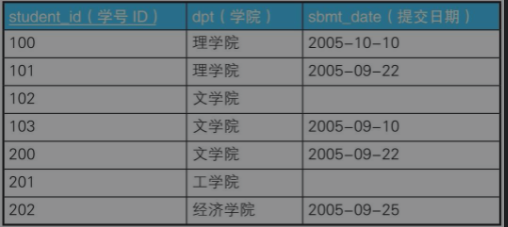
面向过程解析:
1)对数组集合进行循环遍历筛选出提交日期为空的学院
2)对第一步产生的结果再原数组集合作差集,筛选出所有提交报告的学院
面向集合解析:
1)对集合按照学院分组,并统计每个学院已提交报告的数量
2)对第一步产生结果与原集合按学院分组后的数量进行比对,若数量一致则为已提交所有报告的学院
SELECT COUNT(*) FROM Students GROUP BY COUNT(*) = COUNT(sbmt_date)
例四:关系除法运算

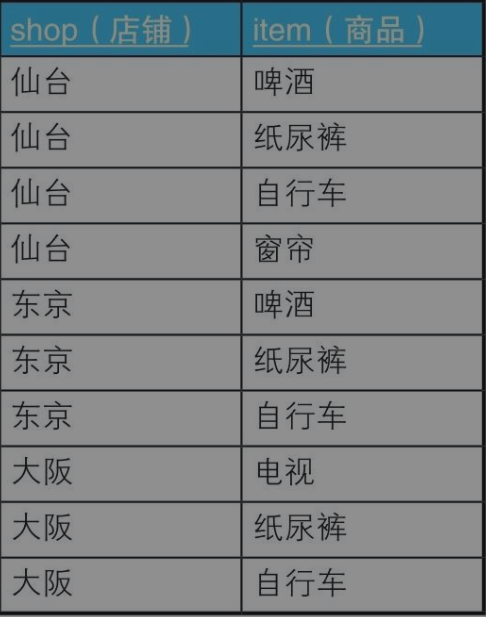
Items ShopItems
1.查询包含在Items所有商品的商店
面向过程解析:
1)在 shopitems 表中按照店铺作数组拆分
2)对拆分出来的数组中所售商品按照Items进行遍历比对,若检测其中任意一个Items商品不在该数组中则将其筛选出。
面向集合解析:
1) 将shopitems按照店铺分组 并 对 shopitems 与 items 按照 item 做关联
2) 统计关联后的分组结果数量是否和Items表中商品数量是否一致
/*查询店铺中包含表Items中所有商品的店铺*/ SELECT shop FROM ShopItems a,Items b WHERE a.item = b.item GROUP BY shop HAVING COUNT(*) = (SELECT COUNT(*) FROM Items)
2.精确关系除法
第一个问题按照上述逻辑会筛选出东京和仙台,而仙台还包含有“窗帘”这一项在Items是不存在的,这样的查询称之为 带余除法
现在我们要从shopitems筛选出与items完全重合店铺信息,就是只需要筛选出东京。这个问题称之为 精确关系除法。
1) 将shopitems按照店铺分组 并 对 shopitems 与 items 按照 item 做外关联,确保shopitems中的元素不会缺失
2)让匹配到的 items 中的元素与 Items数量作比较是否一致
3)比较店铺中所有商品与匹配到的商品数量是否一致
通过(2)能够确保 在Items中存在的商品都存在于店铺中
通过(3)能够确保 店铺中的商品数量是与匹配到的商品数量是一致的
在有了(2)的前提下,若满足(3)的条件,则说明店铺中商品是和商品表里的商品是一一对应的。
/*精确关系除法*/ SELECT shop FROM ShopItems a LEFT JOIN Items b ON a.item = b.item GROUP BY shop HAVING COUNT(b.item) = (SELECT COUNT(*) FROM Items) AND COUNT(a.item) = COUNT(b.item)
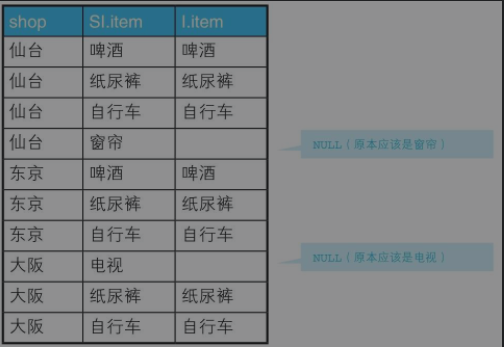
3.这里我们再解析下什么是关系除法
首先这里我们给出它的数学定义:

然后我们再按照上述定义来解析这两道题
1)shopitems表中存在两个属性,shop属性和Item属性;items表中存在item一个属性;他们的共同属性为item
2)Items在shopitems上的投影为

2)shopitems表分量shop属性的象集为:
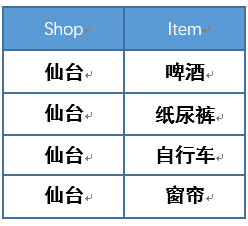

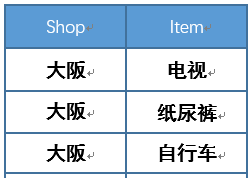
象集1 象集2 象集3
3)那么我们能看3个象集中包含关系Items在shopitems上的投影的是 象集1和象集2
最后我们再通过下面两张图就更清楚,带余除法和精确除法的关系了

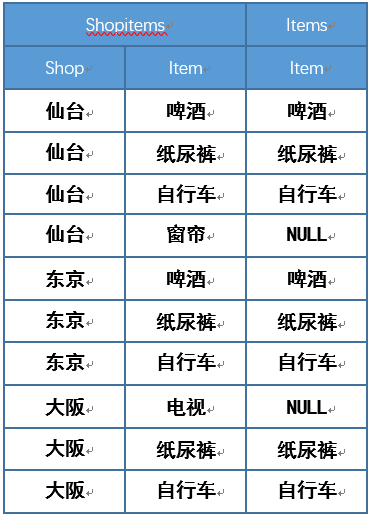
带余除法 精确除法
这就是关系除法的原理,那为什么这样的运算称之为除法运算呢?
答:因为这样会产生一个结果(商),通过再与我们的除数进行笛卡尔积运算能够得到被除数的子集或者被除数本身。由于笛卡尔积运算我们称之为乘法运算,那么作为它的逆向运算就为除法运算了。
例五:行转列 制作交叉表
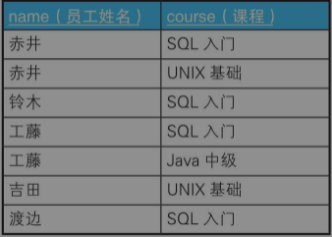

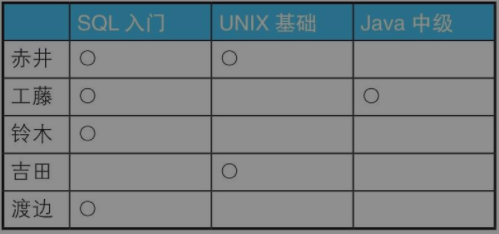
那么本题还是应该使用集合的思想来解题,我们将原数据按下图整理
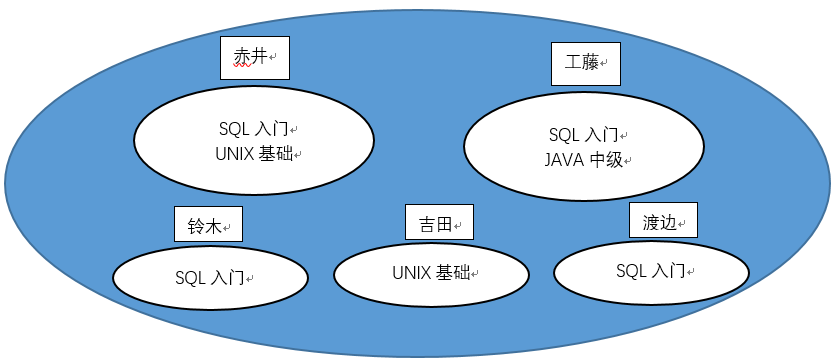
我们按人名对集合进行分为5组后,Group by name 的 name的值 就能作为我们的侧边栏,而表头则需要我们自己作定义,根据每个分组里面的值进行判断。
举例:赤井这个分组我们根据已知表头中三个课程进行判断,如果相同则标记为‘O’;不同则标记为‘X’。
/*课程记录一览表*/ SELECT a.name, MAX(CASE WHEN course = 'SQL入门' THEN '○' ELSE '×' END) AS 'SQL入门', MAX(CASE WHEN course = 'UNIX基础' THEN '○' ELSE '×' END) AS 'UNIX基础', MAX(CASE WHEN course = 'Java中级' THEN '○' ELSE '×' END) AS 'Java中级' FROM Courses a GROUP BY a.name
例六:移动累计值

Accounts
1)求截止到某个处理日期的处理金额的累计值,实际上就是求截止到那个时间点的账户余额
本题还是得用集合的思想解决,但是现在日期都不同,那么现在以什么作为分组呢?
答案是我们需要作一次自关联,让其产生一个每个日期小于等于它本身的日期集合,然后对这个集合统一作累计计算。
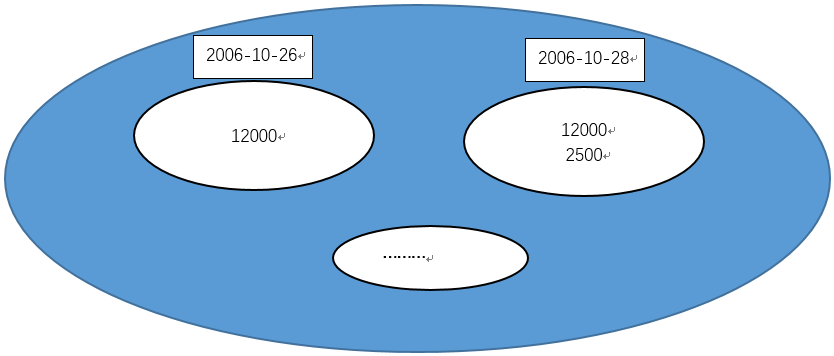
/* 求累计值 */ SELECT prc_date, prc_amt, (SELECT SUM(prc_amt) FROM Accounts b WHERE a.`prc_date` >= b.prc_date) AS onhand_amt FROM Accounts a
2)我们考虑一下如何以3次处理为单位求累计值,即移动累计值。所谓移动,指的是将累计的数据行数固定(本例中为3行),一行一行地偏移,如下表所示。

还是根据刚才所讲按每个日期和每个比他本身小的日期作分组,不过这次还要加上在区间范围不超过3的条件
/*求移动累计值*/ SELECT a.`prc_date`,SUM(b.`prc_amt`) FROM Accounts a,Accounts b WHERE a.`prc_date` >= b.`prc_date` AND (SELECT COUNT(*) FROM Accounts c WHERE c.`prc_date` BETWEEN b.`prc_date` AND a.`prc_date`)<=3 GROUP BY a.`prc_date`
对于区间不满三行的数据则不输出
/*不满三行不作输出*/ SELECT a.`prc_date`,SUM(b.`prc_amt`) FROM Accounts a,Accounts b WHERE a.`prc_date` >= b.`prc_date` AND (SELECT COUNT(*) FROM Accounts c WHERE c.`prc_date` BETWEEN b.`prc_date` AND a.`prc_date`)<=3 GROUP BY a.`prc_date` HAVING COUNT(*) = 3
例七:查询重叠的时间区间
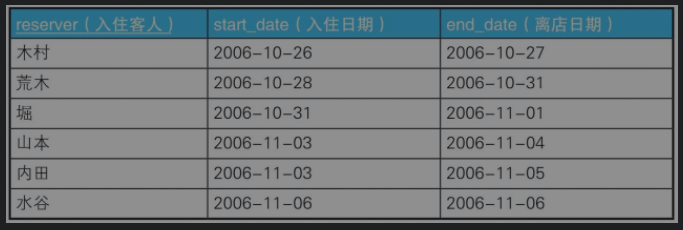
Reservations
本题作自关联,为每一个时间段预先制造一个分组集合,在集合内先完成条件筛选。
/**查询住宿重叠时间**/ SELECT reserver, astart, aend FROM ( SELECT a.reserver,a.start_date AS astart,a.end_date AS aend,b.start_date AS bstart,b.end_date AS bend FROM Reservations a,Reservations b WHERE a.reserver <> b.reserver )tmp WHERE bstart BETWEEN astart AND aend OR bend BETWEEN astart AND aend OR bstart BETWEEN astart AND aend AND bend BETWEEN astart AND aend
例8:查询两个集合是否相等
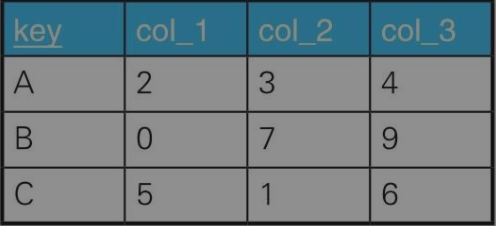
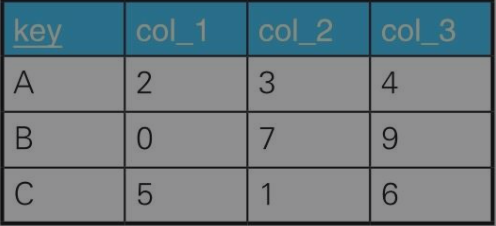
tbl_A tbl_B
如何比较这两个集合元素是否是相等的呢
1)那我们可以使用 A+B=A=B 的条件来判断这样的场景
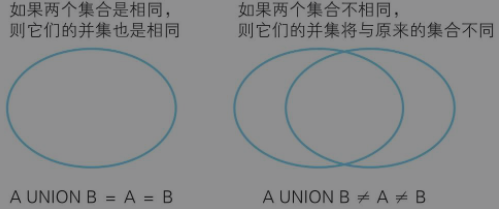
/*判断集合是否相等*/ SELECT COUNT(*) FROM ( SELECT * FROM tlb_A UNION SELECT * FROM tlb_B )TMP
2)第一种解法就要先确定A和B的行数,那现在想一想能不能直接对A、B进行比较呢?
那可以利用两个集合的并集和差集来判定其相等性。如果用SQL语言描述,那就是“如果A UNION B = A INTERSECT B,则集合A和集合B相等”。
(A ∪ B ) = (A ∩ B) ⇔ (A = B)
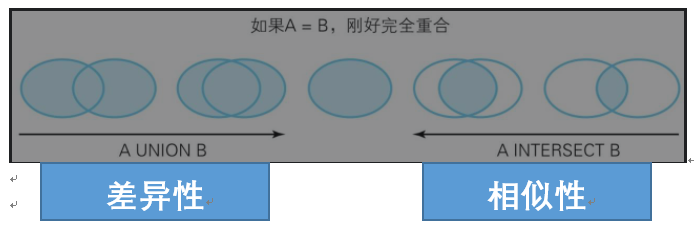
/*判断集合是否相等*/ SELECT CASE WHEN COUNT(*) = 0 THEN '相等' ELSE '不相等' END AS result FROM ((SELECT * FROM tbl_A UNION SELECT * FROM tbl_B) EXCEPT (SELECT * FROM tbl_A INTERSECT SELECT * FROM tbl_B) ))TMP;
例9:寻找相等子集
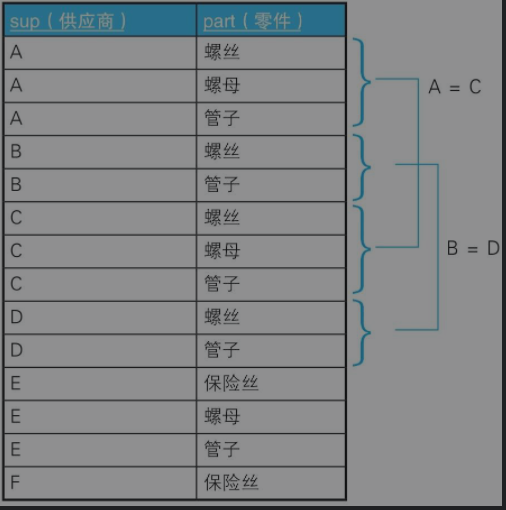
SupParts
问题:找出经营的零件在种类数和种类上都完全相同的供应商组合。
SQL并没有提供任何用于检查集合的包含关系或者相等性的谓词。IN 谓词只能用来检查元素是否属于某个集合,而不能检查集合是否是某个集合的子集。
那我们就先给出答案
/*寻找相等子集*/ SELECT a.`sup`,b.`sup` FROM SupParts a,SupParts b WHERE a.`part` = b.`part` AND a.`sup` < b.`sup` GROUP BY a.`sup`,b.`sup` HAVING COUNT(*) = (SELECT COUNT(*) FROM SupParts c WHERE a.`sup` = c.`sup`) AND COUNT(*) = (SELECT COUNT(*) FROM SupParts d WHERE b.`sup` = d.`sup`)
大家对此是不是比较熟悉
其实这个思路和例四很像,只不过例四是只检查一个集合是否要和另一个集合相等。而本题是需要同时检查两个集合是否都和第三个集合相等。这样保证集合A和集合B关联后记录不会丢失,因为C和D是完整的记录而且都是自己本身。