本文参考
出自LeetCode上的题库 —— 环形链表II,哈希表和快慢指针两种解法都需要O(n)的时间,但快慢指针仅占用O(1)的空间
https://leetcode-cn.com/problems/linked-list-cycle-ii/
环形链表问题
给定一个链表的头节点 head,返回链表开始入环的第一个节点(不允许修改链表)
如果链表无环,则返回null。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环
示例1:
输入:head = [3,2,0,-4]
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点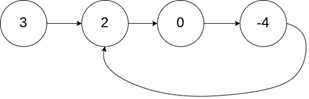
示例2:
输入:head = [1,2]
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点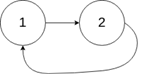
示例3:
输入:head = [1]
输出:返回 null
解释:链表中没有环
解题思路
首先是特殊情况,当没有节点,或有节点却不存在环的情况下,容易通过节点或节点的next指针是否空进行判断
当节点间存在环路时,第一种直观的解法,使用一个指针沿着链路走下去,每走一步将节点存入set集合,当碰到重复出现的节点时,该节点就是环路的入口;
第二种解法需要应用两遍双指针,可能刚接触这道题时已经想到了快慢指针,但是我们无法保证快指针和慢指针相遇的位置一定是环路的入口,以至于否定了这种解法。此处需要一定的数学分析,在快慢指针相遇的位置引入第三个指针:
令总节点数为$n$,头节点为$head$,环路的入口节点为$entry$,环路中快慢指针相遇的节点位置为$meet$,定义距离$a=Distance(head,entry)$,距离$b=Distance(entry,meet)$,距离$c=Distance(meet,entry)$,满足$n=a+b+c$
当快慢指针相遇时,快指针走过的路径长度为$d_{fast}=a+n(b+c)+b$,慢指针走过的路径长度为$d_{slow}=a+b$,我们预先设置快指针每次走两步,慢指针每次走一步,则$d_{fast}=2d_{slow}=a+n(b+c)=2(a+b)$,化简得$a=c+(n-1)(b+c)$,$a$的长度是$c$的长度加上$(n-1)$圈的环路长度
因此,我们引入第三个指针ptr,慢指针从相遇位置开始移动,ptr从头指针开始移动,由公式$a=c+(n-1)(b+c)$可知,二者相遇的位置即为环路的路口
哈希表解法
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def detect_cycle_1(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return None
node_set = set()
curr_node = head
while curr_node not in node_set:
node_set.add(curr_node)
if curr_node.next is None:
return None
else:
curr_node = curr_node.next
return curr_node
快慢指针解法
def detect_cycle_2(self, head: ListNode) -> ListNode:
slow = fast = head
while fast is not None:
# 慢指针每次走一步
slow = slow.next
if fast.next is None:
return None
# 快指针每次走两步
fast = fast.next.next
# 快慢指针相遇
if fast == slow:
ptr = head
# 建立新的双指针走法
while ptr != slow:
ptr = ptr.next
slow = slow.next
return ptr
return None