Looploop
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 781 Accepted Submission(s): 220
Problem Description
XXX gets a new toy named Looploop. The toy has N elements arranged in a loop, an arrow pointing to one of the elements, and two preset parameters k1 and k2. Every element has a number on it.
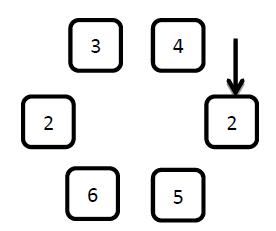
The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy.
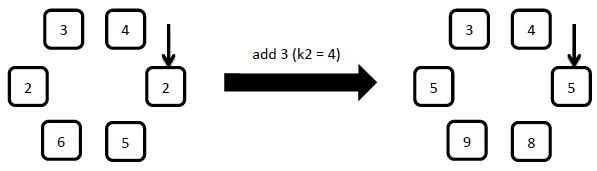
1: add x
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.
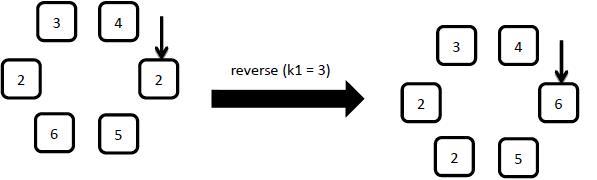
2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.
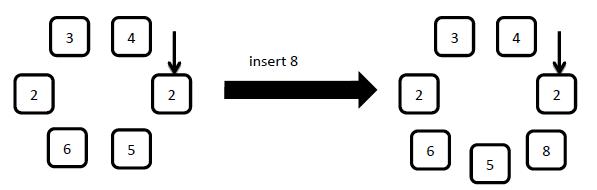
3: insert x
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.
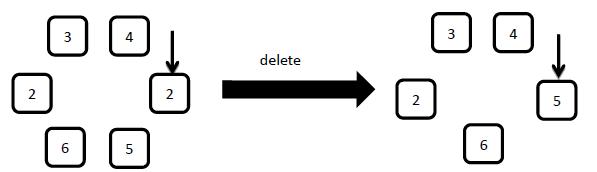
4: delete
Delete the element the arrow pointed and then move the arrow to the right element.
5: move x
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.
6: query
Output the number on the arrow pointed element in one line.
XXX wants to give answers to every query in a serial of operations.

The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy.
1: add x
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.

2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.

3: insert x
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.

4: delete
Delete the element the arrow pointed and then move the arrow to the right element.

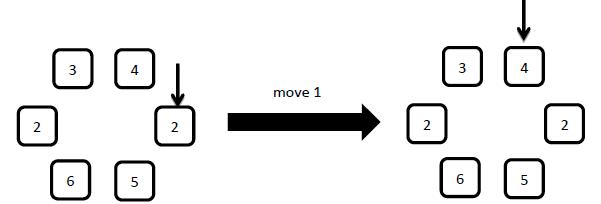
5: move x
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.

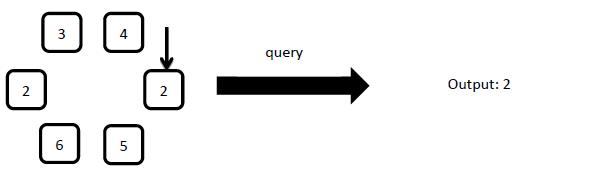
6: query
Output the number on the arrow pointed element in one line.

XXX wants to give answers to every query in a serial of operations.
Input
There are multiple test cases.
For each test case the first line contains N,M,k1,k2(2≤k1<k2≤N≤105, M≤105) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy.
Second line contains N integers ai(-104≤ai≤104) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning.
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations.
The input ends with a line of 0 0 0 0.
For each test case the first line contains N,M,k1,k2(2≤k1<k2≤N≤105, M≤105) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy.
Second line contains N integers ai(-104≤ai≤104) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning.
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations.
The input ends with a line of 0 0 0 0.
Output
For each test case, output case number in the first line(formatted as the sample output). Then for each query in the case, output the number on the arrow pointed element in a single line.
Sample Input
5 1 2 4
3 4 5 6 7
query
5 13 2 4
1 2 3 4 5
move 2
query
insert 8
reverse
query
add 2
query
move 1
query
move 1
query
delete
query
0 0 0 0
Sample Output
Case #1:
3
Case #2:
2
8
10
1
5
1
Source
用splay tree解决很容易实现。
1 /* *********************************************** 2 Author :kuangbin 3 Created Time :2013-10-22 16:10:40 4 ************************************************ */ 5 6 #include <stdio.h> 7 #include <string.h> 8 #include <iostream> 9 #include <algorithm> 10 #include <vector> 11 #include <queue> 12 #include <set> 13 #include <map> 14 #include <string> 15 #include <math.h> 16 #include <stdlib.h> 17 #include <time.h> 18 using namespace std; 19 20 #define Key_value ch[ch[root][1]][0] 21 const int MAXN = 200010; 22 23 int pre[MAXN],ch[MAXN][2],key[MAXN],size[MAXN]; 24 int root,tot1; 25 int s[MAXN],tot2; 26 int rev[MAXN],add[MAXN]; 27 int n,q,k1,k2; 28 int a[MAXN]; 29 int tp;//指针 30 void NewNode(int &r,int father,int k) 31 { 32 if(tot2)r = s[tot2--]; 33 else r = ++tot1; 34 pre[r] = father; 35 ch[r][0] = ch[r][1] = 0; 36 key[r] = k; 37 add[r] = 0; 38 rev[r] = 0; 39 size[r] = 1; 40 } 41 void Update_Rev(int r) 42 { 43 if(!r)return; 44 swap(ch[r][0],ch[r][1]); 45 rev[r] ^= 1; 46 } 47 void Update_ADD(int r,int ADD) 48 { 49 if(!r)return; 50 key[r] += ADD; 51 add[r] += ADD; 52 } 53 54 void push_up(int r) 55 { 56 size[r] = size[ch[r][0]] + size[ch[r][1]] + 1; 57 } 58 void push_down(int r) 59 { 60 if(add[r]) 61 { 62 Update_ADD(ch[r][0],add[r]); 63 Update_ADD(ch[r][1],add[r]); 64 add[r] = 0; 65 } 66 if(rev[r]) 67 { 68 Update_Rev(ch[r][0]); 69 Update_Rev(ch[r][1]); 70 rev[r] = 0; 71 } 72 } 73 void Build(int &x,int l,int r,int father) 74 { 75 if(l > r)return; 76 int mid = (l+r)/2; 77 NewNode(x,father,a[mid]); 78 Build(ch[x][0],l,mid-1,x); 79 Build(ch[x][1],mid+1,r,x); 80 push_up(x); 81 } 82 void Init() 83 { 84 root = tot1 = tot2 = 0; 85 ch[root][0] = ch[root][1] = size[root] = pre[root] = 0; 86 rev[root] = 0; 87 add[root] = 0; 88 NewNode(root,0,-1); 89 NewNode(ch[root][1],root,-1); 90 for(int i = 0;i < n;i++) 91 scanf("%d",&a[i]); 92 Build(Key_value,0,n-1,ch[root][1]); 93 push_up(ch[root][1]); 94 push_up(root); 95 } 96 //旋转,0为左旋,1为右旋 97 void Rotate(int x,int kind) 98 { 99 int y = pre[x]; 100 push_down(y); 101 push_down(x); 102 ch[y][!kind] = ch[x][kind]; 103 pre[ch[x][kind]] = y; 104 if(pre[y]) 105 ch[pre[y]][ch[pre[y]][1]==y] = x; 106 pre[x] = pre[y]; 107 ch[x][kind] = y; 108 pre[y] = x; 109 push_up(y); 110 } 111 void Splay(int r,int goal) 112 { 113 push_down(r); 114 while(pre[r] != goal) 115 { 116 if(pre[pre[r]] == goal) 117 { 118 push_down(pre[r]); 119 push_down(r); 120 Rotate(r,ch[pre[r]][0] == r); 121 } 122 else 123 { 124 push_down(pre[pre[r]]); 125 push_down(pre[r]); 126 push_down(r); 127 int y = pre[r]; 128 int kind = ch[pre[y]][0]==y; 129 if(ch[y][kind] == r) 130 { 131 Rotate(r,!kind); 132 Rotate(r,kind); 133 } 134 else 135 { 136 Rotate(y,kind); 137 Rotate(r,kind); 138 } 139 } 140 } 141 push_up(r); 142 if(goal == 0) root = r; 143 } 144 int Get_kth(int r,int k) 145 { 146 push_down(r); 147 int t = size[ch[r][0]] + 1; 148 if(t == k)return r; 149 if(t > k)return Get_kth(ch[r][0],k); 150 else return Get_kth(ch[r][1],k-t); 151 } 152 void ADD(int x) 153 { 154 //先搬移动 155 Splay(tp,0); 156 int tmp = size[ch[root][0]] + 1; 157 Splay(Get_kth(root,1),0); 158 Splay(Get_kth(root,tmp),root); 159 tmp = Key_value; 160 Key_value = 0; 161 push_up(ch[root][1]); 162 push_up(root); 163 Splay(Get_kth(root,size[root] - 1),0); 164 Key_value = tmp; 165 pre[Key_value] = ch[root][1]; 166 push_up(ch[root][1]); 167 push_up(root); 168 Splay(Get_kth(root,1),0); 169 Splay(Get_kth(root,k2+2),root); 170 Update_ADD(Key_value,x); 171 push_up(ch[root][1]); 172 push_up(root); 173 tp = Get_kth(root,2); 174 } 175 void REVERSE() 176 { 177 Splay(tp,0); 178 int tmp = size[ch[root][0]] + 1; 179 Splay(Get_kth(root,1),0); 180 Splay(Get_kth(root,tmp),root); 181 tmp = Key_value; 182 Key_value = 0; 183 push_up(ch[root][1]); 184 push_up(root); 185 Splay(Get_kth(root,size[root] - 1),0); 186 Key_value = tmp; 187 pre[Key_value] = ch[root][1]; 188 push_up(ch[root][1]); 189 push_up(root); 190 Splay(Get_kth(root,1),0); 191 Splay(Get_kth(root,k1+2),root); 192 Update_Rev(Key_value); 193 push_up(ch[root][1]); 194 push_up(root); 195 tp = Get_kth(root,2); 196 } 197 void INSERT(int x) 198 { 199 Splay(tp,0); 200 //printf("%d %d ",tp,size[ch[root][0]]+2); 201 int tt = Get_kth(root,size[ch[root][0]]+2); 202 //printf("%d %d %d ",Get_kth(root,size[ch[root][0]]+2),tt,key[tt]); 203 Splay(Get_kth(root,size[ch[root][0]]+2),root); 204 NewNode(Key_value,ch[root][1],x); 205 push_up(ch[root][1]); 206 push_up(root); 207 } 208 void DELETE() 209 { 210 Splay(tp,0); 211 int tmp = size[ch[root][0]] + 1; 212 Splay(Get_kth(root,tmp-1),0); 213 Splay(Get_kth(root,tmp+1),root); 214 s[++tot2] = Key_value; 215 Key_value = 0; 216 push_up(ch[root][1]); 217 push_up(root); 218 if(tmp == size[root])tp = Get_kth(root,2); 219 else tp = Get_kth(root,tmp); 220 } 221 int MOVE(int x) 222 { 223 if(x == 1) 224 { 225 Splay(tp,0); 226 int tmp = size[ch[root][0]] + 1; 227 tmp--; 228 if(tmp == 1)tmp = size[root] - 1; 229 tp = Get_kth(root,tmp); 230 } 231 else 232 { 233 Splay(tp,0); 234 int tmp = size[ch[root][0]] + 1; 235 tmp++; 236 if(tmp == size[root])tmp = 2; 237 tp = Get_kth(root,tmp); 238 //cout<<tp<<endl; 239 } 240 } 241 int query() 242 { 243 Splay(tp,0); 244 return key[root]; 245 } 246 char op[100]; 247 int x; 248 int main() 249 { 250 //freopen("in.txt","r",stdin); 251 //freopen("out.txt","w",stdout); 252 int iCase = 0; 253 while(scanf("%d%d%d%d",&n,&q,&k1,&k2) == 4) 254 { 255 if(n == 0 && q == 0 && k1 == 0 && k2 == 0)break; 256 iCase ++; 257 printf("Case #%d: ",iCase); 258 Init(); 259 tp = Get_kth(root,2); 260 while(q--) 261 { 262 scanf("%s",op); 263 if(op[0] == 'a') 264 { 265 scanf("%d",&x); 266 ADD(x); 267 } 268 else if(op[0] == 'r') 269 REVERSE(); 270 else if(op[0] == 'i') 271 { 272 scanf("%d",&x); 273 INSERT(x); 274 } 275 else if(op[0] == 'd') 276 DELETE(); 277 else if(op[0] == 'm') 278 { 279 scanf("%d",&x); 280 MOVE(x); 281 } 282 else printf("%d ",query()); 283 } 284 285 } 286 return 0; 287 }