HDU 4341 Gold miner（分组的背包问题）

Gold miner

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 454    Accepted Submission(s): 226

Problem Description

Homelesser likes playing Gold miners in class. He has to pay much attention to the teacher to avoid being noticed. So he always lose the game. After losing many times, he wants your help.

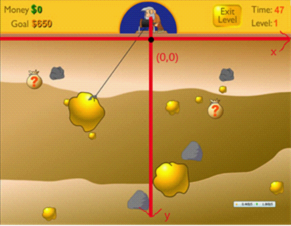
To make it easy, the gold becomes a point (with the area of 0). You are given each gold's position, the time spent to get this gold, and the value of this gold. Maybe some pieces of gold are co-line, you can only get these pieces in order. You can assume it can turn to any direction immediately.
Please help Homelesser get the maximum value.

 

Input

There are multiple cases.
In each case, the first line contains two integers N (the number of pieces of gold), T (the total time). (0＜N≤200, 0≤T≤40000)
In each of the next N lines, there four integers x, y (the position of the gold), t (the time to get this gold), v (the value of this gold). (0≤|x|≤200, 0＜y≤200,0＜t≤200, 0≤v≤200)

 

Output

Print the case number and the maximum value for each test case.

 

Sample Input

3 10 1 1 1 1 2 2 2 2 1 3 15 9 3 10 1 1 13 1 2 2 2 2 1 3 4 7

 

Sample Output

Case 1: 3 Case 2: 7

 

Source

2012 Multi-University Training Contest 5

 

Recommend

zhuyuanchen520

 

 

题意：一个人在原点（0，0）抓金子，每块金子有一个获得需要的时间t和价值v。而且有的金子可能在一条直线上，那只能先抓近的，再抓远的。求在给定时间T下，所能获得的最大价值。

 

这题可以转化为分组的背包问题。分组的背包问题详解见背包九讲。

先将所有点按照斜率排序，斜率相同按照距离排序。

然后进行分组，将斜率相同的分进同一个组。

比如有5个点1，2，3，4，5,6.

1斜率小，2，3斜率相同，4，5，6斜率相同。那分三组(1),(2,3),(4,5,6)

然后在同一个组内需要处理下。比如(2,3)是先要抓2才能抓3的。那就把2，3的t和v加起来给3。这样2，3就只能取一个了，就变成分组的背包问题了。

 

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;

const int MAXN=220;
struct Node
{
    int x,y;
    int v,t;
}node[MAXN];
bool cmp(Node a,Node b)//按照斜率从小到到排序，斜率相同按照距原点距离排序
{
    int x1=a.x;
    int y1=a.y;
    int x2=b.x;
    int y2=b.y;
    if(y1*x2==y2*x1)return y1<y2;
    return y1*x2<y2*x1;
}
int group[MAXN][MAXN];//group[i][0]表示第i组的总的点数,group[i][1-group[i][0]]就是该组点的编号
int cnt;//组数

int f[50000];
int solve(int T)
{
    memset(f,0,sizeof(f));//可以不装满的背包，初始化为0
    for(int i=0;i<cnt;i++)//对所有的组
      for(int t=T;t>=0;t--)
         for(int k=1;k<=group[i][0];k++)
         {
             if(t-node[group[i][k]].t>=0)
                f[t]=max(f[t],f[t-node[group[i][k]].t]+node[group[i][k]].v);
             //printf("%d %d\n",t,f[t]);
         }
    return f[T];
}
int main()
{
   // freopen("in.txt","r",stdin);
   // freopen("out.txt","w",stdout);
    int N,T;
    int iCase=0;
    while(scanf("%d%d",&N,&T)!=EOF)
    {
        iCase++;
        for(int i=0;i<N;i++)
          scanf("%d%d%d%d",&node[i].x,&node[i].y,&node[i].t,&node[i].v);
        sort(node,node+N,cmp);
        cnt=-1;

        for(int i=0;i<N;i++)
        {
            cnt++;
            group[cnt][0]=0;
            group[cnt][++group[cnt][0]]=i;
            int x1=node[i].x;
            int y1=node[i].y;
            int a=node[i].t;
            int b=node[i].v;

            for(i++;i<N;i++)
            {
                int x2=node[i].x;
                int y2=node[i].y;
                a+=node[i].t;
                b+=node[i].v;
                if(y1*x2==y2*x1)
                {
                    group[cnt][++group[cnt][0]]=i;
                    node[i].t=a;
                    node[i].v=b;
                }
                else {i--;break;}
            }
        }
        cnt++;

        //for(int i=0;i<N;i++)printf("%d %d\n",node[i].x,node[i].y);
        //for(int i=0;i<cnt;i++)printf("%d\n",group[i][0]);
        printf("Case %d: ",iCase);
        printf("%d\n",solve(T));
    }
    return 0;
}