POJ 3605 Sheryl's Circuit I

/*
题意：就是给你一个有2^n个输入的门电路，初始输入为全0，问至少要改变输入
开关多少次（即改变输入中0、1多少次）才能得到所需的0、1输出序列。

题意分析：

这道题的数据范围为k<10000，所以不能枚举暴搞，只能用递推来求解。

仔细分析就可一发现当有多个0或多个1在一起时，是不用改变开关的。只有
在输出序列中出现0到1或1到0的跳变时才需要改变开关。


*/

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int ch[10010];
char str[10010];
int n;
int solve(int i)//递归求从0变1需要的至少次数 
{
    if(2*i+1>=n-1)
    {
        if(ch[i]==0)return 1;
        else return 2;
    }    
    if(ch[i]==1) return solve(2*i+1)+solve(2*i+2);
    else return min(solve(2*i+1),solve(2*i+2));
}    
int main()
{
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        scanf("%s",&str);
        for(int i=0;i<n-1;i++)
        {
            scanf("%d",&ch[i]);
        }
        int m=solve(0);
        //printf("%d\n",m);
        int res;
        if(str[0]=='0') res=0;
        else res=1;
        int len=strlen(str);
        for(int i=1;i<len;i++)//找变化的次数，1变0，0变1 
        {
            if(str[i]!=str[i-1])res++;
        }        
        if(res)res+=m-1;//加上第一次变1 的次数，以后改变只需要一次就好了 
        printf("%d\n",res);
    }    
    return 0;
}
    

 

 

 

1A,好爽，去福州前去刷刷水题很痛快。。。。期待福州拿牌回来。。。

Sheryl's Circuit I

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1037		Accepted: 430

Description

In the Design of Digital Logic class, Sheryl is asked to design a device which can produce a digital signal (a sequence of 0 and 1), given by the professor. After several sleepless nights, she completes a kind of Boolean circuit which looks like a complete binary tree as showed in Figure 1. Every node of the tree is a Boolean arithmetic unit (BAU) which takes in inputs from its both children and produce an output to its parent. The inputs of BAU are either 1 or 0, and the output should be calculated due to the type of BAU which is either ∧ or ∨. The truth tables of the two types are also showed in Figure 1. The INPUT of Sheryl's circuit is the sequence of inputs of the lowest-level BAUs and the OUTPUT is the output of the top BAU.

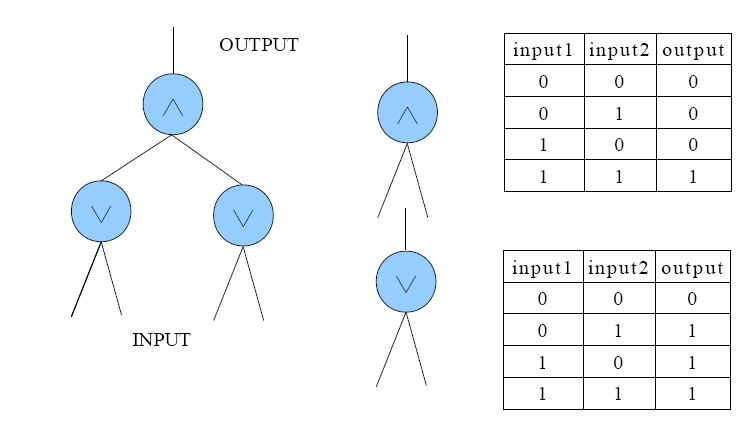
Figure 1

To accomplish the assignment, Sheryl has to manually handle the INPUT to produce the expected signal. For example, assuming Sheryl's circuit is the one showed in Figure 1, when the professor wants (0, 0, 0, 1, 1, 1) as the signal, the INPUT may alter as this: (0, 0, 0, 0) -> (0, 0, 1, 1) -> (1, 1, 0, 0) -> (1, 1, 1, 1) -> (1, 0, 1, 0) -> (0, 1, 0, 1). But this is too complex because Sheryl has to change the INPUT 14(2 + 4 + 2 + 2 + 4) times totally! So a more clever way is preferable, say (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 1, 0, 1) -> (0, 1, 0, 1) -> (0, 1, 0, 1), which requires only 2(0 + 0 + 2 + 0 +0) changes of the INPUT.

Given Sheryl's circuit and the signal expected, your task is to find the minimal changes of the INPUT to produce the signal. Note the INPUT begins with all 0s.

Input

There are multiple test cases.
The first line contains the number of test cases.
Each test case begins with an integer N( ≤ 10000), the number of inputs of Sheryl's circuit. It is guaranteed that N equals 2^k, where k is an integer.
The next line contains the expected signal which consists of 0 and 1 only. The length of the signal is no more than 10000.
Next N - 1 numbers describe the types of the BAUs, 0 for ∨ and 1 for ∧. The describing order is from top level to bottom level. For the same level it is from left to right.

Output

For each test case output the minimal number of changes in a separate line.

Sample Input

2
4
010101
0 0 0
4
111111
1 1 1

Sample Output

5
4

Source

POJ Founder Monthly Contest – 2008.06.29, Dagger

 

 

题意：就是给你一个有2^n个输入的门电路，初始输入为全0，问至少要改变输入开关多少次（即改变输入中0、1多少次）才能得到所需的0、1输出序列。

题意分析：

这道题的数据范围为k<10000，所以不能枚举暴搞，只能用递推来求解。

仔细分析就可一发现当有多个0或多个1在一起时，是不用改变开关的。只有在输出序列中出现0到1或1到0的跳变时才需要改变开关。