数列运算 题解

题目描述

在纸上有一个长为n的数列，第i项值为ai。

现在小A想要在这些数之间添加加号或乘号。问对于不同的 种方案，

所有答案的和是多少？

由于数据范围较大，所以输出对1000000007取模的结果。

输入格式

输入第一行一个整数n表示数列的长度。

之后一行n个整数，第n个整数表示数列的第i项ai。

输出格式

一行，答案对1000000007取模的结果。

样例输入

3
1 2 4

样例输出

30

数据范围与提示

对于30%的数据，1≤n≤10,1≤ai≤10^5

对于另外30%的数据，1≤n≤1000,ai=1

对于90%的数据，1≤n≤1000,1≤ai≤10^5

对于100%的数据，1≤100000,1≤ai≤10^9

分析

题目大意：如果有 n 个数，添加乘号或加号总共有 (2^{n-1}) 种方案，要求对其求和。

1. 首先想到暴搜，但是好像又不太好写，因为有加号有乘号的时候会先计算乘法，需要考虑的比较多，我是直接 pass 了。
2. 那就考虑递推呗。因为加法乘法混合的时候有优先级的问题，所以可以考虑如何巧妙的避开这个问题。我们可以考虑最后一个加号的位置，再之后所有的数之间都是做乘法，这样前后两部分相加就行了。顺着这个思想继续的话， 我们得考虑最后一个加号的位置，有 n 个数就会有 n-1 个位置，可以枚举一下。
   设 f[i] 表示 i 个数的总和，那么针对最后一个加号的位置，设最后一个加号在第 j 个数之后，那么有：
   (f[i] = sum_{j=1}^{i-1}(f[j]+a_{j+1} imes a_{j+2} imesdots imes a_i imes 2^{j-1}) + prod_{k=1}^i a_k)。
   我们一项一项来分析：

• 因为最后一个加号的位置为 a[j] 之后，所以前面的总和我是预先已经得到的 f[j]，为 (2^{j-1}) 种方案的和，剩下的还有 (a_{j+1}dots a_i) 的乘积，相当于在原来的 f[j] 的每种方案中都要加上这么一个乘积，总共加了 (2^{j-1}) 次。
• 对于不同的 j，我们求和即可表示所有的方案。
• 最后别忘了还有一种方案是所有的都是乘号。

我们把上面的式子展开一下：
(f[i] = sum_{j=1}^{i-1}f[j] + sum_{j=1}^{i-1} (a_{j+1} imes a_{j+2} imesdots imes a_i imes 2^{j-1}) + prod_{k=1}^i a_k)。
下面我们又可以显然了：

• 显然第一部分的求和是可以递推解决的，设为sum[i-1]
• 显然最后一部分的乘积也可以递推解决，记为 pi[i]
• 显然中间的部分不好看出来，那就写一下
  
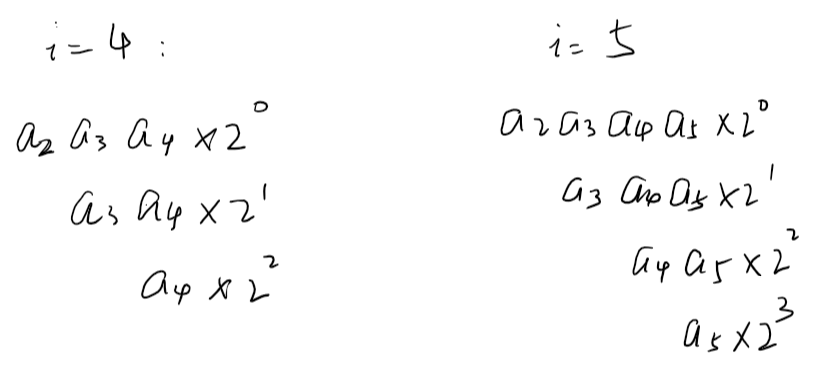
  对比 i = 4 和 i = 5 的时候，我们可以很容易找到递推式：
  设 s[i] 表示那一堆的和，那么：
  (s[i] = s[i-1] imes a[i] + a[i] imes 2^{i-2})
  因此我们就可以直接递推了：
  (f[i]=sum[i-1] + s[i] + pi[i])
  之后再更新一下 sum[i] 即可。