孟德尔随机化分析 Mendelian randomization,MR使用遗传变异作为工具变量,推断暴露因素与结局之间的因果关系,能有效克服混杂合反向因果问题所导致的偏倚。
1986年,Katan提出MR思想:由于配子形成时,遵循“亲代等位基因随机分配给子代”的孟德尔遗传规律,如果基因型决定表型,基因型通过表型而与疾病发生关联,因此可以使用基因型作为工具变量来推断表型与疾病之间的关联。
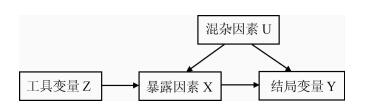
① 工具变量Z与混杂因素U无关联;② 工具变量Z与暴露因素X有关联;③ 工具变量Z与结局变量Y无关联,Z只能通过变量X与Y发生关联。
① 变量X与Y之间的关联一定会受到潜在混杂因素U的影响,但工具变量Z与变量X以及Z与变量Y之间无潜在混杂因素影响;② 变量X与结局Y之间的关联无法直接观察获得,因为无法直接测量变量X,但是Z是可测量的,并且Z与X直接的关联是已知的或者可测量的,并独立于其他因素而存在。(http://html.rhhz.net/zhlxbx/20170427.htm)
孟德尔随机化是在非实验数据中使用遗传变异来估计暴露和结局之间的因果关系,也称为“孟德尔解混杂”,它旨在给出因果关系的估计,不会因混杂因素而产生偏差。孟德尔随机化的想法是找到与暴露有关的遗传变异(或多个变异),但与影响结果的人和其他风险因素无关,并且与结果不直接相关。遗传变异与结果之间的任何关联都必须通过与暴露之间的关联来进行,因此暗示了暴露对结果的因果关系,这样的遗传变异将满足工具变量(IV)的假设
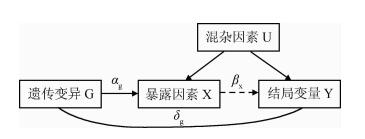
孟德尔随机中,遗传变异被作为工具变量评估暴露对结局的因果效应,遗传变异满足工具变量的基本条件总结为:
1)遗传变异与暴露有关。
2)遗传变异与暴露-结果关联的任何混杂因素均不相关
3)改遗传变异不会影响结果,除非可能通过化瘀暴露的关联来实现。
尽管孟德尔随机化分析通常涉及单个遗传变异,但可以将多个变异用作单独的IV或组合为单个IV。
暴露:指假定的因果风险因素,有时称为中间表型,它可以是生物标志物(Biomarker)、人体测量指标(Physical measurement)或任何其他影响结果的风险因素(Risk factor)。通常,结局是疾病,但不局限于疾病。
非实验数据涵盖了所有观察性研究,包括横断面和纵向,队列研究和病例对照研究。
流行病学研究的基本目标是估计暴露对结局的影响
通常由于混杂因素,暴露与结果之间的观察联系有所不同,它们之间的相关性不能作为解释因果关系的可靠证据。
MR设计策略:随着统计学方法的深入不断更新,一阶段MR到单一样本MR,两样本MR,两阶段MR,双向MR以及基因-环境交互作用MR和网络额MR。
两样本MR在全球大量GWAS合作组的公共数据中广泛使用。两样本MR的设计策略是建立在G-X和G-Y的关联研究人群来自相同人群的两个独立样本(如GWAS与暴露,GWAS与结局的关联数据),要求两样本具有相似的年龄、性别和种族分布特征,因为样本量较大,该方法可以获得更大的把握度。
代码:# install package
if (!requireNamespace("MendelianRandomization"))
install.packages("MendelianRandomization")
library(MendelianRandomization)
IVWObject <- mr_ivw(MRInputObject,
model = "default",
robust = FALSE,
penalized = FALSE,
correl = FALSE,
weights = "simple",
psi = 0,
distribution = "normal",
alpha = 0.05)
IVWObject <- mr_ivw(mr_input(bx = ldlc, bxse = ldlcse,
by = chdlodds, byse = chdloddsse))
IVWObject

参考:
https://www.jianshu.com/p/354f9f0b9eed
http://html.rhhz.net/zhlxbx/20200813.htm
解释变量explanatory variable也称为可控制变量,即自变量。
随机误差项 random error term 也称为随机误差,不包含在模型中的解释变量或其他一些随机因素对被解释变量的总影响项。
工具变量 instrumental variable,简称“IV”,也称为辅助变量,在无法实现可控实验时,用于估计模型因果关系。在回归模型中,当解释变量与误差项存在相关性,使用工具变量能得到一致的估计量。工具变量应该是不属于原解释方程且与内生解释变量相关的变量。工具变量与所属随机解释变量高度相关,与随机误差项不相关;与模型中其他解释变量不相关;同一模型中需引入多个工具变量时,这些工具变量之间不相关。
弱工具变量:当遗传变异与暴露因素不具有强相关关系,或者遗传变异仅能解释小部分的表型变异时,研究者称之为“弱工具变量”。弱工具变量可导致统计学检验效能的降低,并且违背其他核心假设(例如遗传变异的多效性)所产生的偏倚将可能被放大[12]。为降低弱工具变量导致的偏倚,可采取以下两种策略:一是增加研究样本量。工具变量与暴露因素的关联强度通常使用回归模型中的F统计量加以评估。根据经验,工具变量的F统计量应>10[13]。由于F统计量受样本量的影响,使用公开GWAS或者GWAS汇总数据以增加样本量是减少弱工具变量偏倚的方法之一。二是增加表型解释度。相比于单个遗传变异,多个遗传变异能够解释更大比例的表型变异。通过构建等位基因评分(也称为遗传风险评分)以综合多个遗传变异的效应,将其作为工具变量来预测危险因素的暴露水平,能够增加工具变量所解释的表型变异、降低弱工具变量偏倚。
本研究采用逆方差加权法(IVW)[23]作 为首要的因果效应估计。IVW 法是一种较为理想状态 下的估计,是假设在所有遗传变异都是有效工具变量的 基本前提下进行的有效分析,具有较强的因果关系检测 能力。但是 IVW 法特别要求遗传变异仅通过研究中的 暴露影响目标结局。尽管此研究已尽可能排除了已知 的混杂的 SNP,然而仍然有许多未知混杂因素会导致基 因多效性并对效应值的估计产生偏倚。因此,我们采用 了另外 4 种方法来检验结果的可靠性和稳定性,即 MR- Egger 回归[24]、加权中位数法(WME)[25]、基于众数的简 单估计[26]、基于众数的加权估计[26]。依次对每个代谢物 进行 MR 分析,如果以上五种不同的 MR 模型对因果效 应产生了相似的估计值,我们则认为该代谢物与冠心病 的因果关系是稳定且可靠的。(两样本孟德尔随机化方法分析血液代谢物与冠心病的因果关系)
连锁不平衡分析采用 PLINK(version 1.9)软件;MR分析、基因多效性检验 以及敏感性分析采用 R 中的 TwoSampleMR 软件包
(version 0.4.22)于Linux系统上进行分析。
基因多效性检验 MR 分析的假设之一是工具变 量只能通过暴露影响结局,若工具变量不通过影响暴露 而直接影响结局则违背了 MR 思想,所以需要检验暴露 与结局之间的因果推断是否存在基因多效性。采用MR-Egger 回归分析可以来评价基因多效性产生的偏 倚,其回归截距可以评估多效性的大小,截距越接近于 0,则基因多效性的可能性越小
MR 可靠性评价:
1)敏感度分析:检测并剔除非特异性的作为工具变量的SNPs
2)MR-Egger回归分析:评价基因多效性带来的偏倚,MR-Egger回归直线的斜率可以估计定向多效性的大小。
MR研究的局限性:
1)难以发现合适的遗传工具变量:基于GWAS的GRS(genetic risk scores,遗传风险评分)并不很好,很难控制弱工具变量偏倚
2)把握度低:需要扩大样本量才能获得足够的把握度,比如使用仅占1%效应的遗传工具探讨暴露和疾病之间的关联,需要至少9500对以上的病例和对照样本才能有80%的把握度获得增加50%(OR=1.5)的生物学效应
3)Beavis效应:基于GWAS数据的MR研究可能会高估了遗传和暴露之间的关联,因为SNPs与混杂因素之间可能有潜在的关联。
4)合理的生物学校解释,尽管MR在因果推断中发挥重要作用,但并不完善。