部分内容
E-Knapsack2（背包dp）
容量w数据太大，dp数组改为f[v]即价值为v时的最小重量
转移方程f[j]=min(f[j],f[j-v[i]]+w[i])
F-LCS(最长公共子序列字符串版）
f[i][j]为两字符串前i、j个的最长公共子序列
并用book数组标记，book[i][j]=0表示状态由f[i-1][j]转移过来
book[i][j]=1表示状态由f[i][j-1]转移过来
book[i][j]=2表示第i、j个可以匹配，由f[i-1][j-1]转移过来
作用是dfs得到答案字符串
G-Longest Path（非dp）
链前存图，顺便统计个数入度
从没有入度的点开始遍历，队列实现
遍历过的入度减1，无入度时存入队列，此时该点已找到最大值
I - Coins(概率dp)
记f[i][j]为掷i次，j次向上的概率
则有f[i][j]=f[i-1][j-1]*p[i]+f[i-1][j]*(1.0-p[i]);
J - Sushi
在DFS中设a为1个盘子的数量，b为2个的数量，c为3个
最后一次一定是a=1,b=0,c=0
由该状态递推，每一次操作期望为（总操作数/有效操作数）
double tot=0;
if(a) tot+=dfs(a-1,b,c)*(1.0*a/(a+b+c));
if(b) tot+=dfs(a+1,b-1,c)*(1.0*b/(a+b+c));
if(c) tot+=dfs(a,b+1,c-1)*(1.0*c/(a+b+c));
tot=tot+1.0*n/(a+b+c);
return f[a][b][c]=tot;
K - Stones（博弈论）
给出n种取法a[i]，k为上限，先不能取的人就输，t=0即以A为主观，1即以B为主观
从结果k往前推，以先取的人(A)为主观
将k-a[i]能够到的数字记为后取的人(B)的必胜点
如果B达不到，则A能胜
所以再往前A要达到让B不能达到的点
以此类推
if(k>=a[i]&&!dfs(k-a[i],!t))
{xx=true;}
L-Deque（绝世dp）
题目要求在a数组双端不断取数，Taro取值总和为X，Jiro取值总和为Y
Taro试图最大化X-Y，Jiro最小化X-Y
则两人都想取尽可能大的数
将Jiro转变为最大化Y-X
上一个人取的最大值在下一个状态变成相反数
就有f[l][r]=max(a[l]-f[l+1][r],a[r]-f[l][r-1])
M-Candies
统计糖果分配方法个数，每人取值上限为a[i]
f[i][j]为前i个人已经分了j颗糖的方案数
遍历过后把f[i][j]变为f[i][1-j]的前缀和，方便计算
方程f[i][j]=f[i-1][j]-f[i-1][j-a[i]-1]
N - Slimes
常规区间dp，
在每一对l和r中间枚举断点求最值
O - Matching（状压dp）
写个for(int i=0;i<(1<<n);++i)在外面表示男生匹配的状态
设f[s]表示匹配好的女生的状态为s（二进制表示s）
if(m[num][j]==1&&((1<<j)^i)!=i)可以配对但还没转移=>f[(1<<j)^i]=(f[(1<<j)^i]+f[i])%Mod;
P - Independent Set（简单树形dp）
f[i][0]和f[i][1]存方案
子节点方案乘起来
Q - Flowers（上升子序列附加值）
对于每个i有高度h[i]和值a[i]，设f[i]表示1-i的上升子序列最大值
以h[i]为下标存入树状数组，每更新一个i先求出f[i]=a[i]+max(pre[h[1~i]])
之后在update(h[i],f[i])
最后ans=max(f[i])
R - Walk(矩阵乘法）
矩阵乘法在图中的应用（结论题）
矩阵A的n次幂表示走n次x到y的方案数，求矩阵的k次幂，再求结果矩阵上各个点上的和
S - Digit Sum（数位dp模板）
ll dfs(int x,int p,bool limit){ if(x==0) return p?0:1; if(f[x][p]!=-1&&!limit) return f[x][p]; ll ans=0; int up=limit?num[x]:9; for(int i=0;i<=up;++i){ ans=(ans+dfs(x-1,(p+i+d)%d,limit&&(i==up)))%Mod; } if(!limit) f[x][p]=ans; return ans; } int main(){ scanf("%s",s+1); scanf("%lld",&d); n=strlen(s+1); for(int i=1;i<=n;++i){ num[n-i+1]=s[i]-'0'; } memset(f,-1,sizeof(f)); ll ans=dfs(n,0,true); printf("%lld ",(ans-1+Mod)%Mod); return 0; }
up表示该位置的数字上限，如25，十位为1时个位up=9，十位为2时limit=true，个位上up=5
T - Permutation（较难）
f[i][j]表示在前i个中，第i个从小到大排名为j的情况
如果当前符号为小于号，则f[i][j]由f[i-1][1~j-1]转化来
如果当前符号为大于号，则f[i][j]由f[i-1][j~i]转化来
并用pre数组前缀和维护
int main(){ scanf("%d %s",&n,s+1); f[1][1]=1; for(int i=1;i<=n;++i){ pre[1][i]=1; } for(int i=2;i<=n;++i){ for(int j=1;j<=i;++j){ if(s[i-1]=='>')f[i][j]=(f[i][j]+pre[i-1][i]-pre[i-1][j-1]+Mod)%Mod; else f[i][j]=(f[i][j]+pre[i-1][j-1])%Mod; } for(int j=1;j<=n;++j){ pre[i][j]=(pre[i][j-1]+f[i][j])%Mod; } } ll ans=0; for(int i=1;i<=n;++i){ ans=(ans+f[n][i])%Mod; } printf("%lld ",ans); return 0; }
U - Grouping（状压dp）
思维容易，难在实现
先求出各种分组的情况，再由多个小组的min向大组转化
如0001、0010....=>0011,0101,0110....=>.....=>1111(有点区间思想）
ll que(int now){ ll tot=0; for(int i=1;i<=n;++i){ for(int j=1;j<i;++j){ if(((1<<(i-1))&now)&&(((1<<(j-1))&now))) tot+=a[i][j]; } } return tot; } int main(){ scanf("%lld",&n); int S=(1<<n)-1; for(int i=1;i<=n;++i){ for(int j=1;j<=n;++j){ scanf("%lld",&a[i][j]); } } for(int i=1;i<=S;++i){ c[i]=que(i); } for(int i=1;i<=S;++i){ for(int j=i;j>=0;j=(i&(j-1))){ f[i]=max(f[i],f[j]+c[i^j]); if(j==0) break; } } printf("%lld",f[S]); return 0; }
V - Subtree（染色类问题）（换根dp）
由于换根，i点往上往旁子树走的设为f[i][1]，往下的为f[i][0]
从根往叶子结点dfs，遍历当前点默认涂黑，所以f数组初始化为1
子节点方案算完后记得自己加上1，即自己和子树全部涂白的方案
最后输出up[i]*down[i]时注意down[i]-1,默认自己为黑
void dp(int u,int fa){ for(int i=0;i<v[u].size();i++){ int to=v[u][i]; if(fa==to) continue; dp(to,u); f[u][0]=f[u][0]*f[to][0]%mod; } f[u][0]++; } void query(int u,int fa){ ll num=f[u][1];int siz=v[u].size(); for(int i=0;i<siz;i++){ int to=v[u][i]; if(to==fa) continue; f[to][1]=f[to][1]*num%mod; num=num*f[to][0]%mod; } num=1; for(int i=siz-1;i>=0;--i){ int to=v[u][i]; if(to==fa) continue; f[to][1]=f[to][1]*num%mod; num=num*f[to][0]%mod; } for(int i=0;i<siz;++i){ int to=v[u][i]; if(to==fa) continue; f[to][1]++; query(to,u); } } int main(){ scanf("%lld %lld",&n,&mod); for(int i=1;i<=n;++i){ f[i][0]=f[i][1]=1; } for(int i=1;i<n;++i){ int a,b; scanf("%d %d",&a,&b); v[a].push_back(b); v[b].push_back(a); } dp(1,0); query(1,0); for(int i=1;i<=n;++i){ printf("%lld ",((f[i][1])*(f[i][0]-1))%mod); } return 0; }
W - Intervals（线段树优化dp）
区间先按r排序
从1到n枚举时先默认这里是0，update单点为前面的最大值
如果到了边界就直接为1，更新一个新的结果，即每个结果依附在区间上面
最后查找整个序列里面最大的结果，将他输出
#include <iostream> #include <cstdio> #include <algorithm> #define ll long long #define int long long const int Maxn=2e5+10; using namespace std; struct Node{ ll l,r,v; }p[Maxn]; struct Node1{ ll l,r,v,laz; }tr[Maxn<<2]; ll n,m; bool cmp(Node x,Node y){ return x.r<y.r; } void push_up(ll m){ tr[m].v=max(tr[m<<1].v,tr[m<<1|1].v); } void push_down(ll m){ if(tr[m].laz){ tr[m<<1].laz+=tr[m].laz; tr[m<<1|1].laz+=tr[m].laz; tr[m<<1|1].v+=tr[m].laz; tr[m<<1].v+=tr[m].laz; tr[m].laz=0; } } void build(ll m,ll l,ll r){ ll mid=(l+r)>>1; tr[m].l=l; tr[m].r=r; if(l==r) return ; build(m<<1,l,mid); build(m<<1|1,mid+1,r); } void update(int m,int l,int r,int v,int sign){ if(tr[m].l>r||tr[m].r<l) return ; if(l<=tr[m].l&&tr[m].r<=r){ if(sign){ tr[m].v+=v; tr[m].laz+=v; } else tr[m].v=v; return ; } push_down(m); update(m<<1,l,r,v,sign); update(m<<1|1,l,r,v,sign); push_up(m); } int query(int m,int l,int r){ if(tr[m].l>r||tr[m].r<l) return 0; if(l<=tr[m].l&&tr[m].r<=r) return tr[m].v; push_down(m); return max(query(m<<1,l,r),query(m<<1|1,l,r)); } signed main(){ scanf("%lld %lld",&n,&m); for(ll i=1;i<=m;++i){ scanf("%lld %lld %lld",&p[i].l,&p[i].r,&p[i].v); } sort(p+1,p+m+1,cmp); build(1,1,n); int tot=1; for(ll i=1;i<=n;++i){ update(1,i,i,query(1,1,i-1),0); while(p[tot].r==i){ update(1,p[tot].l,p[tot].r,p[tot].v,1); tot++; } } printf("%lld",max(0ll,tr[1].v)); return 0; }
X - Tower（贪心+01背包）
核心在于排序
假设两个物品 w1,s1分别有w2,s2,如果第一个物品在上面，那么还能放的重量为s2-w1,反之就是s1-w2。
如果s2-w1>s1-w2，即s2+w2>s1+w1,价值一样的情况下，第一个物品放上面肯定优。
那么对s+w按照升序排序，综合s+w大的的选择放下面，变成01背包问题。
bool cmp(Node x,Node y){ return x.s+x.w<y.s+y.w;//s+w大的放下面，排序后从上往下搜 } int main(){ scanf("%d",&n); for(int i=1;i<=n;++i){ scanf("%d %d %d",&b[i].w,&b[i].s,&b[i].v); } sort(b+1,b+n+1,cmp); for(int i=1;i<=n;++i){ for(int j=b[i].s;j>=0;--j){//上面的已经dp过，j要小于s f[j+b[i].w]=max(f[j+b[i].w],f[j]+b[i].v); } } ll ans=0; for(int i=1;i<=100010;++i){ ans=max(ans,f[i]); } printf("%lld",ans); return 0; }
Y - Grid 2（数论dp）
假设（1,1）~（n,m）无障碍
那么方案数就为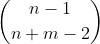
那么第1、2个障碍(x1,y1),(x2,y2)间就少了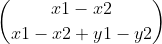
*
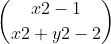种情况(x2<x1且y2<y1)
不断往终点推过去
组合数乘法用到（费马小定理求逆元）
ll mm(ll x,ll y){ ll ans=1; while(y){ if(y&1) ans=(ans*x)%Mod; y>>=1; x=(x*x)%Mod; } return ans; } ll C(ll x,ll y){ if(x<y) return 0; return ((jiec[x]*(mm(jiec[x-y],Mod-2)%Mod))%Mod*(mm(jiec[y],Mod-2)%Mod))%Mod; } bool cmp(Node b,Node c){ if(b.x==c.x) return b.y<c.y; return b.x<c.x; } int main(){ scanf("%lld %lld %lld",&h,&w,&n); for(ll i=1;i<=n;++i){ scanf("%lld %lld",&a[i].x,&a[i].y); } jiec[0]=1; for(ll i=1;i<=1e6;++i) jiec[i]=(jiec[i-1]*i)%Mod; n++; a[n].x=h,a[n].y=w; sort(a+1,a+n+1,cmp); for(ll i=1;i<=n;++i){ ll now=C(a[i].x+a[i].y-2,a[i].x-1)%Mod; for(ll j=1;j<i;++j){ if(a[j].y<=a[i].y){ ll xx=a[i].x-a[j].x+1; ll yy=a[i].y-a[j].y+1; now=(now-f[j]*C(xx+yy-2,xx-1)%Mod+Mod)%Mod; } } f[i]=now; } printf("%lld",f[n]%Mod); return 0; }
Z - Frog 3（斜率优化dp）
高级人的算法
一个重点是截距有区分正负
https://blog.csdn.net/mrcrack/article/details/88252442
https://www.luogu.com.cn/blog/Garyhuang1234567890/solution-at4547
两个博客就可以掌握
double X(ll i){ return h[i]; } double Y(ll i){ return f[i]+h[i]*h[i]; } double K(ll i,ll j){ return (Y(j)-Y(i))/(X(j)-X(i)); } int main(){ scanf("%lld %lld",&n,&c); for(ll i=1;i<=n;++i){ scanf("%lld",&h[i]); } f[1]=0; q[++head]=1; tail=1; for(ll i=2;i<=n;++i){ while(head<tail&&h[i]*2>=K(q[head],q[head+1])) head++; f[i]=(h[q[head]]-h[i])*(h[q[head]]-h[i])+f[q[head]]+c; while(head<tail&&K(q[tail],i)<=K(q[tail],q[tail-1])) tail--; q[++tail]=i; } printf("%lld",f[n]); return 0; }