顺序表和链表和二叉树

顺序表和链表

顺序表

• 集合中存储的元素是有顺序的，顺序表的结构可以分为两种形式：单数据类型和多数据类型。
• python中的列表和元组就属于多数据类型的顺序表

 

• 单数据类型顺序表的内存图（内存连续开启）
  • 对应的内存空间是连续开辟的
  • 顺序表的变量/引用存的的（指向的）是内存空间的首地址

 

• 多数据类型顺序表的内存图（内存非连续开辟）

重点:

• 想把数据存储到内存中，必须先在内存中开辟指定大小的内存空间（大小，地址：定位
• 如果一个引用指向了某一块内存空间，则表示该引用存储了该内存空间的地址

 

• 顺序表的弊端：顺序表的结构需要预先知道数据大小来申请连续的存储空间，而在进行扩充时又需要进行数据的搬迁。

链表: 相对于顺序表，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理且进行扩充时不需要进行数据搬迁。

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是每一个结点（数据存储单元）里存放下一个结点的信息（即地址）

. is_empty()：链表是否为空

. length()：链表长度

. travel()：遍历整个链表

. add(item)：链表头部添加元素

. append(item)：链表尾部添加元素

. insert(pos, item)：指定位置添加元素

. remove(item)：删除节点

. search(item)：查找节点是否存在

#封装节点数据结构
class Node():
    def __init__(self,item):
        self.item = item
        self.next = None
    def __str__(self):
        return self.item
#封装链表数据结构
class Link():
    #初始化一个空链表
    def __init__(self):
        #该属性永远指向第一个节点
        self._head = None
    def isEmpty(self):
        return self._head == None
    def add(self,item):
        #创建一个新的节点对象
        node = Node(item)
        #将节点插入到链表的头部
        node.next = self._head
        self._head = node
    def travel(self):
        cur = self._head
        while cur:
            print(cur.item)
            cur = cur.next
    def length(self):
        count = 0
        cur = self._head
        while cur:
            count += 1
            cur = cur.next
        return count
    def append(self,item):
        cur = self._head
        pre = None #cur前面节点的地址
        
        node = Node(item)
        #如果链表为空则新节点作为链表中的第一个节点
        if self._head is None:
            self._head = node
            return
        #链表非空对应的插入情况    
        while cur:
            pre = cur
            cur = cur.next
        pre.next = node
      
    def insert(self,pos,item):
        cur = self._head
        pre = None
        node = Node(item)
        length = self.length()
        #对特殊情况的处理
        if pos > length:
            self.append(item)
            return
        if pos <= 0:
            self.add(item)
            return
        #正常处理
        for i in range(pos):
            pre = cur
            cur = cur.next
        pre.next = node
        node.next = cur
    def remove(self,item):
        cur = self._head
        pre = None
        #如果删除的是第一个节点
        if item == cur.item:
            self._head = cur.next
            return
        while cur:
            if cur.item == item:
                pre.next = cur.next
                return
            else:
                pre = cur
                cur = cur.next
        
        
    def search(self,item):
        find = False
        cur = self._head
        while cur:
            if cur.item == item:
                find = True
                break
            cur = cur.next
        return find

link = Link()
link.add(10)
link.add('aa')
link.append('bobo')
link.append('bobo1')
link.insert(111,666)
# link.remove('aa')
link.travel()
print(link.length())
link.search(6669)

aa
10
bobo
bobo1
666
5

Out[36]:False

 二叉树

• 根节点
• 左叶子节点
• 右叶子节点
• 子树

class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None
class Tree():
    def __init__(self):
        self.root = None
    def add(self,item):
        node = Node(item)
        
        if self.root is None:
            self.root = node
            return       
        queue = [self.root]
        while queue:
            cur = queue.pop(0)
            if cur.left is None:
                cur.left = node
                return
            else:
                queue.append(cur.left)
            if cur.right is None:
                cur.right = node
                return
            else:
                queue.append(cur.right)
    def travel(self):
        if self.root is None:
            return
        queue = [self.root]
        
        while queue:
            cur = queue.pop(0)
            print(cur.item)
            if cur.left is not None:
                queue.append(cur.left)
            if cur.right is not None:
                queue.append(cur.right)

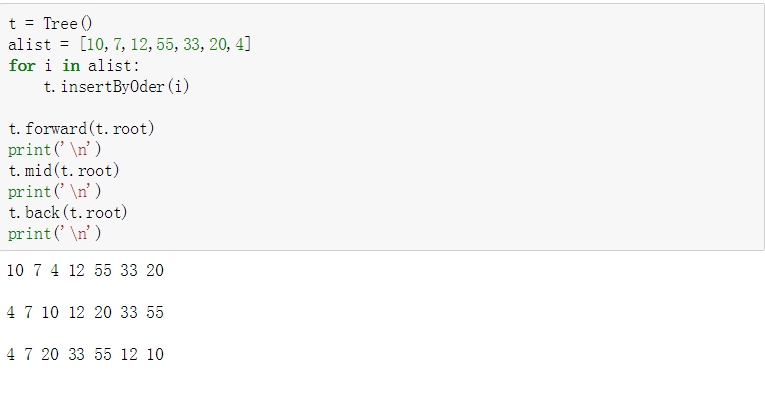
 实现排序二叉树

class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None
class Tree():
    def __init__(self):
        self.root = None
        
    def insertByOder(self,item):
        
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        
        cur = self.root
        while True:
            if item < cur.item:
                if cur.left is None:
                    cur.left = node
                    return
                else:
                    cur = cur.left
            else:
                if cur.right is None:
                    cur.right = node
                    return
                else:
                    cur = cur.right
            
    def forward(self,root):
        if root is None:
            return
        # 根 左 右
        print(root.item,end=' ')
        self.forward(root.left)
        self.forward(root.right)
    def mid(self,root):
        if root is None:
            return
        #左根右
        self.mid(root.left)
        print(root.item,end=' ')
        self.mid(root.right)
    def back(self,root):
        if root is None:
            return
        #左右根
        self.back(root.left)
        self.back(root.right)
        print(root.item,end=' ')