题意:
给你一个由n个点,n-1条有向边构成的一颗树,1为根节点
下面会输入n-1个数,第i个数表示第i+1点的父节点。你可以去添加一条边(你添加的边也是有向边),然后找出来(x,y)这样的成对节点。问你最多能找出来多少对
其中x和y可以相等,且x点要可以到达y点
题解:
根据样例找一下就可以看出来让根节点1和深度最深那个点相连之后能找出来的(x,y)最多
但是又出现一个问题,如果那个最大深度的点不止一个,那么我们要选择那个。如下样例
6
1 1 2 2 3
化成图就是
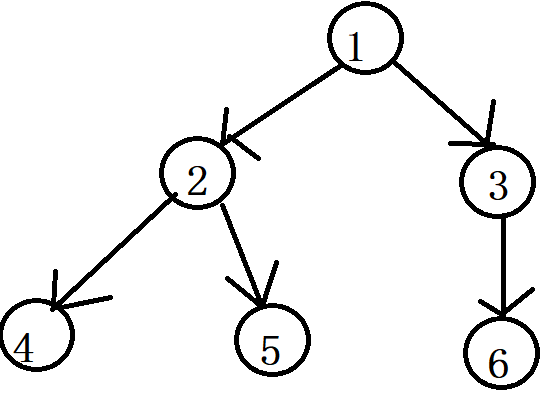
4、5、6号点都是最深深度的点,且如果你选择4或5和根节点1相连,那么(x,y)的数量是22,如果你选择6点和根节点1相连,那么(x,y)的数量是23
所以最深深度节点有多个我们还需要判断,于是我们先找到所有最深深度的点,然后对它们进行枚举
设最深深度为maxx,你会发现,答案的一部分是maxx*(n-1)+maxx
maxx*(n-1):就是我们找到的那个最深深度那个点和根节点1构成的那个链,那个链上的所有点都可以到达其他顶点,所以就是这个答案
maxx:因为x和y可以相等,所以就加上这个链上的所有点
对于其他(x,y)我么可以这样找,我们还用上面的例子,我们找最长链为1,3,6
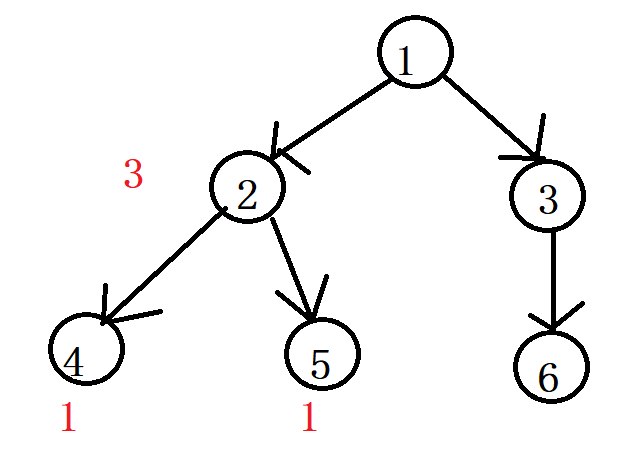
我们首先把1,3,6这条边标记,然后把没有标记链的红色权值加起来就行了,红色权值的构成就是每一个点最开始红色权值是1,然后子节点为父节点贡献它的权值,子节点向父节点贡献权值就相当于(2,4)和(2,5)。
它们本身最开始的权值1就相当于(4,4),(5,5),(2,2)
但是最后你会发现这样会TLE
TLE代码:

1 #include<stack> 2 #include<queue> 3 #include<map> 4 #include<cstdio> 5 #include<cstring> 6 #include<iostream> 7 #include<algorithm> 8 #include<vector> 9 #define fi first 10 #define se second 11 #define pb push_back 12 using namespace std; 13 typedef long long ll; 14 const int maxn=5e5+10; 15 const int mod=1e9+7; 16 const double eps=1e-8; 17 ll vis[maxn],val[maxn],fa[maxn],test[maxn],head[maxn],summ[maxn]; 18 queue<ll>r; 19 vector<ll>w[maxn]; 20 void add_edge(ll x,ll y) 21 { 22 w[x].push_back(y); 23 } 24 void dfs(ll x) 25 { 26 ll len=w[x].size(); 27 for(ll i=0;i<len;++i) 28 { 29 ll y=w[x][i]; 30 dfs(y); 31 summ[x]+=summ[y]; 32 } 33 } 34 int main() 35 { 36 ll t; 37 scanf("%lld",&t); 38 while(t--) 39 { 40 while(!r.empty()) 41 r.pop(); 42 memset(vis,0,sizeof(vis)); 43 memset(test,0,sizeof(test)); 44 ll n,x,total,maxx=1,pos=1,index=1; 45 scanf("%lld",&n); 46 for(int i=1;i<=n;++i) 47 w[i].clear(); 48 fa[1]=0; 49 val[1]=1; 50 summ[1]=1; 51 for(ll i=2; i<=n; ++i) 52 { 53 summ[i]=1; 54 scanf("%lld",&fa[i]); 55 add_edge(fa[i],i); 56 val[i]=val[fa[i]]+1; 57 test[fa[i]]=i; 58 if(maxx<val[i]) 59 { 60 maxx=val[i]; 61 pos=i; 62 } 63 } 64 dfs(1); 65 // for(ll i=2; i<=n; ++i) 66 // { 67 // if(test[i]==0) 68 // { 69 // head[index++]=i; 70 // ll temp=i; 71 // while(fa[temp]) 72 // { 73 // summ[fa[temp]]+=summ[temp]; 74 // temp=fa[temp]; 75 // } 76 // } 77 // } 78 for(ll i=2; i<=n; ++i) 79 { 80 if(val[i]==maxx) 81 { 82 r.push(i); 83 } 84 } 85 ll result=0; 86 ll bloo=maxx*(n-1)+maxx; 87 //printf("%d %lld ",r.size(),maxx*(n-1)+n); 88 while(!r.empty()) 89 { 90 ll temp=r.front(),sum=bloo; 91 while(temp) 92 { 93 vis[temp]=1; 94 temp=fa[temp]; 95 } 96 temp=r.front(); 97 for(ll i=2;i<=n;++i) 98 { 99 if(vis[i]==0) 100 { 101 sum+=summ[i]; 102 // if(temp==8) 103 // { 104 // printf("%lld %lld ",i,summ[i]); 105 // } 106 } 107 108 } 109 result=max(result,sum); 110 temp=r.front(); 111 r.pop(); 112 while(temp) 113 { 114 vis[temp]=0; 115 temp=fa[temp]; 116 } 117 } 118 printf("%lld ",result); 119 } 120 return 0; 121 } 122 /* 123 124 */
然后就想办法优化,你可以先把所有节点的红色权值都算出来,然后把这些值都加起来,使用变量k保存,然后我们用一个数组变量
sumi表示从根节点到i节点所有节点红色权值的和
对于我们枚举到的一个最深深度节点i,我们可以使用k-sum[i]来找出来排除最长链之外的其他点能找到的(x,y)
然后再加上之前的maxx*(n-1)+maxx就行了
AC代码:
1 #include <cstdio> 2 #include <algorithm> 3 #include <iostream> 4 #include <vector> 5 #include <map> 6 #include <queue> 7 #include <set> 8 #include <ctime> 9 #include <cstring> 10 #include <cstdlib> 11 #include <math.h> 12 using namespace std; 13 typedef long long ll; 14 const ll N = 2009; 15 const ll maxn = 1e6 + 20; 16 const ll mod = 1000000007; 17 ll inv[maxn], vis[maxn], dis[maxn], head[maxn], dep[maxn], out[maxn]; 18 ll fac[maxn], a[maxn], b[maxn], c[maxn], pre[maxn], cnt, sizx[maxn]; 19 vector<ll> vec; 20 char s[maxn]; 21 ll sum[maxn]; 22 ll max(ll a, ll b) { return a > b ? a : b; } 23 ll min(ll a, ll b) { return a < b ? a : b; } 24 ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; } 25 ll lcm(ll a, ll b) { return a * b / gcd(a, b); } 26 map<ll, ll> mp; 27 ll ksm(ll a, ll b) 28 { 29 a %= mod; 30 ll ans = 1ll; 31 while (b) 32 { 33 if (b & 1) 34 ans = (ans * a) % mod; 35 a = (a * a) % mod; 36 b >>= 1ll; 37 } 38 return ans; 39 } 40 ll lowbit(ll x) 41 { 42 return x & (-x); 43 } 44 ll dp[maxn][3]; 45 queue<int> q; 46 struct node 47 { 48 ll v, nex; 49 } edge[maxn << 1]; 50 void add(ll u, ll v) 51 { 52 edge[cnt].v = v, edge[cnt].nex = head[u]; 53 head[u] = cnt++; 54 } 55 void dfs1(ll u, ll fa) 56 { 57 dep[u] = dep[fa] + 1; 58 sizx[u] = 1ll; 59 for (ll i = head[u]; ~i; i = edge[i].nex) 60 { 61 ll v = edge[i].v; 62 if (v != fa) 63 { 64 dfs1(v, u); 65 sizx[u] += sizx[v]; 66 } 67 } 68 } 69 void dfs2(ll u, ll fa) 70 { 71 sum[u] = sum[u] + sum[fa] + sizx[u]; 72 for (ll i = head[u]; ~i; i = edge[i].nex) 73 { 74 ll v = edge[i].v; 75 if (v != fa) 76 dfs2(v, u); 77 } 78 } 79 int main() 80 { 81 ll t; 82 scanf("%lld", &t); 83 while (t--) 84 { 85 vec.clear(); 86 cnt = 0; 87 ll n, m = 0, fa, k = 0, maxx = 0, ans = 0; 88 scanf("%lld", &n); 89 for (ll i = 0; i <= n; i++) 90 sum[i] = out[i] = sizx[i] = dep[i] = 0, head[i] = -1; 91 for (ll i = 2; i <= n; i++) 92 { 93 scanf("%lld", &fa), out[fa]++; 94 add(fa, i), add(i, fa); 95 } 96 dfs1(1, 0); 97 dfs2(1, 0); 98 for (ll i = 1; i <= n; i++) 99 { 100 k += sizx[i]; 101 if (!out[i]) 102 vec.push_back(i); 103 } 104 m = vec.size(); 105 for (ll i = 0; i < m; i++) 106 { 107 ll res = (dep[vec[i]]) * (n - 1) - sum[vec[i]] + dep[vec[i]]; 108 ans = max(ans, res + k); 109 } 110 printf("%lld ", ans); 111 } 112 }
