//题意:
//给你n个学校,其中每一个学校都和一些其他学校有交流,但是这些边都是单向的。你至少需要给几个学校
//传递消息可以使全部学校都收到消息,第二问你最少添加几条边可以使它变成一个强连通图
//题解:
//首先是第一问,这个你只需要找出来一共有几个连通块就可以了,也相当于有几个入度为0的点(这个时候就不是
//之前的图,是要缩点后的图来找出入度)
//第二问:找出来所有点中max(入度为0,出度为0)
为什么要找它们的最大值:(黑边为原来存在的,红边是添加的,使这个图变成强连通图的)

或者
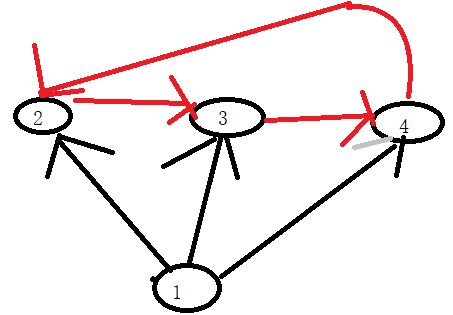
反正不管怎么连边,它们对少需要3条边才可以成为强连通图(从任意一个点可以到达图中的其他点)
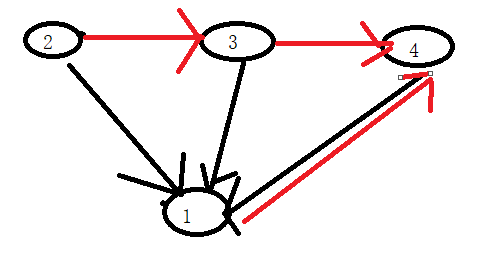
或者
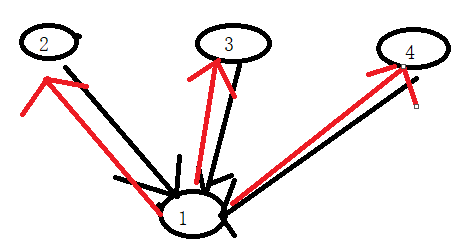
上代码:

1 //题意: 2 //给你n个学校,其中每一个学校都和一些其他学校有交流,但是这些边都是单向的。你至少需要给几个学校 3 //传递消息可以使全部学校都收到消息,第二问你最少添加几条边可以使它变成一个强连通图 4 //题解: 5 //首先是第一问,这个你只需要找出来一共有几个连通块就可以了,也相当于有几个入度为0的点(这个时候就不是 6 //之前的图,是要缩点后的图来找出入度) 7 //第二问:找出来所有点中max(入度为0,出度为0) 8 #include<stdio.h> 9 #include<string.h> 10 #include<iostream> 11 #include<algorithm> 12 #include<map> 13 #include<math.h> 14 #include<set> 15 #include<queue> 16 using namespace std; 17 typedef long long ll; 18 const int maxn=105; 19 const int mod=26; 20 const int INF=0x3f3f3f3f; 21 const int block=300; 22 struct edge 23 { 24 int u,v,next; 25 bool sign; 26 }e[maxn*maxn]; 27 int head[maxn],cnt; 28 void add_edge(int x,int y) 29 { 30 e[cnt].u=x; 31 e[cnt].v=y; 32 e[cnt].next=head[x]; 33 head[x]=cnt++; 34 } 35 int dfn[maxn],low[maxn],stacks[maxn],top,tot; 36 int taj; 37 int belong[maxn],visit[maxn]; 38 vector<int>w[maxn]; 39 void tarjan(int x,int fx) 40 { 41 dfn[x]=low[x]=++tot; 42 stacks[top++]=x; 43 visit[x]=1; 44 for(int i=head[x];i!=-1;i=e[i].next) 45 { 46 int v=e[i].v; 47 if(!dfn[v]) 48 { 49 tarjan(v,x); 50 low[x]=min(low[x],low[v]); 51 if(dfn[x]<low[v]) 52 { 53 e[i].sign=1; 54 } 55 } 56 else if(visit[v]) 57 { 58 low[x]=min(low[x],dfn[v]); 59 } 60 } 61 if(low[x]==dfn[x]) 62 { 63 int now; 64 taj++; 65 w[taj].clear(); 66 do{ 67 now=stacks[--top]; 68 visit[now]=0; 69 belong[now]=taj; 70 w[taj].push_back(now); 71 }while(now!=x); 72 } 73 } 74 void tarjan_init(int n) 75 { 76 memset(visit,0,sizeof(visit)); 77 top=tot=taj=0; 78 for(int i=1;i<=n;++i) 79 { 80 if(!dfn[i]) tarjan(i,i); 81 } 82 } 83 vector<int>g[maxn]; 84 int cu[maxn],ru[maxn]; 85 void suodian() 86 { 87 memset(cu,0,sizeof(cu)); 88 memset(ru,0,sizeof(ru)); 89 for(int i=1;i<=taj;++i) 90 g[i].clear(); 91 for(int i=0;i<cnt;++i) 92 { 93 int u=belong[e[i].u]; 94 int v=belong[e[i].v]; 95 if(u!=v) g[u].push_back(v),cu[u]++,ru[v]++;//printf("%d %d ",u,v); 96 } 97 } 98 int vis[maxn]; 99 void init() 100 { 101 memset(head,-1,sizeof(head)); 102 cnt=0; 103 } 104 int main() 105 { 106 int a,n; 107 scanf("%d",&n); 108 init(); 109 for(int i=1;i<=n;++i) 110 { 111 while(~scanf("%d",&a) && a) 112 { 113 add_edge(i,a); 114 } 115 } 116 tarjan_init(n); 117 if(taj==1) 118 { 119 printf("1 0 "); 120 return 0; 121 } 122 // for(int i=1;i<=n;i++) 123 // 124 // if(dfn[i]==-1) 125 // 126 // tarjan(i,-1); 127 //for(int i) 128 //printf("%d** ",taj); 129 suodian(); 130 int ans1=0,ans2=0; 131 for(int i=1;i<=taj;++i) 132 { 133 if(ru[i]==0) 134 ans1++; 135 if(cu[i]==0) 136 ans2++; 137 } 138 printf("%d %d ",ans1,max(ans1,ans2)); 139 return 0; 140 }
