一、概述:
Kruskal算法也是一种求得最小生成树的算法,与Prim算法不同的是,它的时间复杂度为O(eloge)(e为网中的边数),所以,适合于求边稀疏的网的最小生成树(有关最小生成树的概念和Prim算法见最小生成树-Prim算法)。
二、原理:
Kruskal算法是一种贪心的思想,其原理是,设最小生成树的集合为S,先将无向图中的每一条边由小到大排序,然后从小到大依次将边加入S中,每次加入时需要先判断将此边加入生成树中是否成环,重复上述过程,直至生成树中包含所有的点。判断是否成环需要用到并查集这种数据结构。
图示:
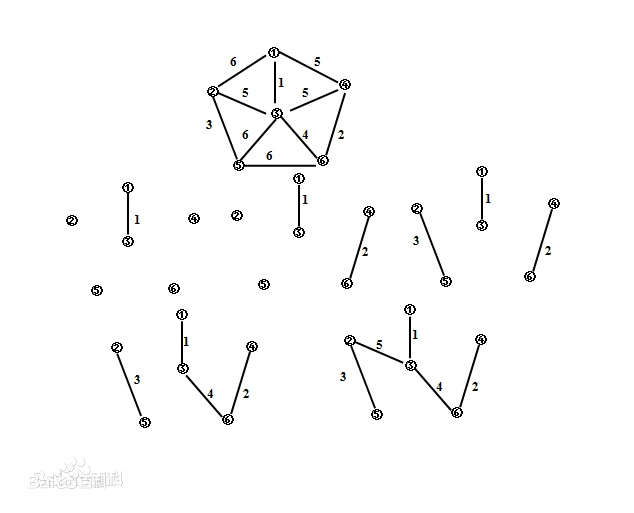
三、示例代码(畅通工程)
Description
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 );随后的N(N-1)/2行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从1到N编号。
当N为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最小的公路总长度。
Sample Input
3
1 2 1
1 3 2
2 3 4
4
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
0
Sample Output
3
5
#include <bits/stdc++.h>
using namespace std;
int n;
int pre[105]; // 记录根节点
struct edge{
int v1; // 顶点
int v2; // 顶点
int weight; // 权值
};
// 并查集-查
int Search(int root) {
if(root != pre[root]) {
root = Search(pre[root]);
}
return pre[root];
}
// 并查集-并
void Merge(int root1, int root2) {
int a, b;
a = Search(root1), b = Search(root2);
if(a != b) {
pre[a] = b;
}
}
bool cmp(edge x, edge y) {
return x.weight < y.weight;
}
int Kruskal(edge Edge[]) {
// ans记录权值之和,cnt记录当前生成树中边的个数
int ans = 0, cnt = 0, u, v;
// 将边集合排序
sort(Edge+1, Edge+n * (n - 1) / 2+1, cmp);
for (int i = 1; i <= n * (n - 1) / 2; ++i) {
// 已找出最小生成树,退出循环
if(cnt >= n-1) break;
// 取最小权值的边
u = Edge[i].v1;
v = Edge[i].v2;
// 不成环则加入最小生成树
if(Search(u) != Search(v)) {
ans += Edge[i].weight;
cnt++;
Merge(u, v);
}
}
return ans;
}
int main() {
int a, b;
while(~scanf("%d", &n)) {
if (!n) break;
int ans = 0, cost;
edge Edge[n*(n-1)/2+5];
// 数组初始化
for (int i = 1; i <= n; ++i) {
pre[i] = i;
}
for (int i = 1; i <= n * (n - 1) / 2; i++) {
cin >> a >> b >> cost;
Edge[i].v1 = a;
Edge[i].v2 = b;
Edge[i].weight = cost;
}
ans = Kruskal(Edge);
cout << ans << endl;
}
return 0;
}