已知函数(f(x)=mx^3+nx^2(n,min R,m>n,m eq 0))的图像在((2,f(2)))处切线与(x)轴平行
((1)) 判断(n,m)正负
((2)) 若函数(f(x))在区间([n,m])上有(m-n^2),求(m)的值
解答:
((1))
[f'(x)=3mx^2+2nx
]
[f'(2)=0
]
[12m+4n=0
]
[-3m=n
]
[m>0,n<0
]
((2))
[f'(x)=3mx^2-6mx
]
[f'(x)=3mx(x-2)
]
可以推出(f'(x))的大致函数图像
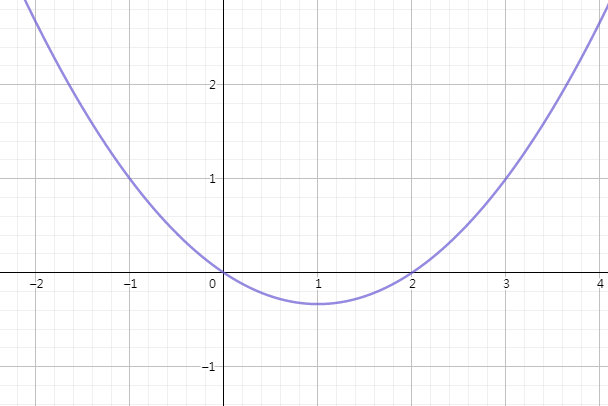
再结合(f(x))的零点((0,0),(3,0))画出(f(x))大致图像
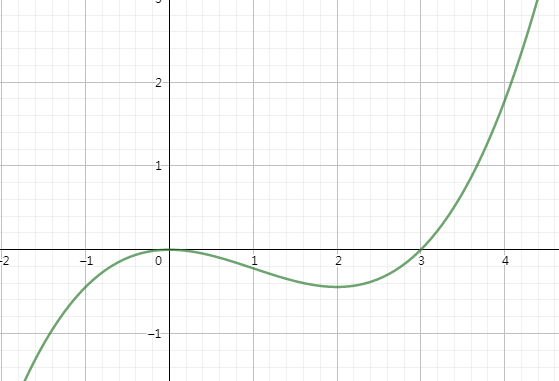
当(mle 3)时
[f_{max}(x)=f(0)=0
]
[m-n^2=0,-3m=n
]
解出
[m=frac{1}{9}
]
当(m>3)时
[f_{max}(x)=f(m)=m^4-3m^3
]
[m^4-3m^3=m-n^2
]
[m^4-3m^3+9m^2-m=0
]
[g(m)=m^3-3m^2+9m-1
]
[g'(m)=3m^2-6m+9
]
[g'(m)=3(m-1)^2+6
]
所以(g(m))在定义域上单调增
又因为(g(3)>0),所以(m<3),不成立
所以(m=frac{1}{9})