定义
(prufer)是无根树的一种数列,在组合数学中,(prufer)数列由有一个对于顶点标过号的树转化来的数列,点数为(n)的树转化来的(prufer)数列长度为(n-2)
每个(prufer)数列唯一对应一种形态的无根树
无根树构造(prufer)序列
重复以下步骤 直到树中只剩下两个点:
(1.)找到编号最小的度数为(1)的点
(2.)删除该点并在序列尾部添加与该节点相连的节点编号
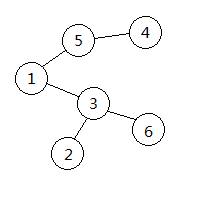
以该图为例
先将点(2)删除 然后序列中加入(3) 得到({3})
将点(4)删除,序列中加入(5) 得到({3,5})
然后依次删除(5、1),得到({3,5,1,3})
(prufer)序列构造无根树
初始化点集是全集({1,2,3,4,5,6})
(1.)每次取出(prufer)序列中最前面的元素(u)
(2.)在点集中找到最小的没有在(prufer)序列中出现过的元素(v)
(3.) 在(u,v)之间连边,然后在序列中删除(u),在点集中删除(v)
(4.)清空(prufer)序列之后,点集中的最后两个元素连边
性质
(1.)一颗(n)个节点的无根树唯一地对应一个长度为(n-2)的(prufer)序列,数列中每个数都在(1-n)范围内
(2.) (prufer)序列中某个编号出现次数为该编号节点度数(-1)(去掉父亲边)
(3.) (n)个点的无向完全图的生成树计数(n^{n-2}),即(n)个点的有标号无根树计数
(4.) (n)个节点的度依次为(d_1,d_2,d_3……d_n)的无根树共有(frac{(n-2)!}{prodlimits_{i=1}^{n}(d_i-1)!})
其实就是可重元素全排列公式