根据我做的一些水题总结的
网络流真的神奇,似乎有生命,可以自动将全图调整到最优状态
二分图最大匹配
网络流求解二分图最大匹配应该很普及了吧,只要左部每个节点连一个源点,右部每个结点连一个汇点,然后左部向右部连边就连一条流量为(1)的边,跑最大流
例题:
展开查看
```cpp
#include
using namespace std;
inline int read()
{
int x=0,f=1;
char ch;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') f=0,ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?x:-x;
}
const int inf=0x7f7f7f7f;
int n,m,st,ed,ret;
int head[1010],cur[1010],d[1010],cnt=1;
struct point
{
int nxt,to,val;
}a[200010];
inline void add(int x,int y,int z)
{
a[++cnt].nxt=head[x];
a[cnt].to=y;
a[cnt].val=z;
head[x]=cnt;
}
queue q;
inline bool bfs()
{
for(int i=1;i<=n+m+2;++i)
{
cur[i]=head[i];
d[i]=0;
}
q.push(st);d[st]=1;
while(!q.empty())
{
int now=q.front();
q.pop();
for(int i=head[now];i;i=a[i].nxt)
{
int t=a[i].to;
if(!d[t]&&a[i].val)
{
d[t]=d[now]+1;
q.push(t);
}
}
}
return d[ed];
}
inline int dfs(int now,int c)
{
if(now==ed||!c) return c;
int ret=c,f;
for(int i=cur[now];i;i=a[i].nxt)
{
cur[now]=i;
int t=a[i].to;
if(d[t]==d[now]+1)
{
f=dfs(t,min(ret,a[i].val));
a[i].val-=f;
a[i^1].val+=f;
ret-=f;
if(!ret) return c;
}
}
if(ret==c) d[now]=0;
return c-ret;
}
inline void dinic()
{
while(bfs()) ret+=dfs(st,inf);
if(!ret) puts("No Solution!");
else
{
printf("%d
",ret);
for(int now=1;now<=m;++now)//m<=n
{
for(int i=head[now];i;i=a[i].nxt)
{
int t=a[i].to;
if(t==st||t==ed||a[i].val) continue;
printf("%d %d
",now,t);//求方案,暴力判断每条边流量是否为0;
break;
}
}
}
}
signed main()//二分图网络流模型
{
m=read(),n=read();
st=n+m+1,ed=n+m+2;
for(int i=1;i<=m;++i) add(st,i,1),add(i,st,0);
for(int i=m+1;i<=n+m;++i) add(i,ed,1),add(ed,i,0);
for(int x,y;;)
{
x=read(),y=read();
if(!~x&&!~y) break;
add(x,y,1);
add(y,x,0);
}
dinic();
return 0;
}
```
最大闭合权子图
有一个(DAG),每个点带有权值
我们规定选择一个点后,这个点能够达到的节点必须全部选择,求如何选择使得节点的权值之和最大?
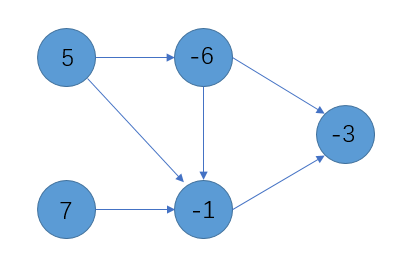
如图,选择权值为(5)的节点后必须选择权值为(-1,-6,-3)的节点,选择权值为(7)的节点后必须选择权值为(-1,-3)的节点
对于这一类问题,我们通常将所有正权点与超级源点相连,所有负权点与超级汇点相连,边权取反
然后将原来的边权全部设置为无穷
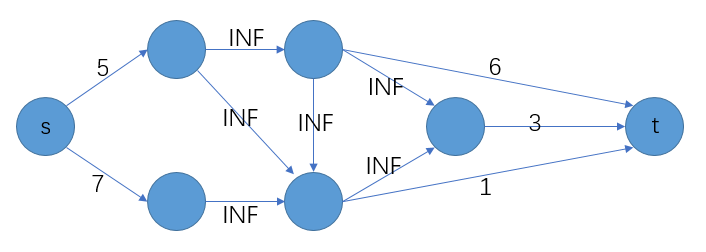
答案即为原图中所有正点权和减去这张图中的最小割
证明:首先我们必定不会割中间的无穷边,所以这张图中的最小割一定是简单割
简单割:所有割边都直接与(S)或(T)相连
那么我们考虑与(S)相连的被割掉的边,意味这只有这些边能联通的与(T)相连的边不用被割掉
在原图中也就意味着我们舍弃掉这些正权点,那么只有这些正权点能够到达的负权点的权值不必再减去
与(S)相连的边没有被割掉,说明我们要割掉这些点能到达的与(T)相连的边
在原图中意味中我们选择了这些正权点,那么这些正权点能够到达的负权点的权值需要减去
如在上面的图中,我们割去与(S)相连的,容量为(5)的边,那么显然与(T)相连,容量为(6)的边不用再割去,也就是说我们不选权值为(5)的点,权值为(-6)的点也不必再选
所以最后(ans=)所有正点权之和(-)新图最小割
例题:
展开查看
```cpp
#include
using namespace std;
inline int read()
{
int x=0,f=1;
char ch;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') f=0,ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?x:-x;
}
const int inf=0x7f7f7f7f;
char ch;
int n,m,st,ed,ret,sum;
int head[1010],cur[1010],d[1010],cnt=1;
struct point
{
int nxt,to,val;
}a[200010];
inline void add(int x,int y,int z)
{
a[++cnt].nxt=head[x];
a[cnt].to=y;
a[cnt].val=z;
head[x]=cnt;
}
queue q;
inline bool bfs()
{
for(int i=1;i<=n+m+2;++i)
{
cur[i]=head[i];
d[i]=0;
}
q.push(st);d[st]=1;
while(!q.empty())
{
int now=q.front();
q.pop();
for(int i=head[now];i;i=a[i].nxt)
{
int t=a[i].to;
if(!d[t]&&a[i].val)
{
d[t]=d[now]+1;
q.push(t);
}
}
}
return d[ed];
}
inline int dfs(int now,int c)
{
if(now==ed||!c) return c;
int ret=c,f;
for(int i=cur[now];i;i=a[i].nxt)
{
cur[now]=i;
int t=a[i].to;
if(d[t]==d[now]+1)
{
f=dfs(t,min(ret,a[i].val));
a[i].val-=f;
a[i^1].val+=f;
ret-=f;
if(!ret) return c;
}
}
if(ret==c) d[now]=0;
return c-ret;
}
inline int dinic()
{
while(bfs()) ret+=dfs(st,inf);
return ret;
}
signed main()//最大权闭合子图->最小割模型
{
m=read(),n=read();
st=n+m+1,ed=n+m+2;
for(int x,i=1;i<=m;++i)
{
x=read();
sum+=x;
add(st,i,x);
add(i,st,0);
while("tyx")
{
scanf("%d%c",&x,&ch);
add(i,x+m,inf);
add(x+m,i,0);
if(ch=='
'||ch=='
') break;
}
}
for(int x,i=1;i<=n;++i)
{
x=read();
add(m+i,ed,x);
add(ed,m+i,0);
}
sum-=dinic();
for(int i=1;i<=m;++i) if(d[i]) printf("%d ",i);
putchar('
');
for(int i=1;i<=n;++i) if(d[i+m]) printf("%d ",i);
putchar('
');
printf("%d
",sum);
return 0;
}
```
DAG最小路径覆盖
其实拆完点都是二分图,然后就最小路径覆盖条数=节点数-最大匹配就好了,没什么可说了
例题有个挺不错的,不多解释了
展开查看
```cpp
#include
using namespace std;
inline int read()
{
int x=0;
char ch,f=1;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') f=0,ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?x:-x;
}
const int inf=0x7f7f7f7f;
int n,tyx,num;
int st=10001,ed=10002;
int nxt[10010];
int nz[10010];
int head[10010],cur[10010],d[10010],cnt=1;
struct point
{
int nxt,to,val;
}a[200010];
inline void add(int x,int y,int z)
{
a[++cnt].nxt=head[x];
a[cnt].to=y;
a[cnt].val=z;
head[x]=cnt;
}
inline bool check(int x,int y)
{
int t=ceil(sqrt(x+y));
return t*t==(x+y);
}
queue q;
inline bool bfs()
{
for(int i=1;i<=num;++i)
{
cur[i]=head[i];
cur[i+5000]=head[i+5000];
d[i]=d[i+5000]=0;
}
for(int i=10001;i<=10002;++i)
{
cur[i]=head[i];
d[i]=0;
}
q.push(st);d[st]=1;
while(!q.empty())
{
int now=q.front();
q.pop();
for(int i=head[now];i;i=a[i].nxt)
{
int t=a[i].to;
if(!d[t]&&a[i].val)
{
d[t]=d[now]+1;
q.push(t);
}
}
}
return d[ed];
}
inline int dfs(int now,int c)
{
if(now==ed||!c) return c;
int ret=c,f;
for(int i=cur[now];i;i=a[i].nxt)
{
cur[now]=i;
int t=a[i].to;
if(d[t]==d[now]+1)
{
f=dfs(t,min(ret,a[i].val));
if(!f) continue;
a[i].val-=f;
a[i^1].val+=f;
ret-=f;
if(t!=ed) nxt[now]=(t<=5000?t:t-5000);
if(!ret) return c;
}
}
if(ret==c) d[now]=0;
return c-ret;
}
inline int dinic()
{
int ret=0;
while(bfs()) ret+=dfs(st,inf);
return ret;
}
signed main()//转化为最小路径覆盖,当总点数-最大匹配>柱子数量时退出
{
n=read();
while(tyx<=n)
{
++num;
add(st,num,1);
add(num,st,0);
add(num+5000,ed,1);
add(ed,num+5000,0);
for(int i=1;i 二分图多重匹配
这个本来应该放在二分图全家桶里吧……不过既然会网络流做法懒得管那个了
扔到题目里面讲吧,看明白一道题其他的都差不多
构造最小割
一些题目大意类似:某些物品有一些收益,但是选择了某种物品就不能选择另外一些物品,求最大收益
对于这一类问题,我们可以通过构造最小割实现,基本思路是先求出没有限制的总收益,再通过求出最小割减去需要减去的最少收益
例题:
洛谷P2774 方格取数问题
洛谷P4313 文理分科
洛谷P1935 [国家集训队]圈地计划
构造最大流跑费用流
一些题目要求达到某些要求的同时要求最小代价,可以用过构造多种满足最大流的条件来跑费用流实现
洛谷P1251 餐巾计划问题
洛谷P3358 最长k可重区间集问题
二分图最优匹配
左部节点向(S)连边,右部节点向(T)连边,容量为(1),费用为(0)。
左部向右部连边,容量为(1),费用为给定费用
然后跑最大费用最大流
啊啊啊费用流这么好写我为什么我要去(KM)啊!
对偶图
神仙结论:平面图最小割等于对偶图最短路
懒得解释了……直接扔个题目扔个代码得了
今天好颓啊
展开查看
```cpp
#include
using namespace std;
inline int read()
{
int x=0,f=1;
char ch;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') f=0,ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?x:-x;
}
int n,m,st,ed,tot;
int val[1010][1010][4];
int id[1010][1010][2];
int head[8000010],cnt;
struct point
{
int nxt,to,val;
}a[16000010];
inline void add(int x,int y,int z)
{
a[++cnt]=(point){head[x],y,z};head[x]=cnt;
a[++cnt]=(point){head[y],x,z};head[y]=cnt;
}
typedef pair p;
priority_queue,greater > q;
int dis[8000010];
bool vis[8000010];
inline void spfa()
{
memset(dis,0x3f,sizeof(dis));
dis[st]=0;
q.push(p(0,st));
while(!q.empty())
{
int now=q.top().second;
q.pop();
if(vis[now]) continue;
vis[now]=1;
for(int i=head[now];i;i=a[i].nxt)
{
int t=a[i].to;
if(dis[t]>dis[now]+a[i].val)
{
dis[t]=dis[now]+a[i].val;
q.push(p(dis[t],t));
}
}
}
}
inline void solve1()//n==1
{
int ret=0x3f3f3f3f;
for(int i=1;ifor(int i=1;i<n;++i) add(st,id[i][1][0],val[i][1][2]);//下半部连st
for(int j=1;j<m;++j) add(st,id[n-1][j][0],val[n][j][1]);
for(int j=1;j<m;++j) add(id[1][j][1],ed,val[1][j][1]);//上半部连ed
for(int i=1;i<n;++i) add(id[i][m-1][1],ed,val[i][m][2]);
spfa();
printf("%d
",dis[ed]);
return 0;
}
</code></pre>
</details>