先让大家来看一幅图,这幅图是V8引擎4.7版本和4.9版本Math.Random()函数的值的分布图,我可以这么理解 。从下图中,也许你会认为这是个二维码?其实这幅图告诉我们一个道理,第二张图的点的分布更加的密集,也就是说Math.Random()函数能表示的数字更多了,大家在.NET中肯定也用过GUID吧,至于GUID为什么会永不重复,大家有没有想过呢?

还是让我们先来看看官方怎么解释Math.Random()吧,它是返回了一个正数,这个正数介于0~1之间,以伪随机的方式在这个范围内波动。Math.Random()函数在JS中也被大量的使用到。它的核心原理是用到了(伪随机数生成器PRNG),随机数从一个内部状态派生而来,通过一个固定的算法来得到每次不同的随机数。所以对于一个已知的内部初始状态,随机数的队列是可以计算出来的;自从位大小N被限制以来,PRNG生成器会重复它自己之前的工作。置换图的周期上界最大范围为2n 。
下面带大家看看PRNG(伪随机数)生成算法。伪随机数,为什么说不是 真正的随机数呢?因为随机数是永不重复的!伪随机数只是“一群隔得很近的数”,用我们数学当中的讲法就是,趋近于某个数,但是不等于某个数,也就是它的“极限”等于某个数,大学数学里面有说到。下面是数学解释:
 - 概率分布在
- 概率分布在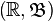 上 (当
上 (当 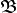 在柏来尔域上)。
在柏来尔域上)。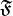 - 非空柏来尔域
- 非空柏来尔域  ,比如
,比如 ![mathfrak{F}=left{left(-infty,t
ight] : tinmathbb{R}
ight}](https://upload.wikimedia.org/math/9/b/d/9bdb018ba77d4114b80272cc1f828b70.png) ,左边的式子意思是,t<=0,t是实数;如果
,左边的式子意思是,t<=0,t是实数;如果 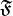 没有定义,那就可能是
没有定义,那就可能是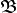 或者
或者![left{left(-infty,t
ight] : tinmathbb{R}
ight}](https://upload.wikimedia.org/math/5/3/c/53c5c8649f403e4120e9dbc8f6308e6c.png) 被附加在上下文当中。
被附加在上下文当中。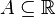 非空集合(不一定在柏来尔域中),
非空集合(不一定在柏来尔域中), 是一个集合,它是介于
是一个集合,它是介于  和它内部本身之间的。假设P是均匀分布在(0,]之间,那么A也有可能是在(0,1]之间的,如果A没有被定义,那么它就会假定包含在P的支持里并包含在它的内部,且依赖于上下文环境。
和它内部本身之间的。假设P是均匀分布在(0,]之间,那么A也有可能是在(0,1]之间的,如果A没有被定义,那么它就会假定包含在P的支持里并包含在它的内部,且依赖于上下文环境。- 我们称一个函数:
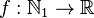 (当
(当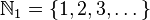 为正数集合,对于
为正数集合,对于  来说伪随机数生成器,对于给定的
来说伪随机数生成器,对于给定的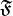 来说当且仅当在A中)
来说当且仅当在A中)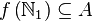
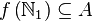
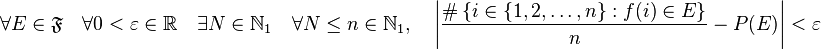
以上的介绍是不是晕掉了呢?没关系,上面的只是让你对Random算法有个大概的了解,并不要求你完全理解(其实我也不太理解)。其实事实上,关于PRNG算法有很多的实现方式,最有名的就当 Mersenne-Twister和LCG了。每种不同的算法都有它自己的特点,有点甚至是缺点。想当然的说:其实只需要用很少的时间,就可以完成整个流程的计算,以及长周期计算。当性能,内存使用情况,计算周期都能被很容易的被估计到和计算到时,Random分布的质量将会更难被决定,测试的难度也会更大。
下面的代码就是把2个16位的state(状态码)融合在一起。32位的数字转换成浮点型,并以介于0~1的形式呈现给我们。
uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
state0 = 18030 * (state0 & 0xffff) + (state0 >> 16);
state1 = 30903 * (state1 & 0xffff) + (state1 >> 16);
return state0 << 16 + (state1 & 0xffff);
MWC1616 算法用到了少量的内存,以及快速的运行速度,但是它的品质(quality)却是不敢让人恭维的,它的特性有如下几点:
- 数字的范围能从232提升到252次方并让它只介于0~1之间。
- 更重要的state1依赖于state0的值(见上面的代码)。
- 数字的最大跨度可以达到 232 但是如果选择了一个不好的初始状态,周期长度会缩短到4千万以下。
因为64位的会出很多问题(GOOGLE研究员说的),GOOGLE采用了一种新的xorshift128+算法,看名字大家也知道了,是128位的,周期是 2128 - 1.
uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
uint64_t s1 = state0;
uint64_t s0 = state1;
state0 = s0;
s1 ^= s1 << 23;
s1 ^= s1 >> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
state1 = s1;
return state0 + state1;
}
其实通过这篇文章,大家只能对这个函数有个大概的了解,但是我可以让大家明白一点,看过这篇文章后,您还会怀念IE6吗?O(∩_∩)O哈哈~