题目链接:
题目分析:
裸的三分套三分啊,三分为什么是单峰的可以去看这篇博客的证明,感觉是目前写得最清楚的一篇
不过其实最开始没有很搞懂三分求单峰函数最值是个啥东西,所以这里还是记录一下
手画图,不要吐槽有多丑
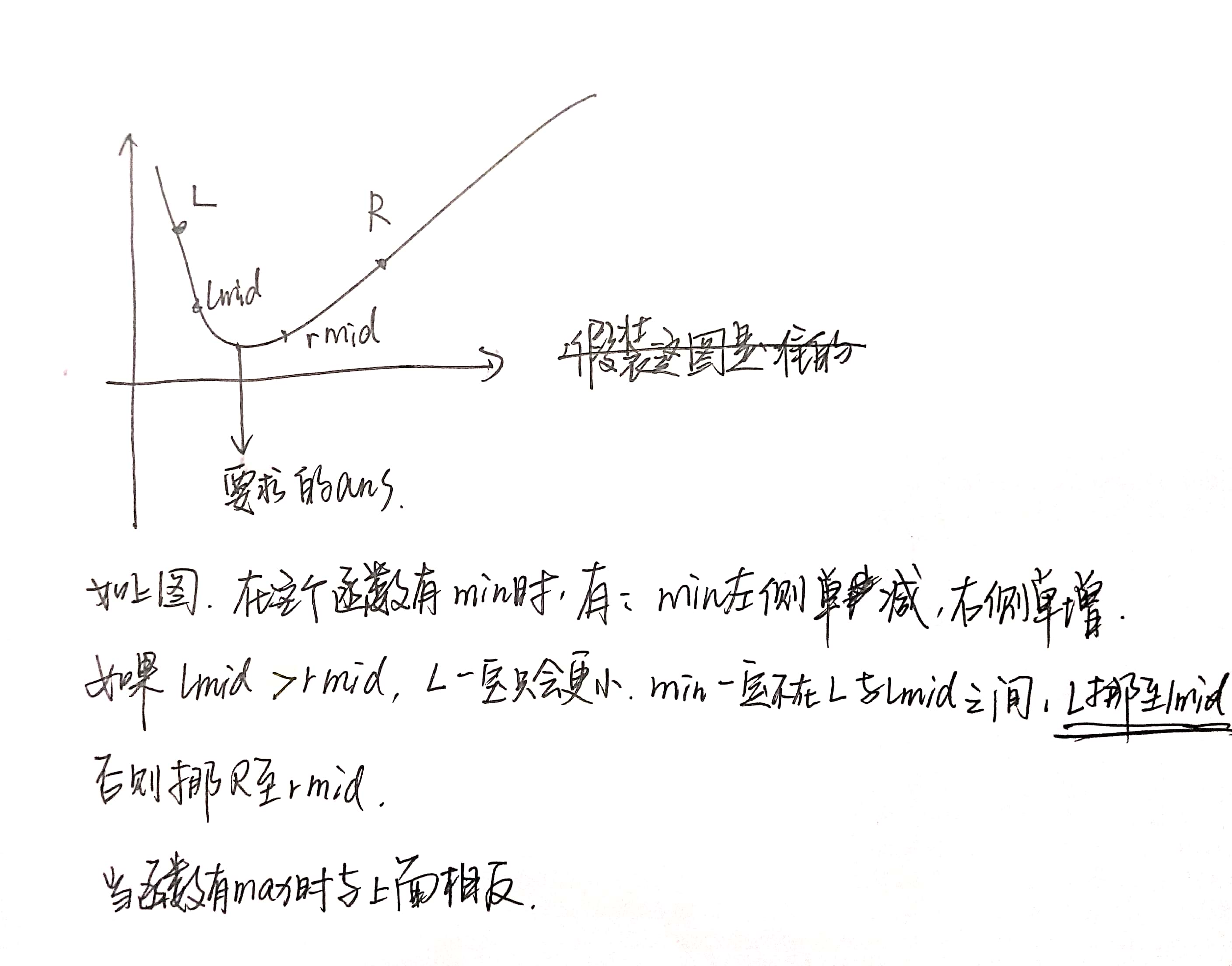
代码:
#include <bits/stdc++.h>
#define N (2000 + 10)
using namespace std;
inline int read() {
int cnt = 0, f = 1; char c = getchar();
while (!isdigit(c)) {if (c == '-') f = -f; c = getchar();}
while (isdigit(c)) {cnt = (cnt << 3) + (cnt << 1) + c - '0'; c = getchar();}
return cnt * f;
}
int x, y;
int P, Q, R;
const double eps = 1e-8;
int dcmp(double x) {
if (fabs(x) < eps) return 0;
else return x < 0 ? -1 : 1;
}
struct Vector{
double x; double y;
Vector (){};
Vector (double x_, double y_) : x (x_), y (y_) { };
}A, B, C, D;
typedef Vector Point;
struct Line{
Point u; Point v;
Line (Point u_, Point v_) : u (u_), v(v_) { };
};
typedef Line Segment;
Vector operator + (Vector A, Vector B) {
return Vector (A.x + B.x, A.y + B.y);
}
Vector operator - (Vector A, Vector B) {
return Vector (A.x - B.x, A.y - B.y);
}
Vector operator / (Vector A, double p) {
return Vector (A.x / p, A.y / p);
}
double Dot (Vector a, Vector b) {
return a.x * b.x + a.y * b.y;
}
double Length(Vector A){
return sqrt(Dot(A, A));
}
double calc(Point X) {
Point l = C, r = D;
while (Length(l - r) > eps) {
Point x = (r - l) / 3;
Point lmid = l + x, rmid = r - x;
double ans1 = Length(lmid - D) / Q + Length(X - lmid) / R;
double ans2 = Length(rmid - D) / Q + Length(X - rmid) / R;
if (ans2 - ans1 > eps) r = rmid;
else l = lmid;
}
return Length(l - D) / Q + Length(X - l) / R;
}
double solve() {
Point l = A, r = B;
while (Length(l - r) > eps) {
Point x = (r - l) / 3;
Point lmid = l + x, rmid = r - x;
double ans1 = calc(lmid) + Length(lmid - A) / P;
double ans2 = calc(rmid) + Length(rmid - A) / P;
if (ans2 - ans1 > eps) r = rmid;
else l = lmid;
} return calc(l) + Length(l - A) / P;
}
int main() {
x = read(), y = read();
A = Point(x, y);
x = read(), y = read();
B = Point(x, y);
x = read(), y = read();
C = Point(x, y);
x = read(), y = read();
D = Point(x, y);
P = read(), Q = read(), R = read();
return printf("%0.2lf", solve()), 0;
}