On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.
One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.
To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.
Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!
The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).
If there is an error and it is actually not possible to beat the level, output a single integer -1.
Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.
The next k lines should each contain one of the following, describing the moves in the order they must be done:
- row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
- col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".
If there are multiple optimal solutions, output any one of them.
3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1
4
row 1
row 1
col 4
row 3
3 3
0 0 0
0 1 0
0 0 0
-1
3 3
1 1 1
1 1 1
1 1 1
3
row 1
row 2
row 3
In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:
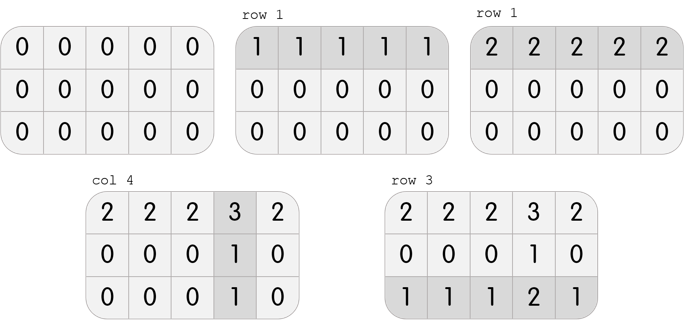
In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.
In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:
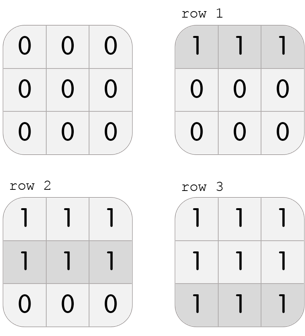
Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.
题意:
给定n行m列数字,每次可以让一行或一列都减一,求出让全部数字全为0的最小的次数,没有则输出-1;
思路:
就是对行和列处理,注意下n和m的大小就行。
第一次比赛打了三道。。。上了一波大分。
#include <bits/stdc++.h> using namespace std; const int N = 200; int n, m, a[N][N], c[N], r[N], ans; int check() { for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) if (a[i][j]) return 0; return 1; } void row_man() { for (int i = 0; i < n; i++) { int mi = a[i][0]; for (int j = 1; j < m; j++) mi = min(mi, a[i][j]); r[i] = mi; ans += r[i]; for (int j = 0; j < m; j++) a[i][j] -= mi; } } void col_man() { for (int j = 0; j < m; j++) { int mi = a[0][j]; for (int i = 1; i < n; i++) mi = min(mi, a[i][j]); c[j] = mi; ans += c[j]; for (int i = 0; i < n; i++) a[i][j] -= mi; } } int main() { cin >> n >> m; for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) scanf("%d", &a[i][j]); if (n > m) { col_man(); row_man(); } else { row_man(); col_man(); } if (!check()) puts("-1"); else { cout << ans << endl; for (int i = 0; i < n; i++) for (int j = 0; j < r[i]; j++) printf("row %d ", i + 1); for (int i = 0; i < m; i++) for (int j = 0; j < c[i]; j++) printf("col %d ", i + 1); } }