空间直线同空间中三维椭球相交,其交点即为空间直线方程同椭球方程的解,对于空间直线方程,只要知道两点空间坐标即可,而欧拉角不为零的三维椭球方程则较难描述,但可以考虑对椭球进行变换,使其欧拉角为零,进而转化为标准椭球,标准椭球方程则容易描述,相应在对椭球进行变换的同时也许对空间直线进行相应的变换。由此,通过标准椭球方程同变换后的直线方程进行联立求解,即可获取交点坐标,下面简述求解过程及列出主要的计算公式。
约定本文采用右手系,空间旋转顺序为Z-Y-X。


6、示例
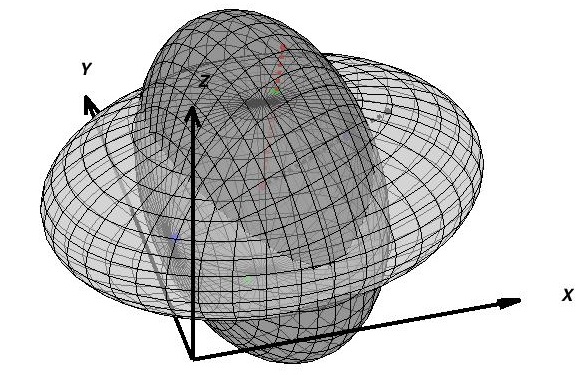
空间直线同空间中三维椭球相交,其交点即为空间直线方程同椭球方程的解,对于空间直线方程,只要知道两点空间坐标即可,而欧拉角不为零的三维椭球方程则较难描述,但可以考虑对椭球进行变换,使其欧拉角为零,进而转化为标准椭球,标准椭球方程则容易描述,相应在对椭球进行变换的同时也许对空间直线进行相应的变换。由此,通过标准椭球方程同变换后的直线方程进行联立求解,即可获取交点坐标,下面简述求解过程及列出主要的计算公式。
约定本文采用右手系,空间旋转顺序为Z-Y-X。


6、示例
