1、旋转的四元数表示
空间中的旋转可用一个四元数来表述,如点 $P(\,x,y,z\,)$ 绕向量 $V(\,u,v,w\,)$ 旋转 ,此旋转过程可表示为四元数 Q $[\,\,cos( frac{ heta}{2} ),\,sin( frac{ heta}{2} )cdot (u,v,w)\,]$ 。
2、基本旋转的四元数表示
空间中的三维旋转可视为绕三个基本轴的旋转组合叠加,绕 $x,y,z$ 三个基本轴旋转角度分别为 $ phi, heta,psi$ ,则三个基本旋转的四元素可表征为:

3、复合旋转的四元数表示
绕三个基本轴的旋转次序不同,其表征的空间旋转也不同,下面给出顺序为 $ZYX$ 、$XYZ$ 时的结果及相应推导过程。
3.1 对于 $ZYX$ ,其表征的旋转过程定义为:

且已知四元数,可以反求欧拉角
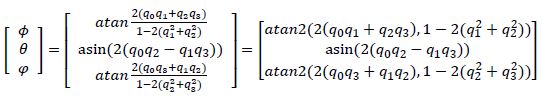
3.2 对于 $XYZ$ ,其表征的旋转过程定义为:

4、空间点旋转表示

5、空间点旋转的逆过程
对于坐标系中点 $P(\,x,y,z\,)$ ,其旋转欧拉角为 $ (\,phi, heta,psi\,)$ ,按照 $ZYX$ 顺序旋转后坐标点为 $P'(\,x',y',z'\,)$ ,完成 P 到 P’ 转换过程,其逆过程,即 P’ 到 P 的变换则按照欧拉角 $ (\,-phi,- heta,-psi\,)$,的顺序进行。
6、程序实现
按照如上表述,编写测试算例,展示一个椭圆颗粒的的空间变换旋转过程。
1 clc;clear; 2 close all; 3 4 % 采用四元数方法定义旋转 5 % 采用右手系,旋转次序按照 Z-Y-X 进行 6 7 %% 原始椭圆形状定义 8 psi = 0:pi/20:pi; 9 sita = 0:pi/20:2*pi; 10 a = 8; 11 b = 3.5; 12 c = 2; 13 x0 = 0; 14 y0 = 0; 15 z0 = 0; 16 17 x = zeros( length(psi), length(sita) ); 18 y = zeros( length(psi), length(sita) ); 19 z = zeros( length(psi), length(sita) ); 20 for j = 1 : length( psi ) 21 for i = 1 : length( sita ) 22 x(j,i) = x0 + a * sin( psi(j) ) * cos( sita(i) ); 23 y(j,i) = y0 + b * sin( psi(j) ) * sin( sita(i) ); 24 z(j,i) = z0 + c * cos( psi(j) ); 25 end 26 end 27 28 %% 椭圆旋转 方法一:按照展开式,不借助函数, Z-Y-X 体系 29 sita_x = pi/3; 30 sita_y = pi/6; 31 sita_z = pi/5; 32 33 q = zeros(1,4); 34 q(1) = cos( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * cos( 0.5 * sita_z ) + sin( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 35 q(2) = sin( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * cos( 0.5 * sita_z ) - cos( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 36 q(3) = cos( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * cos( 0.5 * sita_z ) + sin( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 37 q(4) = cos( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * sin( 0.5 * sita_z ) - sin( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * cos( 0.5 * sita_z ); 38 39 T_rotate = zeros(3,3); 40 T_rotate(1,1) = q(1) * q(1) + q(2) * q(2) - q(3) * q(3) - q(4) * q(4); 41 T_rotate(1,2) = 2 * q(2) * q(3) - 2 * q(1) * q(4); 42 T_rotate(1,3) = 2 * q(1) * q(3) + 2 * q(2) * q(4); 43 T_rotate(2,1) = 2 * q(1) * q(4) + 2 * q(2) * q(3); 44 T_rotate(2,2) = q(1) * q(1) - q(2) * q(2) + q(3) * q(3) - q(4) * q(4); 45 T_rotate(2,3) = 2 * q(3) * q(4) - 2 * q(1) * q(2); 46 T_rotate(3,1) = 2 * q(2) * q(4) - 2 * q(1) * q(3); 47 T_rotate(3,2) = 2 * q(1) * q(2) + 2 * q(3) * q(4); 48 T_rotate(3,3) = q(1) * q(1) - q(2) * q(2) - q(3) * q(3) + q(4) * q(4); 49 50 x1 = zeros(size(x)); 51 y1 = zeros(size(y)); 52 z1 = zeros(size(z)); 53 54 for j = 1:size(x,1) 55 for i = 1:size(x,2) 56 p = [ x(j,i) - x0, y(j,i) - y0, z(j,i) - z0 ]; 57 x1(j,i) = x0 + T_rotate(1,1) * p(1) + T_rotate(1,2) * p(2) + T_rotate(1,3) * p(3); 58 y1(j,i) = y0 + T_rotate(2,1) * p(1) + T_rotate(2,2) * p(2) + T_rotate(2,3) * p(3); 59 z1(j,i) = z0 + T_rotate(3,1) * p(1) + T_rotate(3,2) * p(2) + T_rotate(3,3) * p(3); 60 end 61 end 62 63 %% 椭圆逆向归位,方法一:按照展开式,不依赖函数,X-Y-Z 体系 64 sita_x = -sita_x; 65 sita_y = -sita_y; 66 sita_z = -sita_z; 67 68 q = zeros(1,4); 69 q(1) = cos( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * cos( 0.5 * sita_z ) - sin( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 70 q(2) = sin( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * cos( 0.5 * sita_z ) + cos( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 71 q(3) = cos( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * cos( 0.5 * sita_z ) - sin( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * sin( 0.5 * sita_z ); 72 q(4) = cos( 0.5 * sita_x ) * cos( 0.5 * sita_y ) * sin( 0.5 * sita_z ) + sin( 0.5 * sita_x ) * sin( 0.5 * sita_y ) * cos( 0.5 * sita_z ); 73 74 T_rotate = zeros(3,3); 75 T_rotate(1,1) = q(1) * q(1) + q(2) * q(2) - q(3) * q(3) - q(4) * q(4); 76 T_rotate(1,2) = 2 * q(2) * q(3) - 2 * q(1) * q(4); 77 T_rotate(1,3) = 2 * q(1) * q(3) + 2 * q(2) * q(4); 78 T_rotate(2,1) = 2 * q(1) * q(4) + 2 * q(2) * q(3); 79 T_rotate(2,2) = q(1) * q(1) - q(2) * q(2) + q(3) * q(3) - q(4) * q(4); 80 T_rotate(2,3) = 2 * q(3) * q(4) - 2 * q(1) * q(2); 81 T_rotate(3,1) = 2 * q(2) * q(4) - 2 * q(1) * q(3); 82 T_rotate(3,2) = 2 * q(1) * q(2) + 2 * q(3) * q(4); 83 T_rotate(3,3) = q(1) * q(1) - q(2) * q(2) - q(3) * q(3) + q(4) * q(4); 84 85 x3 = zeros(size(x)); 86 y3 = zeros(size(y)); 87 z3 = zeros(size(z)); 88 89 for j = 1:size(x,1) 90 for i = 1:size(x,2) 91 p = [ x1(j,i) - x0, y1(j,i) - y0, z1(j,i) - z0 ]; 92 x3(j,i) = x0 + T_rotate(1,1) * p(1) + T_rotate(1,2) * p(2) + T_rotate(1,3) * p(3); 93 y3(j,i) = y0 + T_rotate(2,1) * p(1) + T_rotate(2,2) * p(2) + T_rotate(2,3) * p(3); 94 z3(j,i) = z0 + T_rotate(3,1) * p(1) + T_rotate(3,2) * p(2) + T_rotate(3,3) * p(3); 95 end 96 end 97 98 %% 图像显示 99 figure 100 hold on 101 axis equal 102 axis off 103 104 quiver3( 0, 0, 0, 10, 0, 0, 'k', 'filled', 'linewidth', 3 ) 105 text( 10, 0, 0, 'it X', 'fontsize', 13, 'fontweight', 'bold' ) 106 quiver3( 0, 0, 0, 0, 12, 0, 'k', 'filled', 'linewidth', 3 ) 107 text( 0, 12, 0, 'it Y', 'fontsize', 13, 'fontweight', 'bold' ) 108 quiver3( 0, 0, 0, 0, 0, 10, 'k', 'filled', 'linewidth', 3 ) 109 text( 0, 0, 10, 'it Z', 'fontsize', 13, 'fontweight', 'bold' ) 110 111 % 原始椭圆 112 surf( x, y, z, 'facecolor', [0.8 0.8 0.8] ); 113 % 方法一旋转 114 surf( x1, y1, z1, 'facecolor', [0.5 0.5 0.5] ); 115 % 方法一逆旋转 116 surf( x3, y3, z3, 'facecolor', [0.7 0.5 0.3] );
