Codeforces 918D MADMAX 图上dp 组合游戏

题目链接

题意

给定一个 (DAG)，每个边的权值为一个字母。两人初始各占据一个顶点（可以重合），轮流移动（沿着一条边从一个顶点移动到另一个顶点），要求每次边上的权值 (geq) 上一次的权值。无法移动者输。

要求：对所有可能的初始情况，给出一张胜负表。

思路

特殊情况

1. 两人在同一个顶点上，那么必然是先手输；

2. 如果有(u ightarrow v)边，并且先手在 (u) 上，后手在 (v) 上，且先手此时可以移动（判断边的权值），那么必然是先手赢

一般情况

考虑用 (dp[u][v][w]) 表示先手在 (u)，后手在 (v)，上一次移动的权值为 (w) 时，先手能否移动。

如果有 (u ightarrow x) 可行（权值(wwgeq w)） 且 (dp[v][x][ww]==false)，那么意味着先手只要走到 (x)，后手就无路可走了。因此，先手有必胜策略；否则先手必败。

因为是 (DAG)，所以可以用记忆化搜索。

联想

其实这里如果联想到 组合游戏 就很好理解了。

如果一个状态的所有后继都是先手必胜态(N)，那么这个状态是先手必败态(P)。

如果一个状态能走到某一个先手必败态(P)，那么这个状态就是先手必胜态(N)。

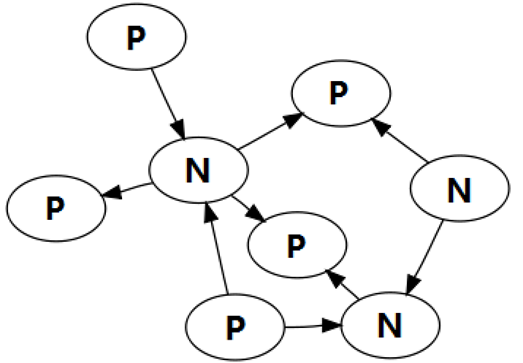
如果不考虑搜索复杂度的话，组合游戏其实也就是：在给定的DAG上确定状态是P态还是N态。而这道题恰好点数比较少，故真的就可以直接搜索了。

Code

#include <bits/stdc++.h>
#define maxn 110
#define maxm 5010
using namespace std;
typedef long long LL;
int mp[maxn][maxn];
int ne[maxn], tot;
struct Edge { int to, ne, w; }edge[maxm << 1];
bool vis[maxn][maxn][26], dp[maxn][maxn][26];
void add(int u, int v, int c) {
    edge[tot] = {v, ne[u], c};
    ne[u] = tot++;
}
int dfs(int u, int v, int ch) {
    if (vis[u][v][ch]) return dp[u][v][ch];
    vis[u][v][ch] = true;
    if (u == v) return false;
    if (mp[u][v]) {
        if (ch <= mp[u][v]) return dp[u][v][ch] = true;
    }
    for (int i = ne[u]; ~i; i = edge[i].ne) {
        int x = edge[i].to; char ww = edge[i].w;
        if (ch <= ww && !dfs(v, x, ww)) return dp[u][v][ch] = true;
    }
    return false;
}
int main() {
    memset(ne, -1, sizeof ne);
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; ++i) {
        int u, v; char c;
        scanf("%d%d %c", &u, &v, &c);
        mp[u][v] = c-'a';
        add(u, v, c-'a');
    }
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            putchar(dfs(i, j, 0) ? 'A' : 'B');
        }
        puts("");
    }
    return 0;
}