时隔多日的又一道dp(状压dp)
Southern and Volga Russia Qualifier 2019-2020C. Marbles
pof说:
那个啊,因为他最后肯定都是一团一团的嘛,
然后a[i]最大只有20,
所以直接状压dp[s]
表示已经把二进制下为1的块按最优顺序放到数列最前面的最少花费
/////pofnb
#include<bits/stdc++.h> #include<tr1/unordered_map> #define debug printf("!"); using namespace std; typedef long long ll; typedef unsigned long long ull; const int inf=0x3f3f3f3f; const int maxn=4e5+5; /* pof: 那个啊,因为他最后肯定都是一团一团的嘛, 然后a[i]最大只有20, 所以直接状压dp[s] 表示已经把二进制下为1的块按最优顺序放到数列最前面的最少花费 */ ll dp[2000004]; ll num[22]={0},fnum[22][22]={0},up,resta; int ha[22]={0}; //num是记录当前的数的个数,方便计算dp1 //fnum[u][v]是记录如果 v这一团在u的前面 则把v这一团移到u前所用的步数 //ha是把离散序列化为连续序列 int main() { int n,i,j,k,tot,a; memset(dp,inf,sizeof(dp)); memset(ha,-1,sizeof(ha)); scanf("%d",&n); for(i=1;i<=n;i++) { scanf("%d",&a); if(ha[a]!=-1)a=ha[a]; else { ha[a]=up++; a=ha[a]; } resta|=(1<<a); if(!num[a]) { dp[1<<a]=0; } dp[1<<a]+=i-num[a]-1; num[a]++; for(j=0;j<20;j++)fnum[a][j]+=num[j]; } dp[0]=0; int now[22]; ll sum; for(i=1;i<(1<<up);i++) { for(j=0,tot=0;j<up;j++) { if(!(i&(1<<j)))continue; now[tot++]=j; } for(j=0;j<tot;j++) { sum=0; for(k=0;k<tot;k++) { if(k==j)continue; sum+=fnum[now[j]][now[k]]; } dp[i]=min(dp[i],dp[i^(1<<now[j])]+dp[1<<now[j]]-sum); } } printf("%lld ",dp[(1<<up)-1]); }
2019-09-25 19:23:00
每日一dp 又是dp
Southern and Volga Russia Qualifier 2019-2020H. Berland Prospect
求最长的等差数列
以为距离是longlong不能用dp但是忘记有map
#include<cstdio> #include<algorithm> #include<tr1/unordered_map> #define debug printf("!"); using namespace std; typedef long long ll; const int maxn=3e3+50; const int mod=1e9+7; const int inf=0x3f3f3f3f; tr1::unordered_map<int,ll>dp[maxn]; int main() { int n,i,j,k,ans=1,num; ll a[maxn],dis; scanf("%d",&n); for(i=1;i<=n;i++)scanf("%lld",&a[i]); for(i=1;i<=n;i++) { for(j=i-1;j>0;j--) { dis=a[i]-a[j]; k=dp[i][dis]=dp[j][dis]+1; ans=max(ans,k); } } printf("%d ",ans+1); }
还差得远,继续练QAQ
2019-09-19 19:30:11
T个询问 输出长度为n的第k个Rhyme scheme;贝尔数
还是不太懂dp是什么
题解说这种做法是dp,那就是dp吧
/*
题解说:
• 如右图,Rhyme scheme可以形成一个字典树。(图为n=3)
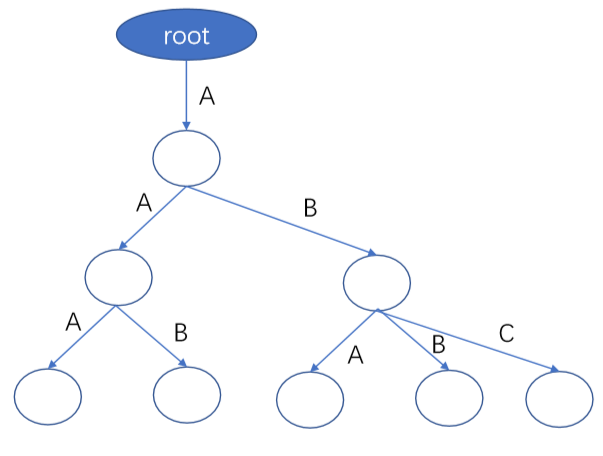
• 可以用DP求出,dp[n][i][j]表示长度为n的Rhyme scheme, 在第i层, 前面出现的字母最大是j有多少个。
• 如果询问n,k的时候,只要在字典树上从上往下走即可。
• B(26)会超出long long, 可以用两个long long或者__int128搞一搞
*/
然后我看懂了dp[n][i][j]。然后题解代码的做法看不懂。然后我结合dp思路用了自己的做法:
首先:
设dp[u][i][j]表示:起始字母为u的树,在第i层的Rhythm scheme(下面简称Rs),最大字母为j 的数 有多少个
按题意,其始字母一定是A,设长度为n;
如果看子树,把子树看成一棵独立的树,以它为根,有新的Rs,长度为n-k,k为根的层数-1,而起始字母就不一定是A了。所以有了[u]这个单元,作用如下:
此时设sum[u][i],表示起始字母为u的数,在第i层(长度为i)的Rs的个数,则sum[u][i]=∑dp[u][i][j](1<=j<=i)。
dp的作用是为了求出sum,用sum数组来找到答案。
dp[u][][]对下一个u无影响。可以略去,便是dp[i][j]。
那么,题目的答案输出就可以是:
判断输出字母在当前层数之后的Rs的数目,如果大于k,就减去这颗树的大小,直到小于等于k,输出这个字母。然后再在下一层遍历一遍。
然而,这种做法会出错。
因为以u节点为根子树,并一定不等于以u开始建的Rs数。因为:
以u节点为根的子树,上面可能有比u节点大的字母,设为其上最大字母为up,此时,u节点的拓展不是[1,u+1],而是[1,up+1],
所以,对新建的子树做修改,拓展出up单元,表示整棵树的【最小*最大字母*】是up,然后在up的基础上,以建立u节点开头的树,就其到达每层的Rs的个数。
sum[up][u][i]。
结论:答案的结果是记录当前以输出的最大字母up,从1开始遍历字母c,判断k和sum[up][c][i]的关系,大于则减去,小于等于则跳出循环,输出。更新最大字母。
#include<bits/stdc++.h> #define debug printf("!"); using namespace std; typedef long long ll; const int maxn=1e5+50; const int mod=1e9+7; const int inf=0x3f3f3f3f; void read(__int128 &x) { char ch; while(!isdigit(ch=getchar())); x=ch-'0'; while(isdigit(ch=getchar())) x=x*10+ch-'0'; } /* dp[i][j] 第i层 前面出现的字母 最大是j 的 Rhyme scheme 有多少个? dp[i][j]=dp[i-1][j]*j+dp[i-1][j-1]; */ __int128 dp[27][27],sum[27][27][27]; void init() { int i,u; __int128 j,up,t; for(up=1;up<=26;up++) { memset(dp,0,sizeof(dp)); for(u=1;u<=26;u++) { dp[1][up]=sum[up][u][1]=1; for(i=2;i<=26-u+1;i++) { sum[up][u][i]=0; for(j=up;j<=up+i-1&&j<=26;j++) { dp[i][j]=dp[i-1][j]*j+dp[i-1][j-1]; sum[up][u][i]=sum[up][u][i]+dp[i][j]; } } } } } int main() { init(); int T,u; scanf("%d",&T); for(u=1;u<=T;u++) { int n,i,j,c,up; __int128 k; scanf("%d",&n); read(k); printf("Case #%d: ",u); up=1; for(i=1;i<=n;i++) { for(c=1;c<up&&k>sum[up-1][c][n-i+1];c++)k-=sum[up-1][c][n-i+1]; putchar('A'+c-1); up=max(up,c+1); } putchar(10); } }
2019-09-18 12:56:05
每日dp
题意:给定一行n个非负整数a[1]..a[n]。现在你可以选择其中若干个数,但不能有超过k个连续的数字被选择。使得选出的数字的和最大。
原本做法是O(nk) 也就是O(n^2) 90分 超时了
后来写一个简单的线段树维护区间最小值 过了
然后题解更优的做法是单调队列维护区间最小值。 忘记简单维护区间的最小值单调队列更方便了。
#include<bits/stdc++.h> #define debug printf("!"); using namespace std; typedef long long ll; const int maxn=1e5+50; const int mod=1e9+7; const int inf=0x3f3f3f3f; /* 不能超过k个数连续 [5 6 7 4] 9 [3 2 11 9] 2 [4 3 6 5 [6 7 4 9] 3 [2 11 9] 2 [4 3 6 [5 6 7] 4 [9 3] 2 [11 9] 2 [4 3 6 [5 6 7 4] 9 [11 12 13 14] 4 [3 2 1 */ /* dp[i]表示删除了第i个数 dp[i]=min(dp[i-j]+a[i],dp[i])//i-k-1<=j<i O(n^2) */ const ll INF=LLONG_MAX>>1; int main() { int n,k,i,j; ll a[maxn],dp[maxn],sum=0,ans=0,que[maxn],fir,tail; scanf("%d%d",&n,&k); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); sum+=a[i]; } a[0]=0;fir=0,tail=-1; for(i=0;i<=n;i++) { if(i-k-1<=0) { dp[i]=a[i]; while(fir<=tail&&dp[que[tail]]>=dp[i])tail--; que[++tail]=i; } else { while(fir<=tail&&que[fir]<i-k-1)fir++; dp[i]=dp[que[fir]]+a[i]; while(fir<=tail&&dp[que[tail]]>=dp[i])tail--; que[++tail]=i; } if(i>=n-k)ans=max(ans,sum-dp[i]); } printf("%lld ",ans); }
也是今天遇到的题比较简单,也也许是我进步一点点了。
2019-09-17 21:42:47
退背包。
按题解说:
• 对所有石子从大到小排序,进行dp。
• 我们考虑取出的那一堆石子,f[i][j] 表示该堆石子里最小的石子为 i,总价值 为 j 的方案数,这个通过dp来算。
• 对于所有最小石子为 i 的方案,可以求出其左右边界,那么对应答案加上改 区间内的 f[i][l] ~ f[i][r]。其中 i 这一维可以略去。
所以当前的*最小的石子*为必取,比当前的*最小的石子*小的石子必不取
所以先退最小的石子,把此时退的石子当做必取,统计除去这个石子外满足价值总和为m的方案数:退背包。最初的更新数组就是背包数组。
退完上一颗石子就退当前石子,设当前石子为必取石子,比当前小的石子已退。所以用上一次的dp数组作为这一次的更新数组。
然后每一次(退完一颗石子==必取一颗石子),就按照当前石子的左右边界累加答案。
因为是从小到大退石子,所以需要排序。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int mod=1e9+7; const int manx=1e5+50; //f[i][j]=max(f[i][j],f[i][j-v]+1) int main() { int T; scanf("%d",&T); while(T--) { int n,i,j,a[330],sum=0; ll dp[150005]={0},ans=0; scanf("%d",&n); for(i=1;i<=n;i++) { scanf("%d",&a[i]); sum+=a[i]; } sort(a+1,a+1+n); dp[0]=1; for(i=1;i<=n;i++) for(j=sum;j>=a[i];j--) dp[j]=(dp[j]+dp[j-a[i]])%mod; for(i=1;i<=n;i++) { for(j=a[i];j<=sum;j++) dp[j]=(dp[j]-dp[j-a[i]]+mod)%mod; for(j=max((sum+1)/2-a[i],0);j<=sum-j-a[i];j++) ans=(ans+dp[j])%mod; } printf("%lld ",ans); } }
每日一dp 退背包
我才知道背包还能退的。
题意是 :有 N 个物品, 体积分别是 W1, W2, …, WN。 第 i 个物品丢失了。 要使用剩下的 N – 1 物品装满容积为 x 的背包,有几种方法呢?
!!!!!
背包:f[i][j] = f[i-1][j-w[i]] + f[i-1][j]
退背包:f[i-1][j] = f[i][j] - f[i-1][j-w[i]] (先求出背包的dp数组!!!!)
然后据说:转移的时候带系数的背包不一定可以退背包
////背包 for(i=1;i<=n;i++) for(j=w[i];j<=m;j++) f[i][j]=f[i-1][j-w[i]]+f[i-1][j]; //优化: for(i=1;i<=n;i++) for(j=m;j>=w[i];j--) f[j]=f[j]+f[j-w[i]]; ////退背包 for(i=1;i<=n;i++) for(j=m;j>=w[i];j--) f[i-1][j]=f[i][j]-f[i-1][j-w[i]]; //优化 for(i=1;i<=n;i++) for(j=w[i];j<=m;j++) f[j]=f[j]-f[j-w[i]];
//完全背包退背包 (先dp出完全背包) for(i=m;i>=w[x];i--)dp[i]-=dp[i-w[x]];
求最小花费使得重量达到m或以上
物品可以无限量取。
不会做dp还要现场做。搞得好紧张啊.......
#include<bits/stdc++.h> #define debug printf("!"); using namespace std; typedef long long ll; const int maxn=5e4+50; const int inf=0x3f3f3f3f; const int mod=1e9+7; struct P{ int p,w; }b[maxn]; int main() { int n,m,i,j,k,up=0,v,ans1,ans2; while(~scanf("%d%d",&n,&m)) { for(i=1;i<=n;i++) { scanf("%d%d",&b[i].p,&b[i].w); up=max(up,b[i].w); } int dp[maxn]; memset(dp,inf,sizeof(dp)); dp[0]=0; for(i=0;i<=m+up;i++) { for(j=1;j<=n;j++) { if(i>=b[j].w)dp[i]=min(dp[i],dp[i-b[j].w]+b[j].p); } } ans1=inf,ans2=inf; for(i=m;i<=m+up;i++) { if(dp[i]<=ans1) { ans1=dp[i]; ans2=i; } } // printf("$%d ",m+up); printf("%d %d ",ans1,ans2); } }
每日一dp
重点在题解的路径压缩。
题解说:
每次走p步或者 p+1p+1 步,p*(p+1)p∗(p+1) 之后的地方均能够到达。
如果两个石子之间的距离大于 p*(p+1)p∗(p+1) ,那么就可以直接将他们之间的距离更改为 p*(p+1)p∗(p+1)
#include<bits/stdc++.h> #define debug printf("!"); using namespace std; typedef long long ll; const int maxn=3e5+50; const int inf=0x3f3f3f3f; //dp[i+j]=min(dp[i+j],dp[i]+is[i+j]) int main() { int L,s,t,m,i,j,k,ans; int is[20200]={0},dp[20200],a[110],dis; scanf("%d",&L); scanf("%d%d%d",&s,&t,&m); if(s==t) { ans=0; for(i=1;i<=m;i++) { scanf("%d",&k); if(k%s==0)ans++; } printf("%d ",ans); return 0; } for(i=1;i<=m;i++) scanf("%d",&a[i]); sort(a+1,a+1+m); k=0;a[0]=0; for(i=1;i<=m;i++) { dis=min(a[i]-a[i-1],90); k+=dis; is[k]=1; } dis=min(L-a[m],100); L=k+dis; dp[0]=0; for(i=s;i<=L+10;i++) { dp[i]=200; for(j=s;j<=t ;j++) if(i>=j)dp[i]=min(dp[i],dp[i-j]+is[i]); } ans=dp[L]; for(i=L;i<=L+10;i++)ans=min(ans,dp[i]); printf("%d ",ans); }
2018-2019 ACM-ICPC Brazil Subregional Programming Contest
我这才知道原来cf 1s 可以跑1e9
也许不止.... 试了86400*2047...=1e9+...然后300+ms...
比赛的时候想到了dp 也想到了状压 也想到了一层时间一层状态...
然后 然后我以为要离散 发现处理好麻烦... 然后就去看L了.....
然后 然后不用离散啊... 然后大概不用离散我当时也未必就能做出来QAQ.. dp太弱了
#include<cstdio> #include<cstring> #include<vector> #include<bitset> #include<algorithm> #define debug printf("!"); using namespace std; typedef __int64 ll;//%I64d struct P{ int s,t,v,id; bool operator <(const P&p)const{return t<p.t;} P(int ss,int tt,int vv,int idd){s=ss;t=tt;v=vv;id=idd;} }; int dp[86440][2100]; int main() { int n,m,i,j,k,num,a,ans=0,s,t,v,tot,id,up=0,siz; vector<P> p; scanf("%d",&n); for(i=0;i<n;i++) { scanf("%d",&num); for(j=1;j<=num;j++) { scanf("%d%d%d",&s,&t,&v); p.push_back(P(s,t,v,i)); up=max(up,t); } } sort(p.begin(),p.end()); memset(dp,0,sizeof(dp)); tot=0;siz=p.size(); for(i=1;i<=up;i++) { if(tot==siz)break; for(j=1;j<(1<<n);j++)dp[i][j]=dp[i-1][j]; if(i<p[tot].t)continue; while(p[tot].t==i) { dp[i][1<<p[tot].id]=max(dp[i][1<<p[tot].id],p[tot].v); for(j=1;j<(1<<n);j++) { if(!dp[p[tot].s][j])continue; dp[i][j|(1<<p[tot].id)]=max(dp[i][j|(1<<p[tot].id)],dp[p[tot].s][j]+p[tot].v); } tot++; if(tot==siz)break; } } if(!dp[up][(1<<n)-1])printf("-1 "); else printf("%d ",dp[up][(1<<n)-1]); }
2019-09-12 23:34:56
第一次正式接触区间dp,以前应该遇见过,但没这个意识。
“区间DP,顾名思义是在区间上DP,它的主要思想就是先在小区间进行DP得到最优解,然后再利用小区间的最优解合并求大区间的最优解。”
然后看了区间dp的套路,做出这道题了。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int mod=1e9+7; const int maxn=1e3+50; ll dp[maxn][maxn][2]; //dp[i][j][0] [i,j]以j为最后一个入队的人的种数 //dp[i][j][1] [i,j]以i为最后一个入队的人的种数 int main() { memset(dp,0,sizeof(dp)); int n,i,j,len,p=19650827; ll a[maxn]; scanf("%d",&n); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); dp[i][i][0]=1; } for(len=2;len<=n;len++) { for(i=1;i+len-1<=n;i++) { j=i+len-1; if(len==2) { if(a[j-1]<a[j])dp[i][j][0]=dp[i][j-1][0]; if(a[i+1]>a[i])dp[i][j][1]=dp[i+1][j][0]; continue; } if(a[j-1]<a[j])dp[i][j][0]=dp[i][j-1][0]%p; if(a[i]<a[j])dp[i][j][0]=(dp[i][j][0]+dp[i][j-1][1])%p; if(a[j]>a[i])dp[i][j][1]=dp[i+1][j][0]%p; if(a[i+1]>a[i])dp[i][j][1]=(dp[i][j][1]+dp[i+1][j][1])%p; } } printf("%lld ",(dp[1][n][0]+dp[1][n][1])%p); }
2019-09-10 13:29:20