二分算法

　　1. 基本介绍

二分思想一般用于查找，见其名知其意，这是一个半半开的算法。第一次接触二分思想的时候是高中的数学学习中，给定一个方程 f(x) = 0的根所在的区间，可以用根存在定理不断二分区间，当区间长度小于给定的精度时，即可近似求出方程的解，当然也可以用来求平方根和立方根等。同样，这种查找思想也可以运用于计算机内结构化数据的查找。（tips: 二分查找思想简单，细节魔鬼）。(详讲博客推荐)

二分查找有很多应用，由于其时间复杂度很低，它可以暴力破解很大的数据。

2. 核心思想

使用二分查找的前提：待查找序列必须有序（升序或降序，本文主要以升序为例）

确定查找区间(left, right)，取区间中间值mid = (left + right)/2，比较中间值与左右两边的值，确定待查元素key所在区间，舍弃无效区间(mid = left 或mid = right)。

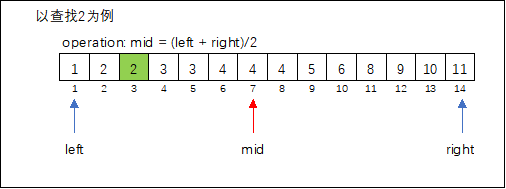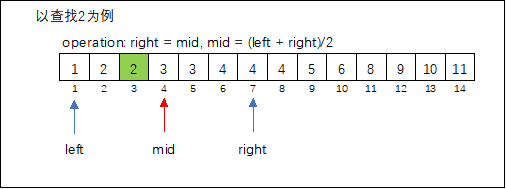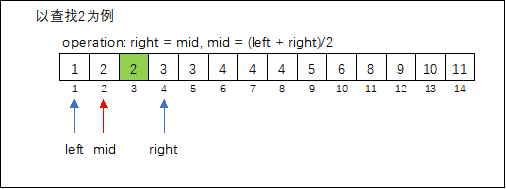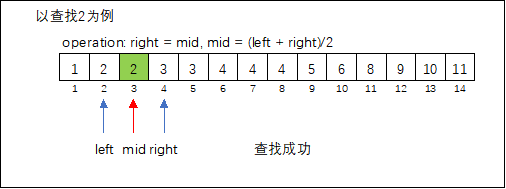
3. 算法效率分析

时间复杂度：对于数据规模n，每次二分会使查找区间长度减半。最好情况只需要一次查找即可，最坏情况要找()次。综上述，二分算法其渐进时间复杂度为O()。所以，很多地方考查找时卡时间复杂的时候就要考虑使用二分啦。

       空间复杂度：没有使用额外空间，比较友好。

4. 代码实现

• 朴素实现

int BinaryChop(int *arr, int len, int key) {
    int left = 0, right = len, mid;
    while (left < right) {
        mid = (left + right) / 2;
        if (arr[mid] == key)
            return mid; // 找到返回元素位置
        else if (arr[mid] > key)
            right = mid - 1;
        else
            left = mid + 1;
    }
    return -1;// 没找到返回-1
}

• 通用实现

int search(int k) {
    int l = -1,r = n;//注意的是数组是从0开始的
    while(l + 1 < r) {
        int mid = l + r >> 1;
        if(a[mid] <= k)
            l = mid;
        else 
            r = mid;
    }
    return r;//返回的是大于k的第一个位置
}

• C++中STL内的函数

lower_bound(begin, end, num)：从数组的begin位置到end-1位置二分查找第一个大于等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound(begin, end, num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

5. 习题链接

　　https://www.luogu.com.cn/problem/P2249 P2249 【深基13.例1】查找

　　https://www.luogu.com.cn/problem/P1102 P1102 A-B 数对

　　https://www.luogu.com.cn/problem/P1024 P1024 [NOIP2001提高组]一元三次方程求解

　　https://www.luogu.com.cn/problem/P1678 P1678 烦恼的高考志愿

　　https://www.luogu.com.cn/problem/P2440 P2440 木材加工

　　http://120.78.128.11/Problem.jsp?pid=2145 二分法模板

　　http://120.78.128.11/Problem.jsp?pid=1762 杯子

　　http://120.78.128.11/Problem.jsp?pid=2366 二分强化——全面查询

　　http://120.78.128.11/Problem.jsp?pid=2446 Champion_Q的魔法蛋糕

　　https://www.luogu.com.cn/problem/P2678 P2678 [NOIP2015 提高组] 跳石头

　　https://www.luogu.com.cn/problem/P3853 P3853 [TJOI2007]路标设置

　　我的题解：

　　洛谷-P2249 【深基13.例1】查找 - Kirk~~ - 博客园 (cnblogs.com)

　　洛谷-P1102 A-B 数对 - Kirk~~ - 博客园 (cnblogs.com)

　　洛谷-P1024 [NOIP2001 提高组] 一元三次方程求解 - Kirk~~ - 博客园 (cnblogs.com)