D
Content
· 问题回溯
· 问题分析
· 可行代码
· 总结
(一) 问题回溯
DESCRIPTION

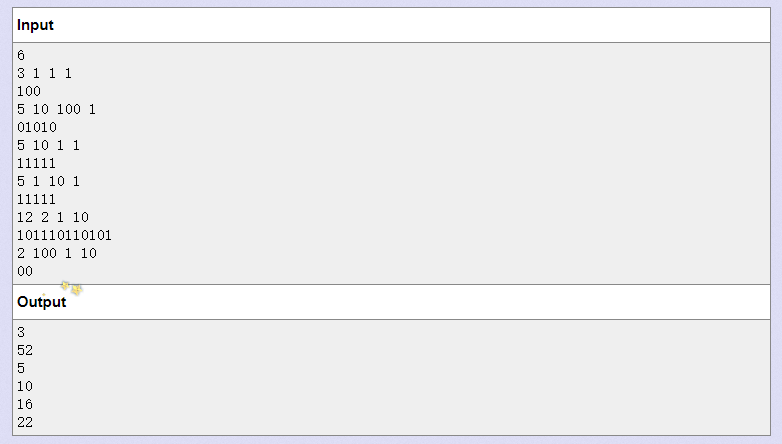
INPUT

OUTPUT

EXAMPLE
NOTE
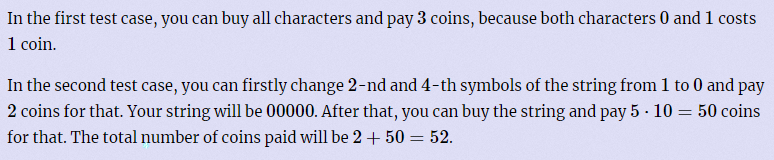
(二)问题分析
由题可知,最终价格由两部分组成 —— 交换价格(换1 + 换0)和购买价格(买0 + 买1)
可以通过枚举的方法,枚举每种交换搭配后的价格,取其最小值。
令 (0 -> 1) 共 i 个,(1 -> 0) 共 j 个 ,每次交换后的总价为price,最初总共有num0个 '0' 、num1个 '1'
总价 = 交换价格 + 购买价格 --> price = ( i + j ) * h + ( num0 + j - i ) * c0 + ( num1 + i - j ) * c1
整理得 price = i * ( h - c0 + c1 ) + j * ( h + c0 - c1 ) + num0 * c0 + num1 * c1
(三)可行代码
#include <iostream> using namespace std; int main(){ int T; cin >> T; while (T--){ int n, c0, c1, h; cin >> n >> c0 >> c1 >> h; int num0 = 0, num1 = 0; char arr[n]; for (int i = 0; i < n; i++){ cin >> arr[i]; arr[i] == '1' ? num1++ : num0++; } int MinPrice = num0 * c0 + num1 * c1, MaxPrice = MinPrice; for (int i = 0; i <= num0; i++){ for (int j = 0; j <= num1; j++){ int price = MaxPrice + i * (h - c0 + c1) + j * (h + c0 - c1); if(price < MinPrice && price > 0) // 可能会出现负数情况 MinPrice = price; } } cout << MinPrice << endl; } return 0; }
(四)总结
做题前先推公式会事半功倍,题目注意要点,i 与 j 的变化会导致两方价格都变化(开始我就只算了一边),公式中出现的负数情况要注意排除