<本人比较喜欢做总结,所以许多的知识都是从网上找到的并且重新组织利用,主要目的是为了加深我个人的理解和总结,欢迎大家指出错误,一起讨论,一起进步>
资料参考:https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86
“有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?”这就是中国剩余定理的来源了,什么意思呢?就是说数一堆物品,如果三个三个数的话,就会剩下二个,如果五个五个数的话,就会剩下三个,如果是七七数的话,就会剩下二个,那么到底有多少个呢?(来源wiki)
我想从特殊到一般来讨论这个问题;
题目其实可以抽象来数学问题如下: 现在我们想想,如何才能找到这么一个数x呢?
现在我们想想,如何才能找到这么一个数x呢?
首先我们定义a[1 2 3] = 2, 3, 2;m[1 2 3] = 3, 5, 7; 我们思考下,如果存在这么一个x的话,那么它有什么性质呢?首先它要满足被mi取模时其对应的值为ai,好那么我们从编程中的循环来思考,是否存在那么一个Ti使得对于Ti % mi = ai,同时Ti % mj(j != i) = 0 如果存在的话,那么我们x 就可以等于 T1 + T2 + T3 (因为可以把模分别分配到Ti上,有两个值为0)有的话,又要怎么构造?好, 起码我们现在有一思路了。那么Ti怎么构建,首先一定有一个 ai % mi = ai,那么我们可以找一个Ti/ai ,它满足Ti/ai % mi = 1,同时由Ti % mj(j != i) = 0、 Ti/ai % mi = 1、Ti % mi = ai可以得到这个Ti/ai 这个项有一个性质 Ti/ai % mj = 0;好了现在关于
Ti/ai这个项已经有了一定的性质:Ti/ai % mj =0, Ti/ai % mi = 1,故通过构造令Ti/ai是mj的倍数,同时,它会是在mi下两个互为倒数的乘积,所以用取Mi 为mi的累乘,但排除第i项目,同时令ti = Mi 模 mi 的数论倒数,也即满足ti * Mi = 1 (mod mi), Ti/ai = ti * Mi;
(这里要补充下说明,什么是模mi的数论倒数,也就是说当Mi确定的时候,可以通过 ti * Mi % mi == 1这个判断的数字,这个可以循环来求,循环的最大次数是mi,因为ti < mi,打到一个最小的ti就可以了)
那到现在确定了Ti = ai * ti * Mi,同时对于(S)我们有一个ti * Mi % mi = 1 ,也就是说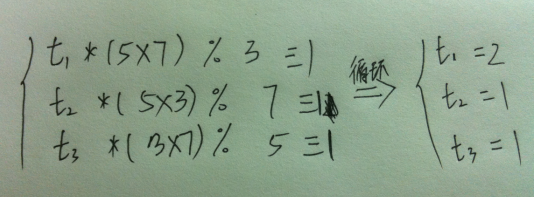
所以就可以确定T1、 T2、T3,也就可以求出X了。
对于原理的一般性证明,我觉得wiki上的证明很不错。

里面有一个要补充说明下,为什么x1 - x2 ==0 (mod mi) 而且两两mi之间互质就可以推出两解之间相关M的整数倍 呢?是因为x1 - x2 == 0 (mod mi)就表明了x1 - x2
起码有全部的mi作为约数(上面等式的成立是针对全部的mi来说的),同时M又是全部mi的乘积,所以就可以得到x1 - x2 是M的倍数,x1 - x2 <= M(假设x1 > x2)
推荐题目练习:POJ 1006