按常规,先说一下我自己的理解。
递归中的return常用来作为递归终止的条件,但是对于返回数值的情况,要搞明白它是怎么返回的。递归的方式就是自己调用自己,而在有返回值的函数中,上一层的函数还没执行完就调用下一层,因此,当达到递归终止条件时,首先return的是最底层调用的函数,return之后,继续执行上一层调用该函数之后的代码,此时我们看到的是上一层的情况,当上一层剩余的代码执行完之后,表示上一层的函数也结束,此时再返回上上一层,执行递归代码之后的代码,如此往复循环,直到返回到最上层,结束整个递归过程。需要注意的是,上一层执行递归之后的代码的时候,会调用下一层返回的值,也可以理解为在执行上一层代码的时候会调用下一层的实现过程,直到下一层执行完返回一个数值,然后再加上上一层的数值,就构成了上一层return的东西,如此往复。
注意这个return,return是返回上一层,而不是跳出回到主函数。
然后如果不是return,在当前层没有可以执行的东西的时候,也跳回到上一层。
下面我们来看算法笔记中的全排列和n皇后问题。
n皇后问题
n皇后问题是指在一个n*n的国际象棋棋盘上放置n个皇后,使得这n个皇后两两均不在同一行、同一列、同一对角线上,求合法的方案数。
(我第一反应这不是图论里的匹配嘛……也可以点着色(x)
因为如果枚举n*n种情况的位置,选择n个,计算量太大,所以我们只考虑全排列情况,然后剔掉不满足不在同一对角线上的情况。
法1:枚举
这里枚举出n长数列的全排列,然后剔掉不满足不在同一对角线上的情况。
全排列:给出1~n的数字,给出所有的排列方式(不重复)。(Ann)
递归思想:
- 递归边界:
- 递归本体:假设已经填好了P[1]~P[index-1],正准备填P[index]. 枚举x从1到n,如果hashtable[x] == false,就把它填到index中。然后递归下一位。
递归完成后,把这一位的hashtable[x]释放。
判断:到达边界(输出)的时候,判断是不是在同一对角线上。
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 11;
int n;
int P[maxn];
bool hashTable[maxn] = {false};
int cnt = 0;
void show_hashTable()
{
for (int i = 1; i <= n; i++)
{
printf("%d ", hashTable[i]);
}
printf("
");
}
void generateP(int index)
{
if(index == n+1) //递归边界,边界先判断,只算结果
{
for(int i = 1; i <= n; i++)
{
printf("%d", P[i]);
}
printf("
");
return;
// bool flag = true; //flag为true表示当前排列合法
// for(int i = 1; i <= n; i++) //遍历任意两个皇后
// {
// for(int j = i + 1; j <=n; j++)
// {
// if(abs(i - j) == abs(P[i] - P[j])) //如果在一条对角线上
// {
// flag = false; //不合法
// }
// }
// }
// if(flag) cnt++;
// return;
}
for(int x = 1; x <= n; x++)
{
printf("x %d
", x);
if(hashTable[x] == false)
{
P[index] = x;
//show_hashTable();
hashTable[x] = true;
generateP(index + 1);
hashTable[x] = false;
//show_hashTable();
}
}
}
int main()
{
scanf("%d", &n);
generateP(1);
printf("%d
", cnt);
system("pause");
}
这段代码是怎么运行的?
我实在是好奇,然后就一步一步尝试了一下。
为了方便理解起见,这里选n=3.
结果是123 132 213 231 312 321
自带字典序。
for(int x = 1; x <= n; x++)
{
printf("x %d
", x);
if(hashTable[x] == false)
{
P[index] = x;
//show_hashTable();
hashTable[x] = true;
generateP(index + 1);
hashTable[x] = false;
//show_hashTable();
}
}
我做了一个这段代码的运行原理:
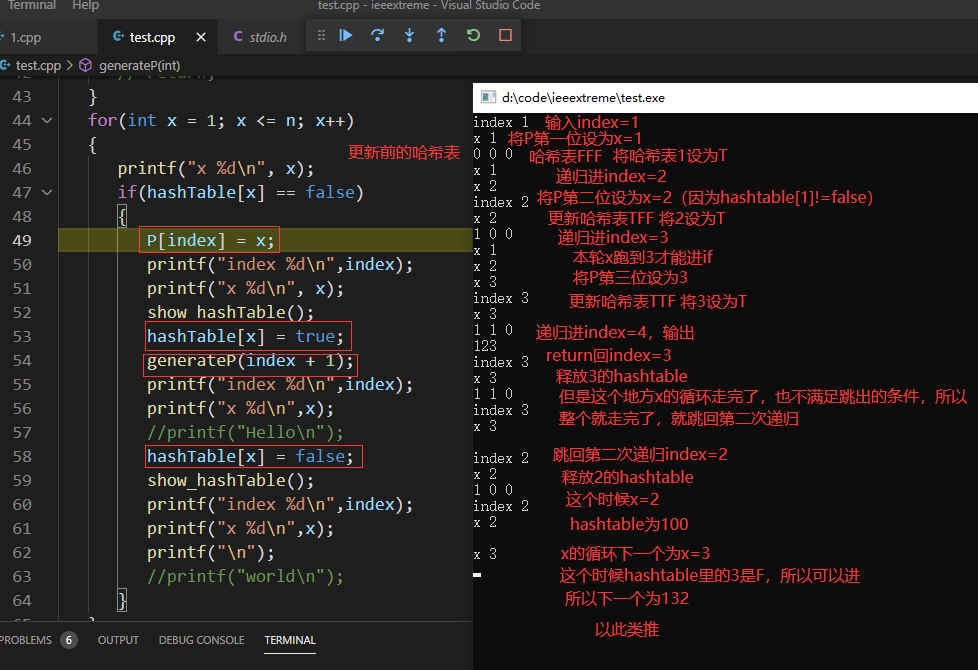
法2:回溯
定义:在到达递归前的某层,由于一些事实导致已经不需要往任何一个子问题递归,就可以直接返回上一层。
从代码编写上来看,其实就是把判断放到了递归的最开头。
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 11;
int n;
int P[maxn];
bool hashTable[maxn] = {false};
int cnt = 0;
void show_hashTable()
{
for (int i = 1; i <= n; i++)
{
printf("%d ", hashTable[i]);
}
printf("
");
}
void generateP(int index)
{
if(index == n+1) //递归边界,边界先判断,只算结果
{
for(int i = 1; i <= n; i++)
{
printf("%d", P[i]);
}
printf("
");
cnt++;
return;
// bool flag = true; //flag为true表示当前排列合法
// for(int i = 1; i <= n; i++) //遍历任意两个皇后
// {
// for(int j = i + 1; j <=n; j++)
// {
// if(abs(i - j) == abs(P[i] - P[j])) //如果在一条对角线上
// {
// flag = false; //不合法
// }
// }
// }
// if(flag) cnt++;
// return;
}
for(int x = 1; x <= n; x++)
{
//printf("x %d
", x);
if(hashTable[x] == false)
{
bool flag = true; //表示可行
for (int pre = 1; pre < index; pre++) //考察index之前的是否会与index冲突
{
if (abs(index - pre) == abs(x - P[pre]))
{
flag = false;
break; //已经设置了flag,很保险;break只是为了节约不要后面无意义的for循环
}
}
if (flag)
{
P[index] = x;
hashTable[x] = true;
generateP(index + 1);
hashTable[x] = false;
}
}
}
}
int main()
{
scanf("%d", &n);
generateP(1);
printf("%d
", cnt);
system("pause");
}