警告
此文章将耗费你成吨的流量,请wifi下阅读,造成的流量浪费本人不承担任何责任。初版源代码获取(请勿用作他用,仅供学习):https://gitee.com/kingstacker/iir.git
若有问题可以联系我邮箱:kingstacker_work@163.com
版权所有,转载请注明出处。
感谢
感谢杜勇老师的书籍:

感谢杜勇老师不厌其烦的答复我的邮件垂询。
感谢自己,编代码调试眼睛快瞎了。。。。。
前言
这个课程设计做过一年多了,知识什么的差不多都忘记了,最近去面试直接就问项目,而且问得挺细,一脸懵逼,眼泪掉下来,
简历上写的项目你自己一定要说的明白。
简历上写的项目你自己一定要说的明白。
简历上写的项目你自己一定要说的明白。
所以,又复习了一遍,当然更为娴熟也添加了新的东西。
基础知识:
什么叫滤波器?
简单的说,就像筛米,留下你需要的米,滤掉不需要的米头。过滤的功能。
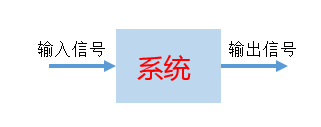
什么叫数字滤波器?
用数字芯片做的滤波器,而不是rc搭的,输入是离散的序列,输出也是离散的序列;
快速了解时域频域:
https://zhuanlan.zhihu.com/p/19763358?from=singlemessage&isappinstalled=1
什么叫时域?
信号随时间的变化。
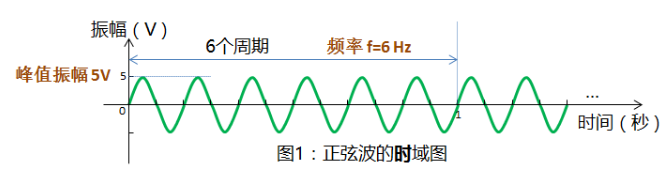
什么叫频域?
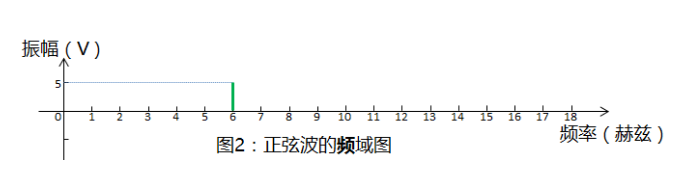
曾经有个通俗的解释是:弹钢琴,琴键1234等表示的就是频域,产生的各种音乐就是时域,你以为的万变其实是永恒的不变。
什么叫fir与iir滤波器?
FIR(Finite Impulse Response)滤波器:有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。
无限脉冲响应。递归滤波器,也就是IIR数字滤波器,顾名思义,具有反馈。
fir和iir有啥异同(important)?
根据冲激响应的不同,将数字滤波器分为有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。对于FIR滤波器,冲激响应在有限时间内衰减为零,其输出仅取决于当前和过去的输入信号值。对于IIR滤波器,冲激响应理论上应会无限持续,其输出不仅取决于当前和过去的输入信号值,也取决于过去的信号输出值。
1. 在相同技术指标下,IIR滤波器由于存在着输出对输入的反馈,因而可用比FIR滤波器较少的阶数来满足指标的要求,这样一来所用的存储单元少,运算次数少,较为经济。例如用频率抽样法设计阻带衰减为-20db的FIR滤波器,其阶数要33阶才能达到,而如果用双线性变换法设计只需4-5阶的切贝雪夫滤波器,即可达到指标要求,所以FIR滤波器的阶数要高5-10倍左右。
2. FIR滤波器可得到严格的线性相位,而IIR滤波器则做不到这一点,IIR滤波器选择性愈好,则相位的非线性愈严重,困而,如果IIR滤波器要得到线性相位,又要满足幅度滤波的技术要求,必须加全通网络进行相位校正,这同样会大大增加滤波器的阶数,从这一点上看,FIR滤波器又优于IIR滤波器。
3. FIR滤波器主要采用非递归结构,因而从理论上到实际的有限精度的运算中,都是稳定的。有限精度运算误差也较小,IIR滤波器必须采用递归的结构,极点必须在Z平面单位圆内,才能稳定,这种结构,运算中的四舍五入处理,有时会引起寄生振荡。
4. FIR滤波器,由于冲激响应是有限长的,因而可以用快速傅里叶变换算法,这样运算速度可以快得多,IIR滤波器则不能这样运算。
5. 从设计上看,IIR滤波器可以利用模拟滤波器设计的现成闭合公式、数据和表格,因而计算工作量较小,对计算工具要求不高。FIR滤波器则一般没有现成的设计公式,窗函数法只给出窗函数的计算工式,但计算通带、阻带衰衰减仍无显示表达式。一般FIR滤波器设计只有计算机程序可资利用,因而要借助于计算机。
6. IIR滤波器主要是设计规格化的、频率特性为分段常数的标准低通、高通、带通、带阻、全通滤波器,而FIR滤波器则要灵活得多,例如频率抽样设计法,可适应各种幅度特性的要求,因而FIR滤波器则要灵活得多,例如频率器可设计出理想正交变换器、理想微分器、线性调频器等各种网络,适应性较广。而且,目前已有许多FIR滤波器的计算机程序可供使用。
什么叫定点数?
计算机中采用的一种数的表示方法。参与运算的数的小数点位置固定不变。
什么叫滤波器的零点极点?
滤波器可以看成是一个信号处理的系统,其输入输出之间存在一定的关系,这种关系无论在时域还是频域都可以用数学表达式来表示.而这数学表达式又是分子分母都是多项式的表达式(称为传输函数),这样满足使传输函数的分子为零的是零点,满足使传输函数分母为零的就是其极点.
iir滤波器的种类:很多啊,直接一型,直接二型,级联型,并联型。
对于matlab的fdatool工具中二阶节默认结构为:
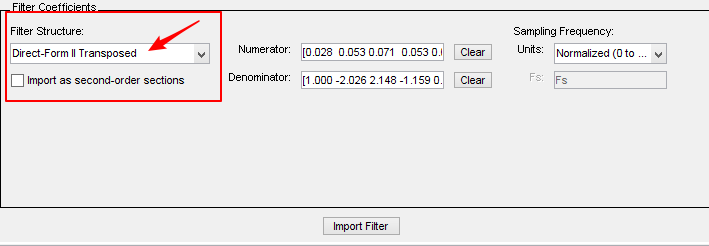
对于这个结构用图表示为:
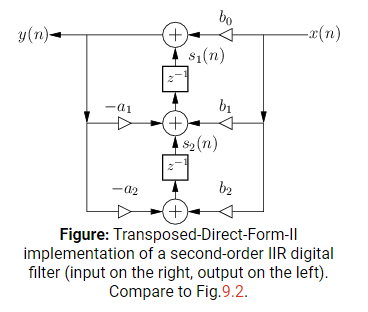
差分方程表示为:
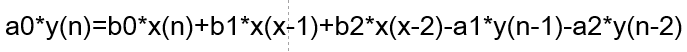
零极点表示为:零点就是差分方程的前面三项,极点就是后面两项。用FPGA实现主要就是实现滤波器的差分方程。

流程:
任务要求:
16阶二阶级联IIR数字滤波器设计,16bit有符号整数连续输入,采样率80khz,通带频率1k-8khz。系数为16bit有符号整数。
1.系数产生:通过matlab中的fdatool软件生成所需系数。(当然可以用各种函数生成,太难工科生表示要阵亡了,还是默默用fdatooll吧)
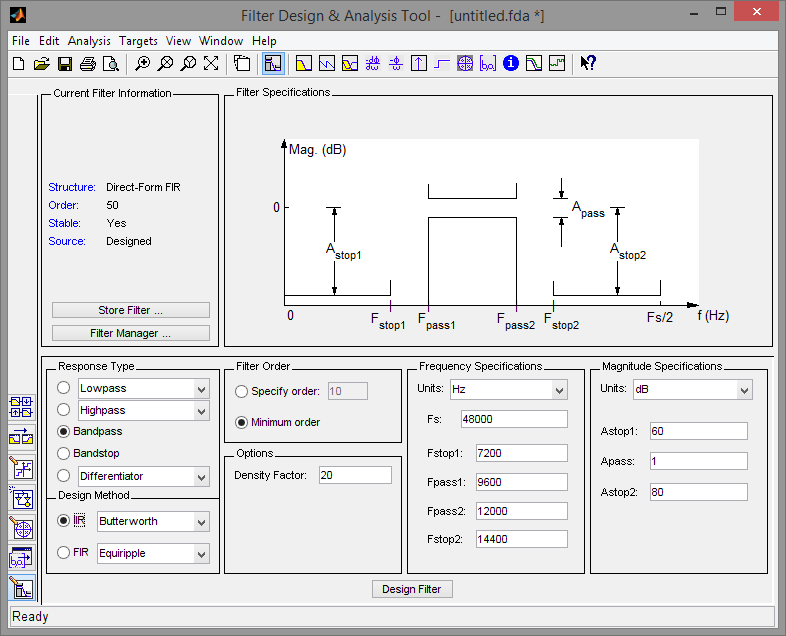
把需求放入fdatool中:生成的架构就是直接二型二阶节结构。
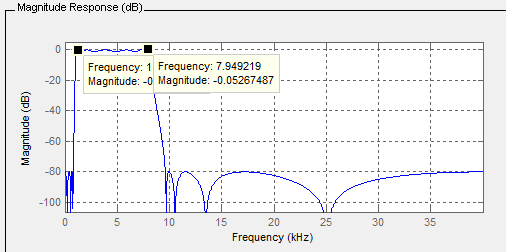
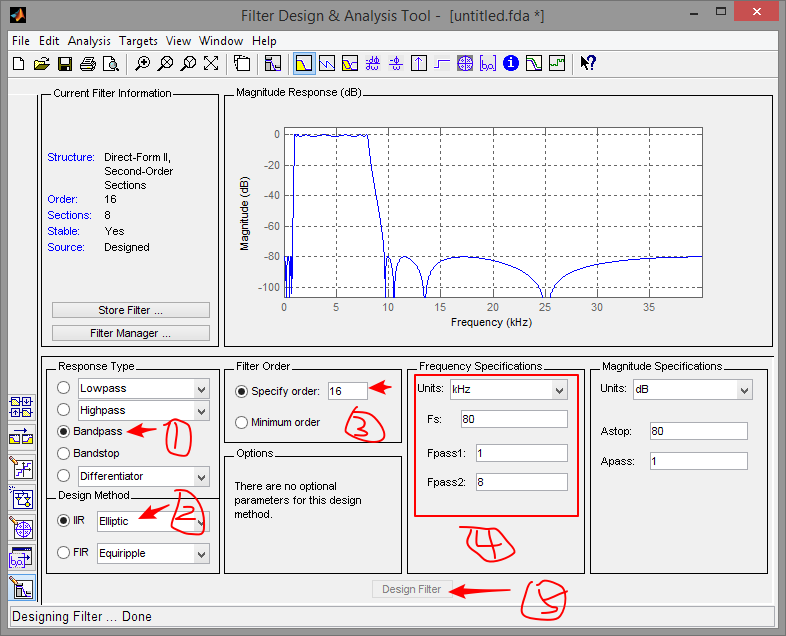
零极点图:
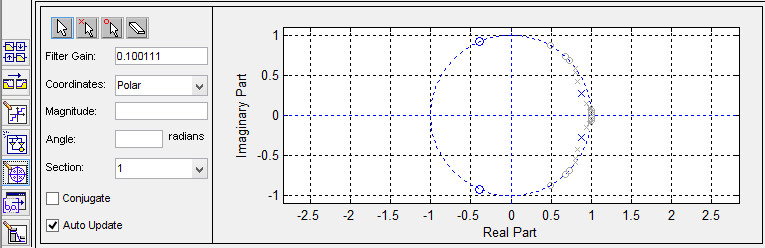
未量化的系数:
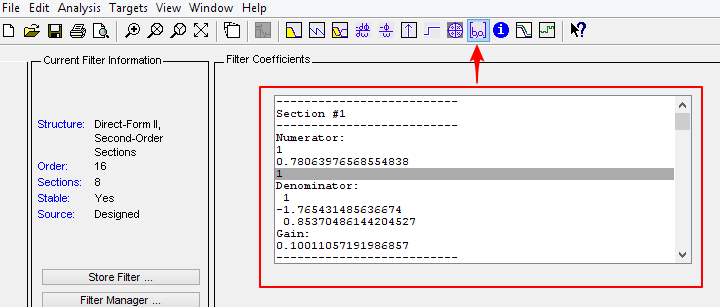
未量化的系数导出:生成一个c文件。
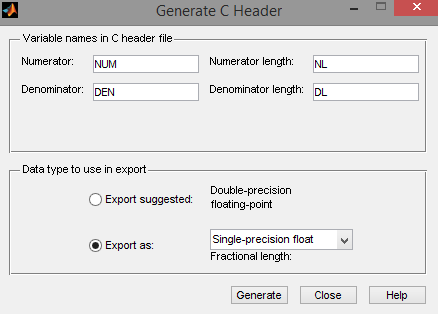
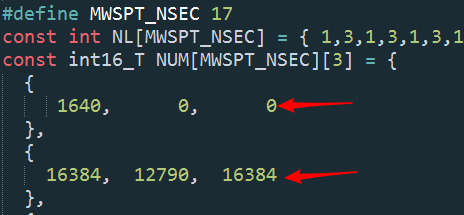
那么问题来了,这个c文件中的内容是啥子意思呢,一开始我也是一脸懵逼,而且网上的资料少之又少,文件如下所示,含义已注释:
1 /* 2 * Filter Coefficients (C Source) generated by the Filter Design and Analysis Tool 3 * 4 * Generated by MATLAB(R) 7.8 and the Signal Processing Toolbox 6.11. 5 * 6 * Generated on: 22-Sep-2017 20:23:35 7 * 8 */ 9 10 /* 11 * Discrete-Time IIR Filter (real) 12 * ------------------------------- 13 * Filter Structure : Direct-Form II, Second-Order Sections 14 * Number of Sections : 8 15 * Stable : Yes 16 * Linear Phase : No 17 */ 18 19 /* General type conversion for MATLAB generated C-code */ 20 #include "tmwtypes.h" 21 /* 22 * Expected path to tmwtypes.h 23 * D:workfileMatlab2009externinclude mwtypes.h 24 */ 25 /* 26 * Warning - Filter coefficients were truncated to fit specified data type. 27 * The resulting response may not match generated theoretical response. 28 * Use the Filter Design & Analysis Tool to design accurate 29 * single-precision filter coefficients. 30 */ 31 #define MWSPT_NSEC 17 32 const int NL[MWSPT_NSEC] = { 1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1 }; 33 //上面1313的玩意表示下面这个数组哪个项有效,1则表示第一项有效,3表示都有效; 34 const real32_T NUM[MWSPT_NSEC][3] = { 35 { 36 0.1001105756, 0, 0 //第一个二阶节的增益; 37 }, 38 { 39 1, 0.7806397676, 1 //第一个二阶节的零点;b0,b1,b2; 40 }, 41 { 42 0.1001105756, 0, 0 //第二个二阶节的增益; 43 }, 44 { 45 1, -1.999714136, 1 //第二个二阶节的零点;b0,b1,b2; 46 }, 47 { 48 0.3725369573, 0, 0 //以下就是类似的了; 49 }, 50 { 51 1, -0.9795594215, 1 52 }, 53 { 54 0.3725369573, 0, 0 55 }, 56 { 57 1, -1.99809742, 1 58 }, 59 { 60 0.6452683806, 0, 0 61 }, 62 { 63 1, -1.352879047, 1 64 }, 65 { 66 0.6452683806, 0, 0 67 }, 68 { 69 1, -1.996625185, 1 70 }, 71 { 72 0.7896357179, 0, 0 73 }, 74 { 75 1, -1.448690891, 1 76 }, 77 { 78 0.7896357179, 0, 0 79 }, 80 { 81 1, -1.995926261, 1 82 }, 83 { 84 1, 0, 0 //总的增益为1,上面8个分增益相乘最终为1; 85 } 86 }; 87 const int DL[MWSPT_NSEC] = { 1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1 }; 88 const real32_T DEN[MWSPT_NSEC][3] = { 89 { 90 1, 0, 0 //忽略项; 91 }, 92 { 93 1, -1.765431523, 0.8537048697 //第一个二阶节的极点;a0,a1,a2; 94 }, 95 { 96 1, 0, 0 97 }, 98 { 99 1, -1.893844962, 0.919323802 //以下类似; 100 }, 101 { 102 1, 0, 0 103 }, 104 { 105 1, -1.666594863, 0.877212882 106 }, 107 { 108 1, 0, 0 109 }, 110 { 111 1, -1.959967136, 0.9707458019 112 }, 113 { 114 1, 0, 0 115 }, 116 { 117 1, -1.614711642, 0.9346644878 118 }, 119 { 120 1, 0, 0 121 }, 122 { 123 1, -1.982463837, 0.9896451831 124 }, 125 { 126 1, 0, 0 127 }, 128 { 129 1, -1.603200555, 0.9806866646 130 }, 131 { 132 1, 0, 0 133 }, 134 { 135 1, -1.991223216, 0.9973948002 136 }, 137 { 138 1, 0, 0 139 } 140 };
系数量化选项:系数量化你可以自己量化也可以让软件量化,不过它量化出来的数据零点并不是乘完增益后再进行量化的。最好还是乘完增益后再量化,所以还是自己用excel慢慢量化吧,眼泪掉下来。
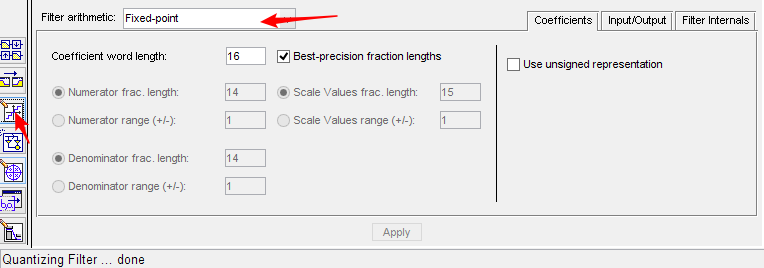
未量化excel表:
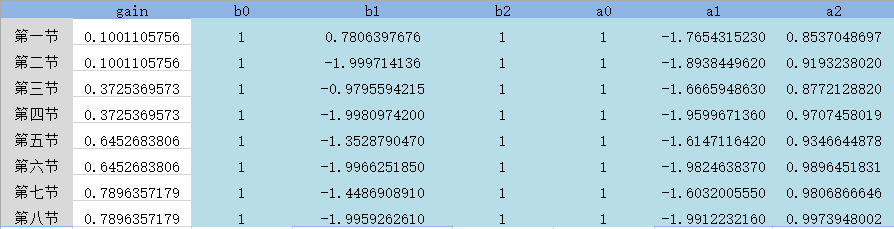
excel中计算单元格方便到不行:零点乘完增益放大16384;极点直接放大16384;下图gain请无视。
新的b0=b0*gain1*16384;新的a0=a0*16384;放大16384倍方便FPGA实现除法截位。
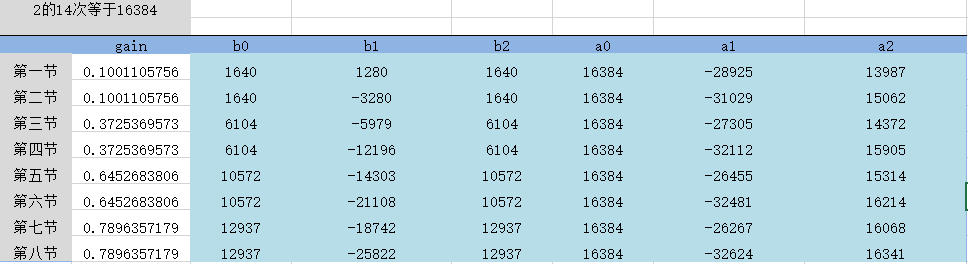
2.编码实现:
先看一下16阶iir滤波器架构:级联8个二阶节。
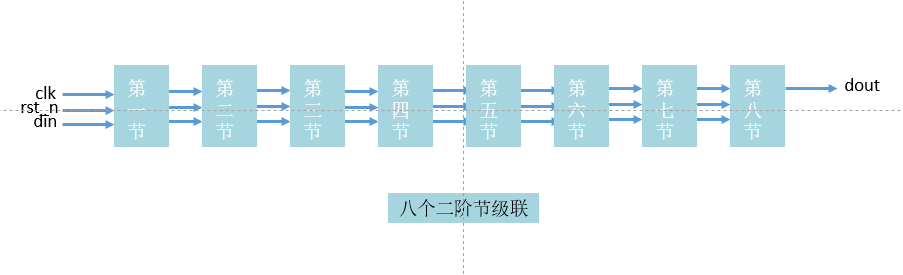
一个二阶节:
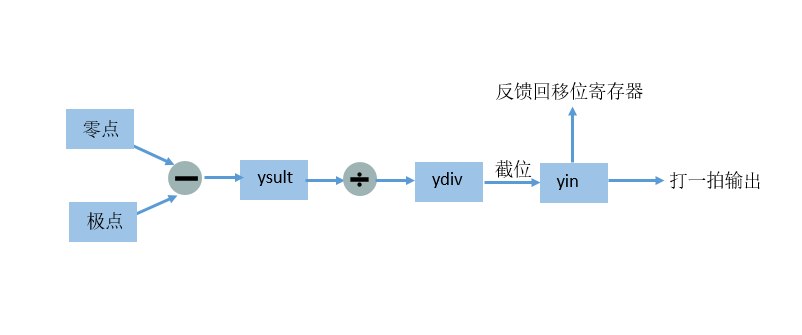
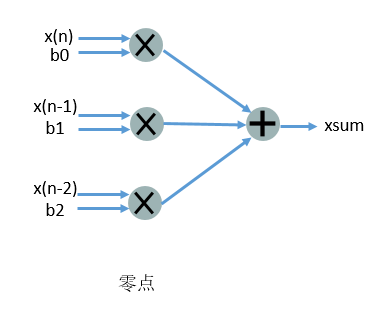
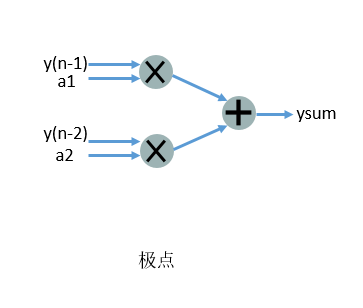
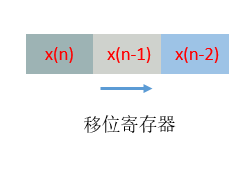
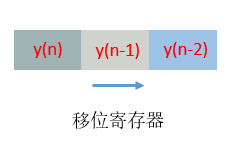
现在就可以编码实现它了,这是第一版代码,尚未优化,仿真ok,不要逻辑综合,会占用成吨的资源。
由于技术垃圾,不做十分精确输出位控制,输出都为16bit数据。
两个n位的加法结果需要n+1位;两个n位的乘法结果需要2n位。
matalb生成modelsim仿真文件向量:
生成1500hz,采样80khz波形向量文件。生成其他hz的波形文件类似。
1 f1=1500; %频率1500hz; 2 Fs=80000; %采样80khz; 3 N=16; %16bit量化; 4 t=0:1/Fs:0.01; %采样时长0.01; 5 c2=2*pi*f1*t; 6 s2=sin(c2); %正弦波产生; 7 s2=s2/max(abs(s2)); 8 Q_s=round(s2*(2^(N-1)-1)); 9 plot(t,s2,'r*-'); %画图; 10 11 fid=fopen('D:datadata_1500data_1500.txt','w'); %采样点保存为10进制; 12 fprintf(fid,'%8d ',s2); 13 fprintf(fid,';'); 14 fclose(fid); 15 16 fid=fopen('D:datadata_1500data_1500_B.txt','w'); %采样点保存为2进制; 17 for i=1:length(Q_s) 18 B_s=dec2bin(Q_s(i)+(Q_s(i)<0)*2^N,N) 19 for j=1:N 20 if B_s(j)=='1' 21 tb=1; 22 else 23 tb=0; 24 end 25 fprintf(fid,'%d',tb); 26 end 27 fprintf(fid,' '); 28 end 29 fprintf(fid,';'); 30 fclose(fid);
仿真测试:
对600hz正弦波滤波结果:600hz波形被滤除。
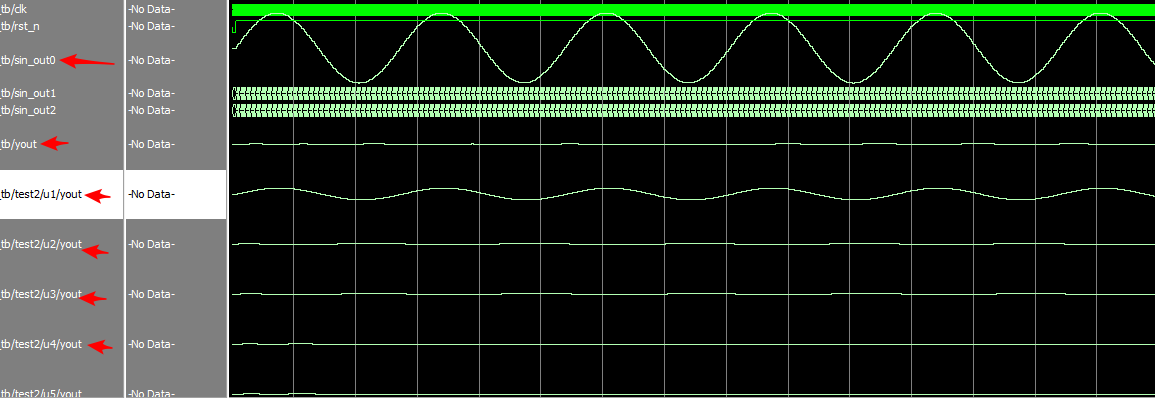
对5000hz正弦波滤波结果:5000hz波形通过。
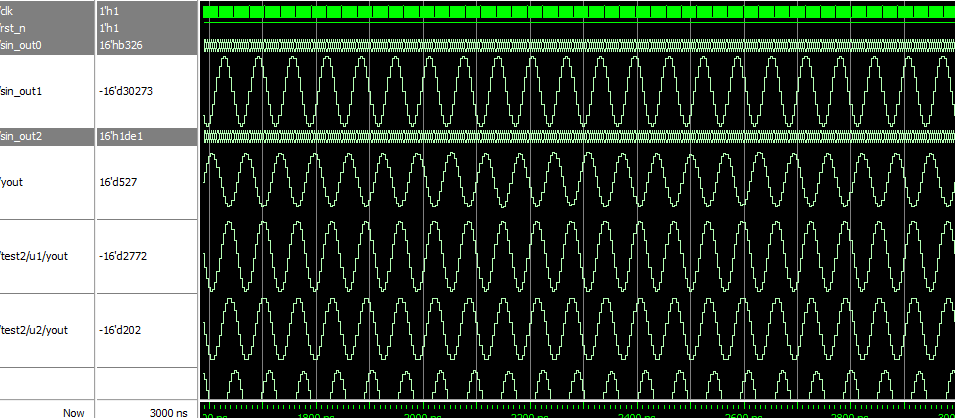
对9000hz波形滤波结果:开始有点点迷之振荡,基本滤除9000hz的波。
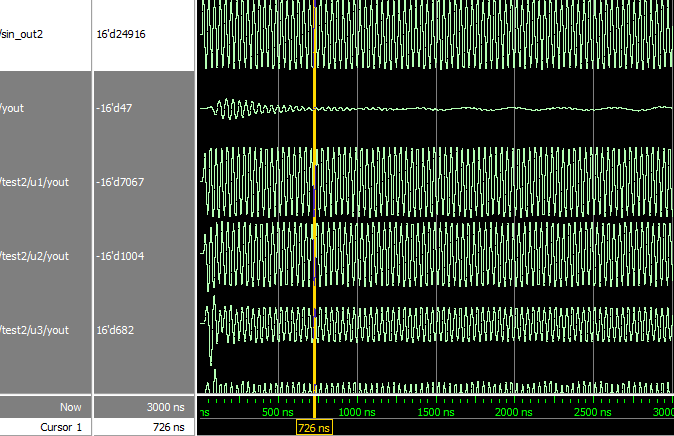
最开始的结果经过多久出来到out?(特么上次面试还问这个了,十脸懵逼,根本没注意这啊。。。emmm很气)
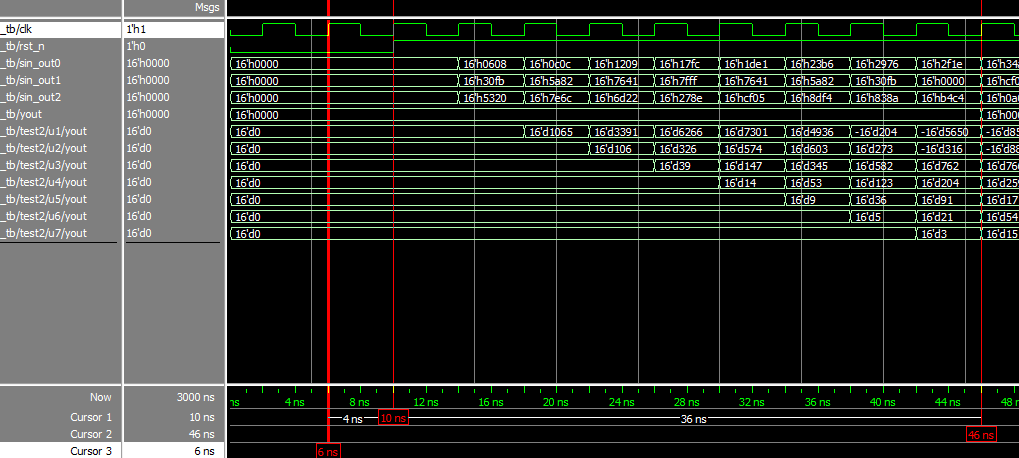
可以看到是复位拉高后的9个时钟周期后yout数据产生,因为流水线啊,emmm。
初版代码综合上板子:通过rom输出5khz的数据。
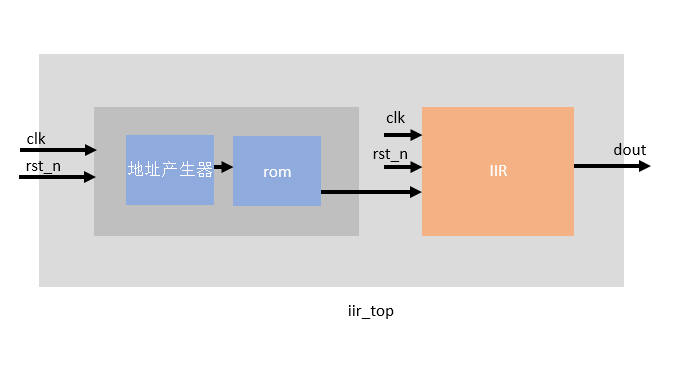
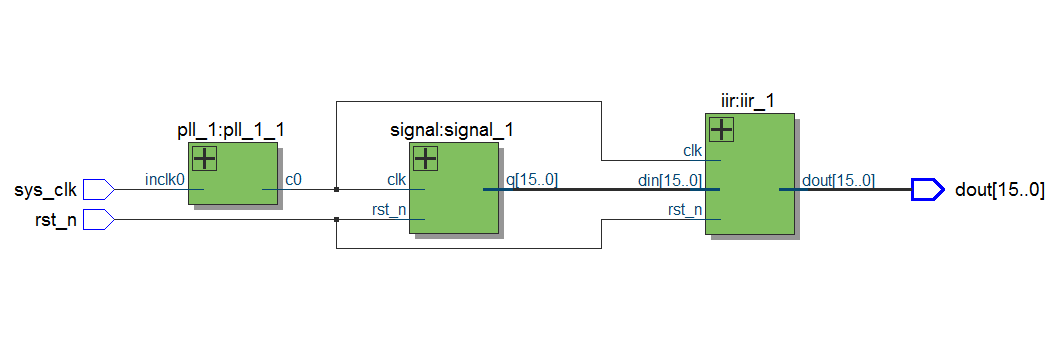
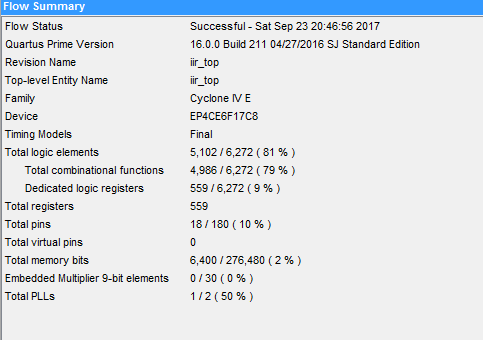
所以优化很重要,这是未优化版本。
signaltapII抓下波:
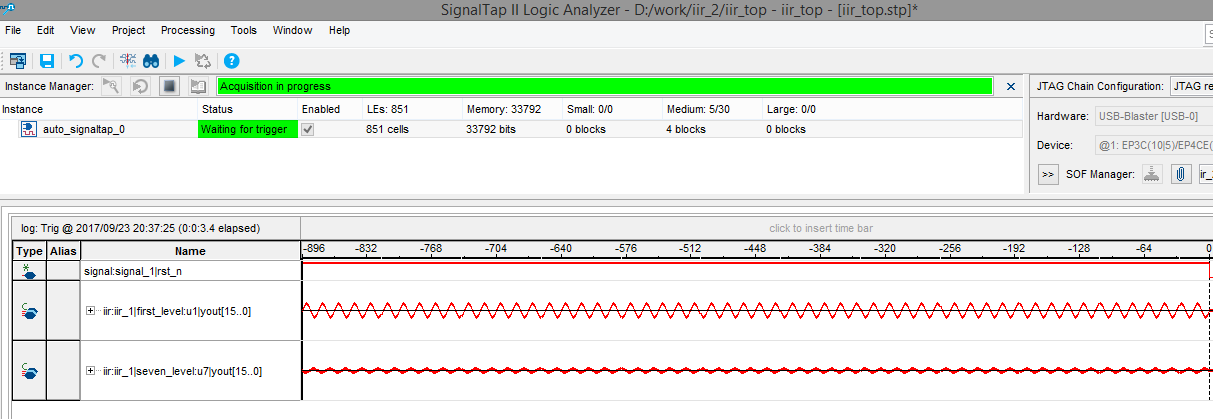
优化版以及未优化版比较:只包含iir部分,不含pll以及rom。系统时钟跟采样时钟一样,80khz。
未优化版:直接采用*(乘)的方式。
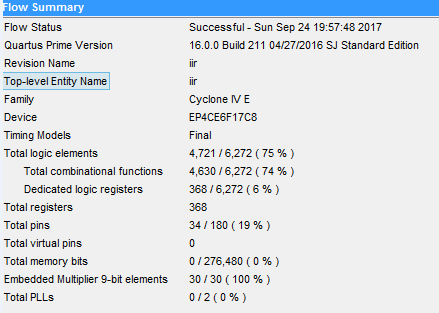
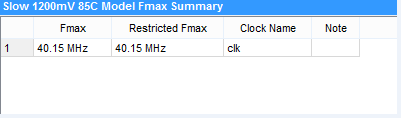
优化版:采用内置乘法器,以及采用移位相加的方法。资源少的可怜啊,一共才30个9bit乘法器。。。。,若再增加乘法器,le使用量又会往上涨。未来优化方向:提高时钟频率,复用乘法器。
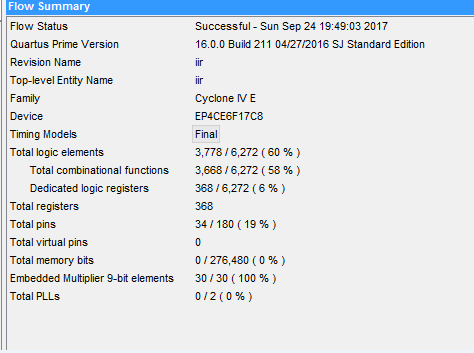
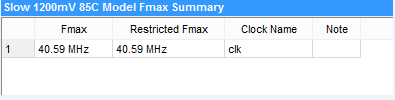
其他:
怎么优雅的分解系数用来移位相加:
直接写了个c程序,来看看效果:
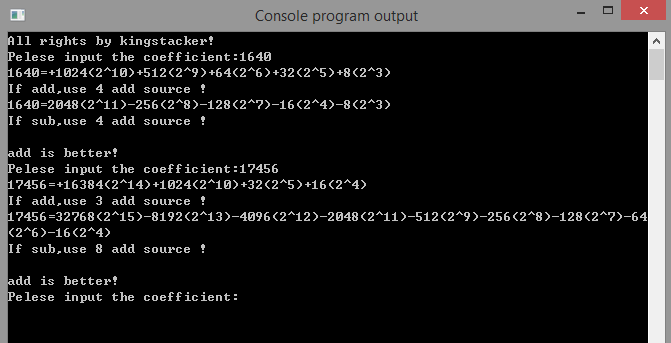
c源代码:看看就好啦,很久没写c,完全没有代码style了emmm。
1 #include <stdio.h> 2 #include <math.h> 3 int main(void) 4 { 5 int coefficient; 6 int sum; 7 int sum1; 8 int mul; 9 int mul1; 10 int j; 11 int i; 12 int k=0; 13 int m; 14 int n=0; 15 int cha; 16 printf("All rights by kingstacker! "); 17 begin: 18 printf("Pelese input the coefficient:"); 19 scanf("%d",&coefficient); 20 printf("%d=",coefficient); 21 sum = coefficient; 22 sum1 = coefficient; 23 for (m=15;m>=0;m--) //add; 24 { 25 mul1=pow(2,m); 26 if (sum1 >= mul1) 27 { 28 sum1 = sum1 -mul1; 29 n=n+1; 30 printf("+%d(2^%d)",mul1,m ); 31 32 } 33 34 } 35 printf(" If add,use %d add source ! ",n-1 ); 36 //sub; 37 for (j=0;j<=15;j++) 38 { 39 mul=pow(2,j); 40 if (mul >= sum) 41 { 42 goto this; 43 } 44 } 45 this: 46 cha = mul - sum; 47 printf("%d=%d(2^%d)",sum,mul,j ); 48 for (i=j;i>=0;i--) 49 { 50 mul1 = pow(2,i); 51 if (cha >= mul1) 52 { 53 cha = cha - mul1; 54 k=k+1; 55 printf("-%d(2^%d)",mul1,i ); 56 } 57 } 58 printf(" If sub,use %d add source ! ",k ); 59 //result; 60 if((n-1) <= k) 61 { 62 printf(" add is better! "); 63 } 64 else 65 { 66 printf(" sub is better! "); 67 } 68 k=0; 69 n=0; 70 goto begin; 71 printf("Thanks for you use!bye! "); 72 73 }
以上。