Style:Mac
Series:Java
Since:2018-09-10
End:2018-09-10
Total Hours:1
Degree Of Diffculty:5
Degree Of Mastery:5
Practical Level:5
Desired Goal:5
Archieve Goal:3
Gerneral Evaluation:3
Writer:kingdelee
Related Links:
http://www.cnblogs.com/kingdelee/
https://www.jianshu.com/p/65c90aa1236d
https://www.cnblogs.com/zhangbaochong/p/5164994.html
http://www.cnblogs.com/skywang12345/p/3577479.html
https://blog.csdn.net/qq_25806863/article/details/74755131
https://blog.csdn.net/skyroben/article/details/72824146
1.在put的时候,当节点数>=7时,会执行进化树结构,调用treeifyBin(tab, hash)
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
logger.info("p.next为空,为其创建新的节点,p.next.hash:" + hash + ", p.next.value:" + value);
p.next = newNode(hash, key, value, null); // 将当前的节点的下一个节点指向新创建的节点
if (binCount >= TREEIFY_THRESHOLD - 1) // 只有>=7次迭代才会执行进化树结构
{
logger.info("binCount >= (TREEIFY_THRESHOLD - 1), binCount:" + binCount + ", (TREEIFY_THRESHOLD - 1):" + (TREEIFY_THRESHOLD - 1));
treeifyBin(tab, hash);
}
logger.info("跳出循环");
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))){
logger.info("同一个对象");
break;
}
logger.info("p.next有值, p.next.hash:" + p.next.hash + ",p.next.value:" + p.next.value + ", 把当前p指针指向p.next");
p = e;
}
2. 每次在同坑位的节点>=7的情况下,但凡put节点进来都会进行一次扩容
所以,在容量小于64时,在当同坑位的节点>=7,每递增一个节点,进行一次扩容
当容量大于64时,进化树结构。
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
logger.info("n = tab.length:" + tab.length);
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) //小于最小默认树结构容量64时进行扩容
{
logger.info("小于树最小容量阀值64,进行扩容");
resize();
}
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
3.说说树
为毛要用树这种结构?
原理引用:1.有序数组虽然查询快插入慢,而链表插入快但是查询慢;
而树的查找效率如下,层数是遍历次数,时间复杂度 O(logN)
以下源自《Java数据结构和算法(第二版)》
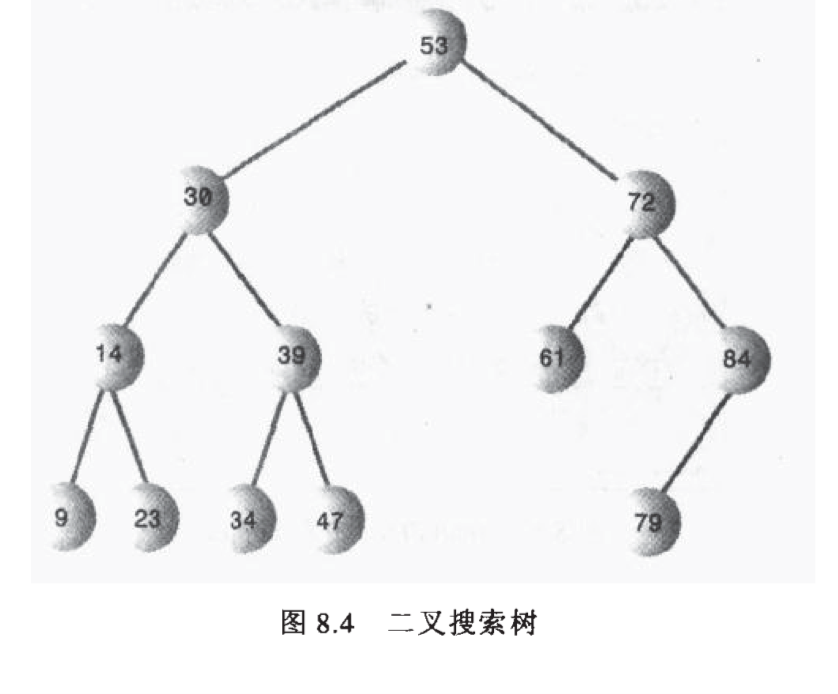




红黑树


必须满足4个规则:
1.每一个节点不是红色就是黑色
2.根总是黑色
3.若节点时红色,则其子节点一定是黑
4.从根到叶节点或非空子节点的每条路径,必须包含相同数量的黑色节点
5.每个叶节点(NIL,即正常情况下的最后一个节点的1个或2个隐式节点)都是黑的
3.AVL
平衡检测
高度(height):从根节点(root)开始到某一个叶子节点(leaf)的最长路径(path)上结点的个数
平衡因子(balanced factor):某个结点的平衡因子等于该节点的左孩子的高度减去右孩子的高度
根据平衡树的定义,计算得到的平衡因为会出现两种情况:
- 如果平衡因子是
0,1,-1这三个数的话,可以认定该节点是符合平衡树的定义的; - 否则,该结点不平衡,需要重新平衡;
重平衡
如果发现了某个不平衡的结点,那么就需要对该结点进行重平衡。实现重平衡的方法,是对该节点的子树进行旋转(rotation)。
把需要重新平衡的结点叫做α,由于任意两个结点最多只有两个儿子,因此高度不平衡时,α结点的两颗子树的高度相差2.容易看出,这种不平衡可能出现在下面4中情况中:
1.对α的左儿子的左子树进行一次插入
2.对α的左儿子的右子树进行一次插入
3.对α的右儿子的左子树进行一次插入
4.对α的右儿子的右子树进行一次插入
举例:
1.最初的AVL
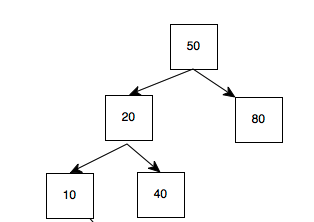
50先插入,50为根;再插入的20比50小,故应插入50左下,作为50的左子树;再插入的80比50大,故应插入50的右下,作为50的右子树;
插入10,比50小,左下,比20小,左下;插入40,比50小,左下,比20大,右下;
故,这图为,50为根,50的左子树是以20为根的子树(20,10,40....),50的右子树以80为根的子树
50的左子树长度是20->10,即2;右子树长度为1;2-1=1,符合平衡树的差值;这是一个AVL树
此时,倘若只要左子树再增加一个长度(即插入诸如2,12,30,45等)
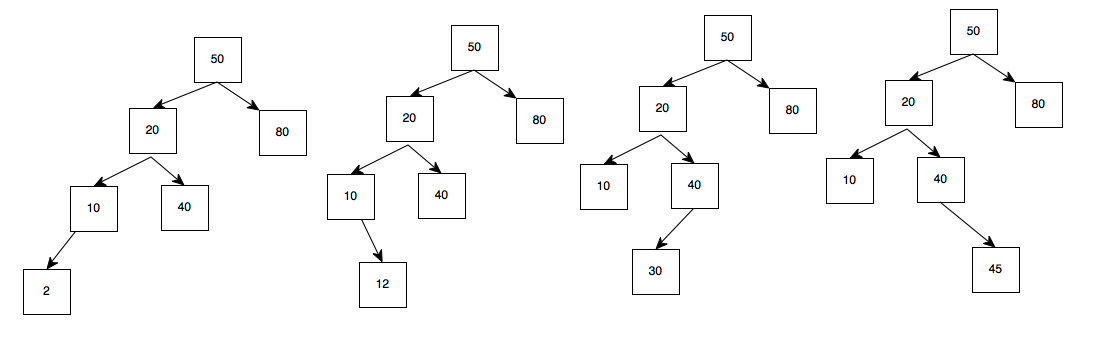
50的左子树的长度变为3,而右子树的长度为1,差值为2而不是小于等于1,此时,不符合AVL树的要求。
故在AVL的规范下,需要对此时的非AVL做调整形成AVL树
对其中(添加2或12)此种,左子树(20->10>2或20->40->30)比右子树(80)的路径>1,且是在最后一层(10, 40)的左边,称为:LL左左
对其中(添加30或45)此种,左子树(20->40>30或20->40->45)比右子树(80)的路径>1,且是在最后一层(10, 40)的右边,称为:LL左右
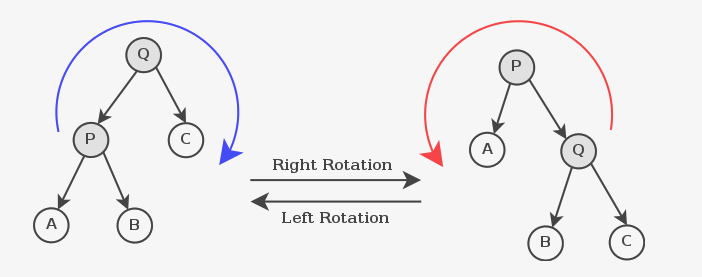
对于LL左左的旋转操作:
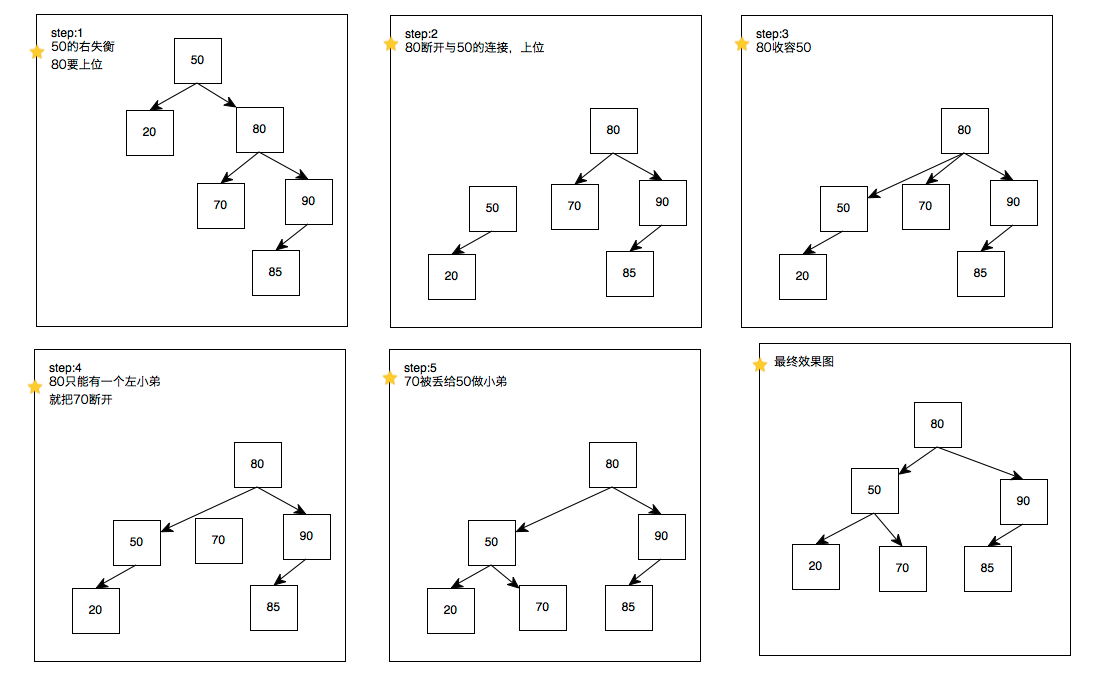
左旋:操作如下图【最好用谁强大谁上位来理解,否则用旋转理解,谁旋谁死;见过有硬硬解释旋转的,还用通过逆顺时针来解释的,勉强多看几次是能看懂但不好理解会忘;绝无仅有,申请专利,将xx旋转更名为Lee上位:)】
白话左旋就是,50根失去左平衡,受不了左边20的压力就断开与左20的连接;20成功上位,但是不能不管曾经的老大根,所以,把旧老大作为自己的右小弟(右子树);只能有一个右小弟呐,新老大20认为旧老大50好歹也做过老大经验丰富,就把自己的小弟40丢给旧老大50左他的小弟。完。左旋一点都不好理解,应理解为哪边失衡(变强大),哪边就要上位了。
所以ll左左如下,左左是其他变形的基础,其他都是变形的理解都是建立在这个东西之上的。
------------------------------------
对于LR左右:
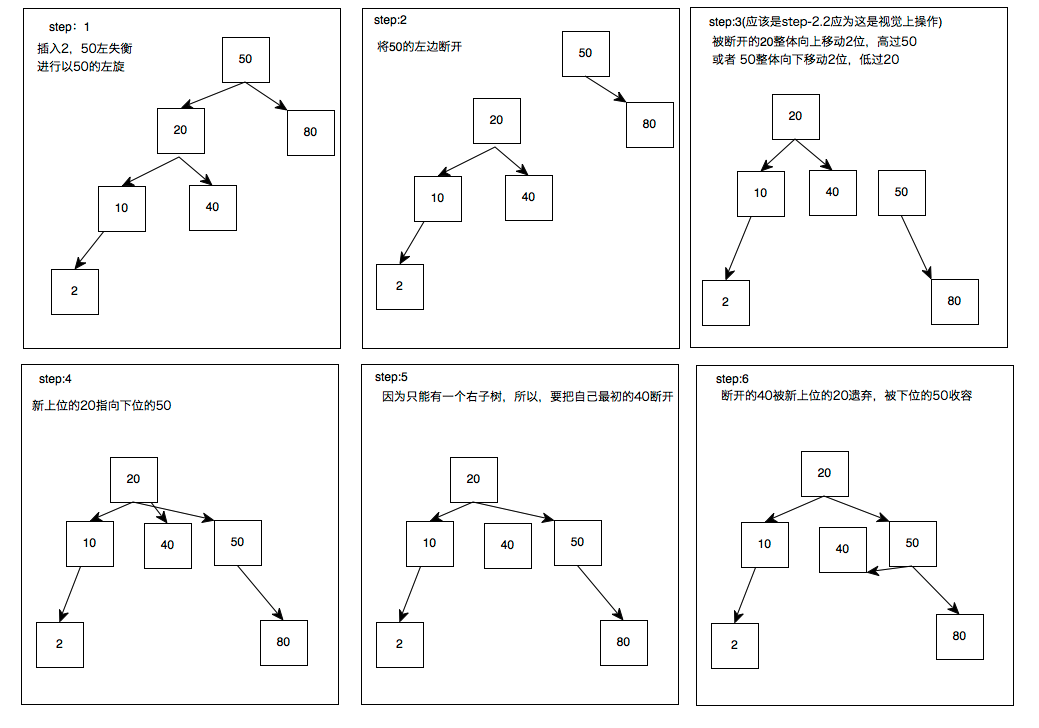
我们采取和之前上位一样的操作
50的左子树失衡,断开与20的连接;20上位,右边重连50,把40丢给50持有。
发现仍失衡
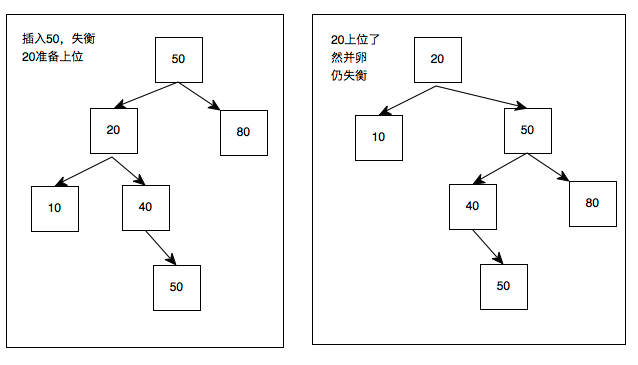
为毛在10底下的新节点就行,为在40底下的新节点就不行?啊咧,仅有这样的区别的话,想办法形成和之前的最初的左左的图一样不就可以了吗
于是:
20上位行不通,40上位试一试。
第一次上位:验算中发现20太弱尝试做老大是失败的(这一步不需要实操),20的小弟40要上位;20断开与50的连接,40上位20;40与50产生连接成为新的小王;20被40收容做小弟。可是仍没平衡呐,但是出现LL形状了,胜利就在眼前,40可以采取LL的方式继续上位
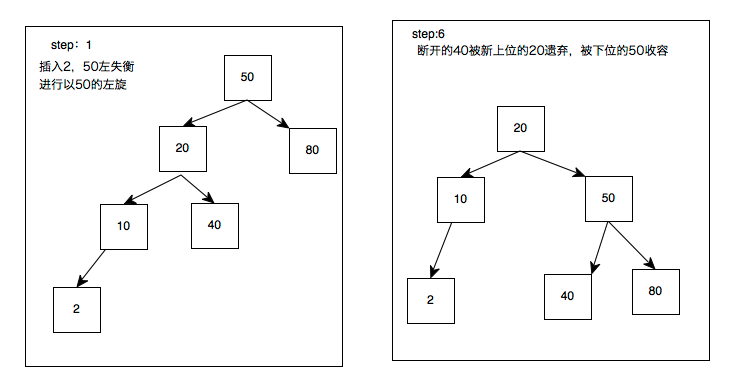
第二次上位:和LL一样,40断开与50的连接上位,50成为40的小弟;40把自己的小弟45丢给前老大50收容,AVL了
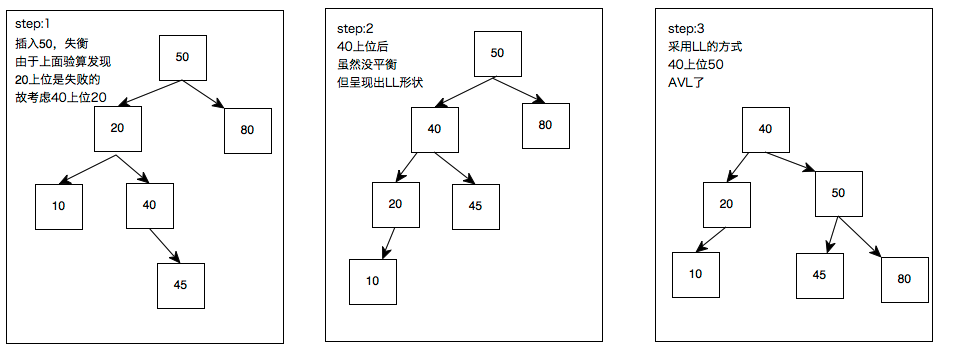
以上解决了LL和LR两种图形
结论是:
1.当发现新加入的节点造成根出现左子树失衡,且新加入的节点是在叶节点(最后一层)的左节点上,即为LL;老二上位1次即可
2.当发现新加入的节点造成根出现左子树失衡,且新加入的节点是在叶节点(最后一层)的右节点上,即为LR;老三上位2次即可
----------------------------------------------------
如果AVL是这样子的,插入以下新的节点都会导致AVL失衡,和上面很像了
同理,1、2是RL,3、4是RR
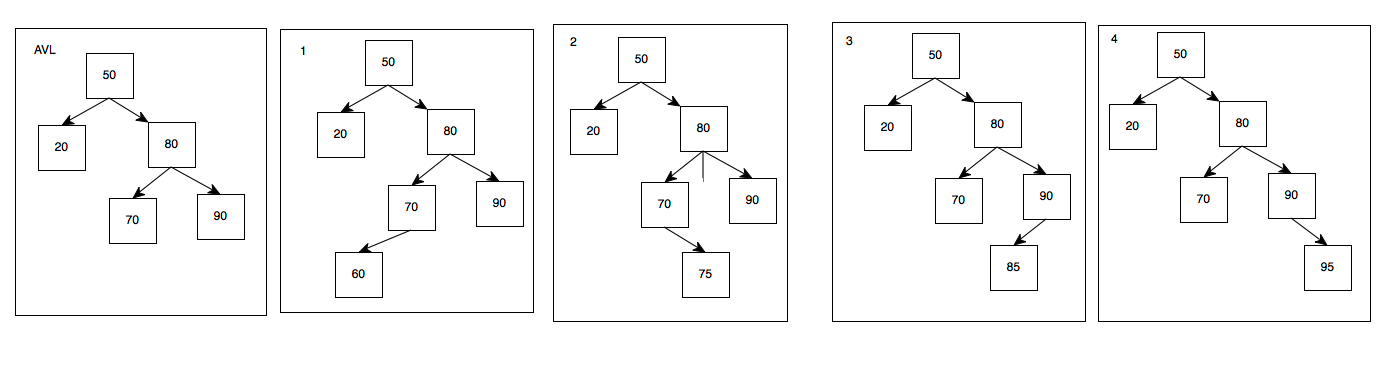
先看3、4的RR,这个是基础
RL呢
跟之前是类似的
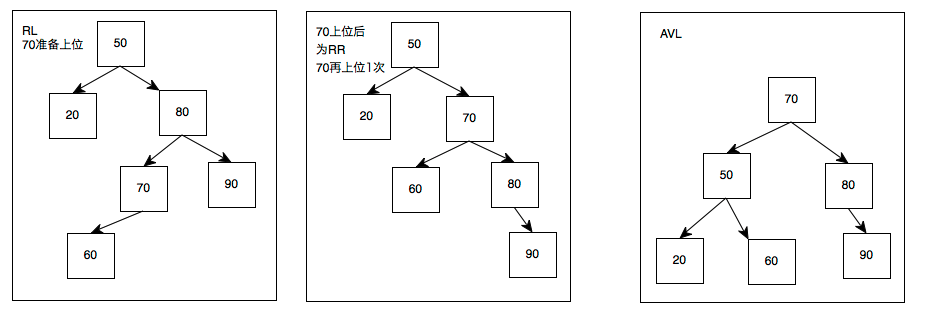
可是,以上仍然不够严谨
因为
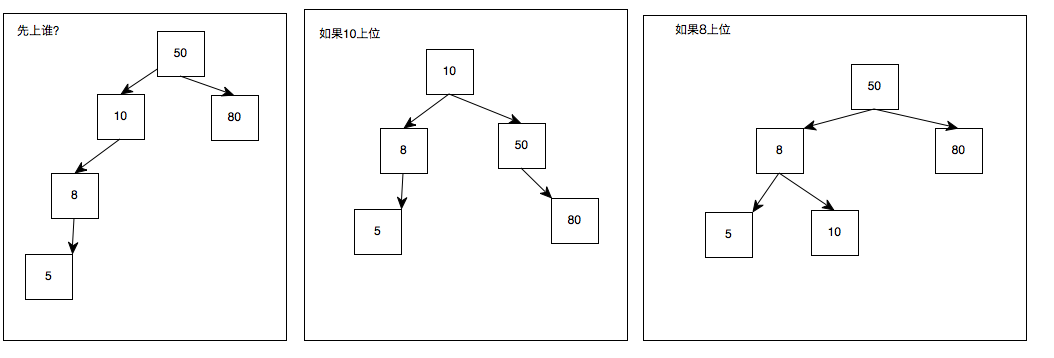
两种都能够保持AVL,但是哪种才是正确的呢
结论是:8上位。
直观理由:1.这样变动更少,2.更安全.3.最近原则
问题来了:没法总是看图,如何用代码表示呢
引用了所谓的平衡因子c
重新看一下LL:
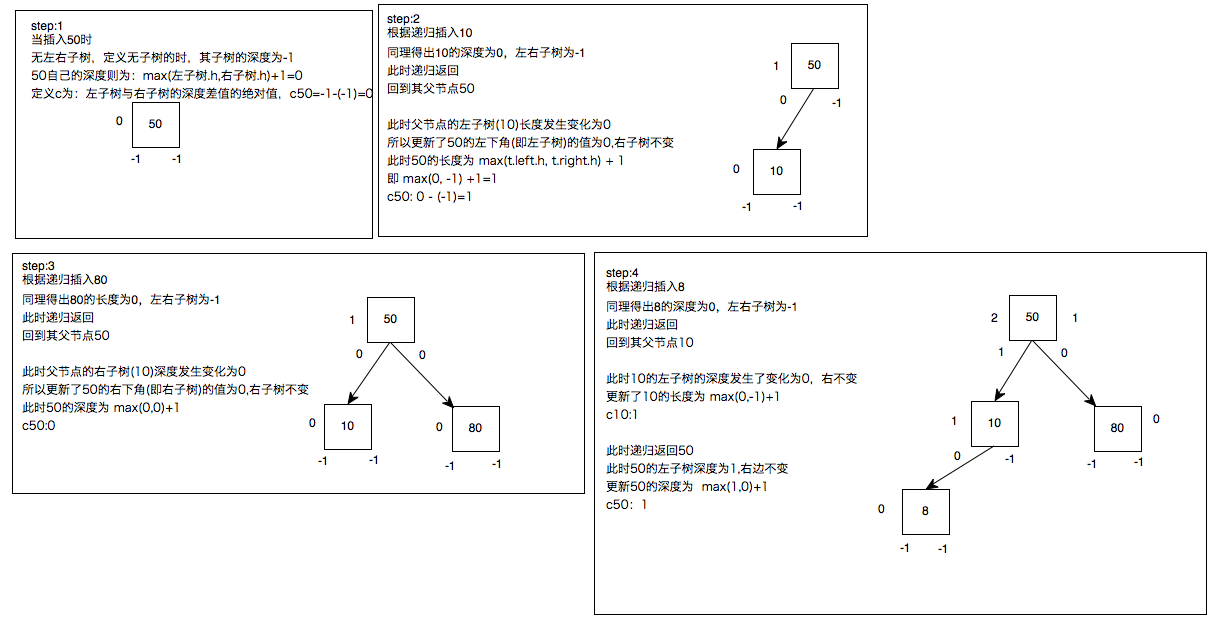
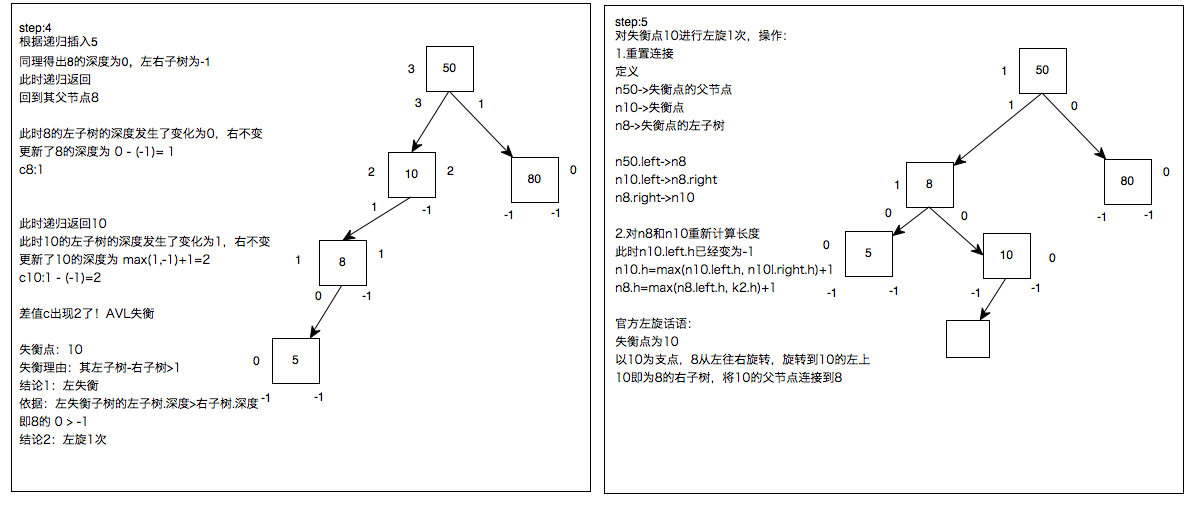
看一下LR
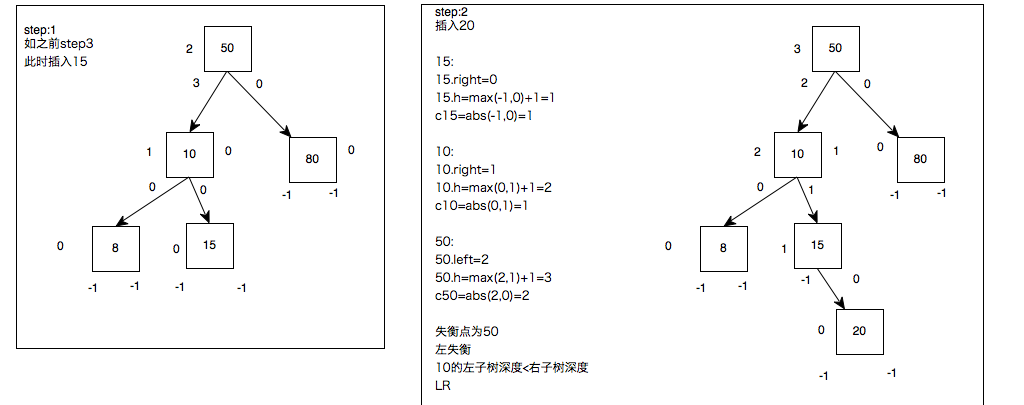
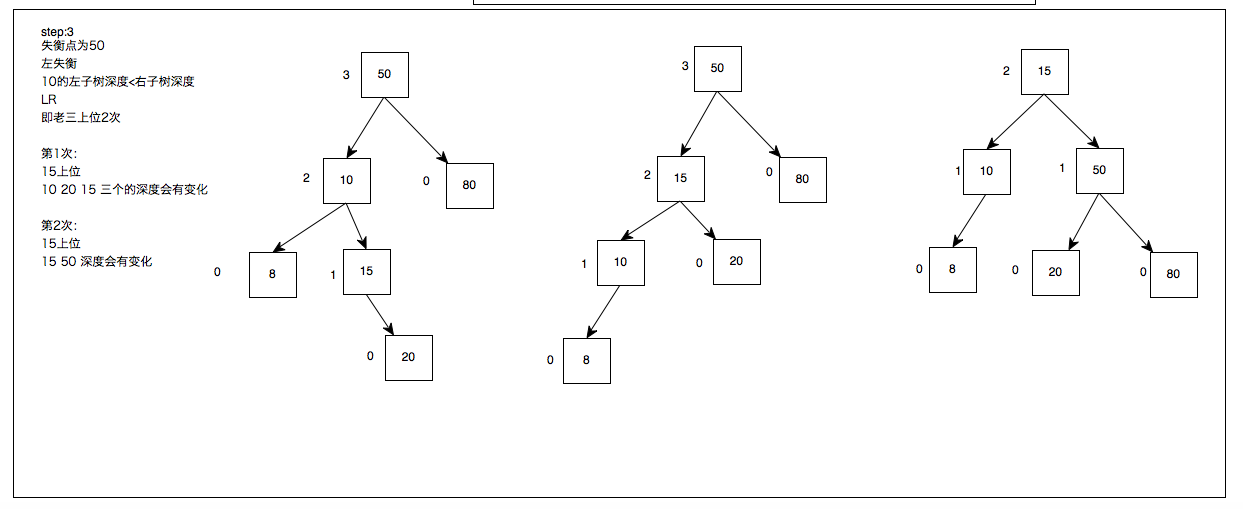
RR RL依据之前没给出深度值的加上深度值就可以了