最大连续子数组和(简单一维dp)

最大连续子数组和(简单一维dp)

一、题目：

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n

例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

-- 引用自《百度百科》

二、分析

经典的简单一维dp题目，设另一数组b，b[i]表示以a[i]为结尾的最大和。最大连续子数和sum值为b数组中最大值。又因判断a[i]时，前i-1个数无用，可将b结合进a数组达到空间最优。整理如下:

$$a[i]=max(a[i],a[i]+a[i-1])$$

$$sum=max(a[1],a[2]...,a[n])$$

三、代码

我用myeclipse编辑java程序，代码如下：

public class Main {
      public static int mainsum(int[] a,int n){
    	  int sum = 0;
    	  if(a[0] > 0)
    		  sum = a[0];
    	  for(int i = 1; i < n; i++){
    		  a[i] = Math.max( a[i], a[i] + a[i-1]);
    	      if(sum < a[i])
    	    	  sum = a[i];
    	  }
    	  return sum;
      }
}

四、覆盖测试

我选用条件组合覆盖，根据程序绘制流程图如下：

因为每个判定均为单条件判定，当考虑i时，将会有((2×2)^n)种可能，所以无法考虑i值。那么，只需2×2种情况即可条件组合覆盖。四种情况，一种特殊情况，测试样例及结果如下：

情况	用例	结果
a[i]<=a[i]+a[i-1]&&sum<=a[i]	1,2,3,4,5,6	21
a[i]>a[i]+a[i-1]&&sum>a[i]	1,-2,-3,-4,-5,-6	1
a[i]>a[i]+a[i-1]&&sum<=a[i]	1,-2,3,-4,5,-6	5
a[i]<=a[i]+a[i-1]&&sum>a[i]	10,-17,5,4,-7,6	10
特殊情况（全部小于0）	-1,-2,-3,-4,-5,-6	0

测试代码如下：

public class MainTest {

	@Test
	public void testMainsum1() {
		int[] a = new int[]{1,2,3,4,5,6};
		int sum = new Main().mainsum(a , 6);
		assertEquals(21 , sum );
	}
	
	@Test
	public void testMainsum2() {
		int[] a = new int[]{1,-2,-3,-4,-5,-6};
		int sum = new Main().mainsum(a , 6);
		assertEquals(1 , sum );
	}
	
	@Test
	public void testMainsum3() {
		int[] a = new int[]{1,-2,3,-4,5,-6};
		int sum = new Main().mainsum(a , 6);
		assertEquals(5 , sum );
	}
	
	@Test
	public void testMainsum4() {
		int[] a = new int[]{10,-17,5,4,-7,6};
		int sum = new Main().mainsum(a , 6);
		assertEquals(10 , sum );
	}
	
	@Test
	public void testMainsum5() {
		int[] a = new int[]{-1,-2,-3,-4,-5,-6};
		int sum = new Main().mainsum(a , 6);
		assertEquals(0 , sum );
	}
}

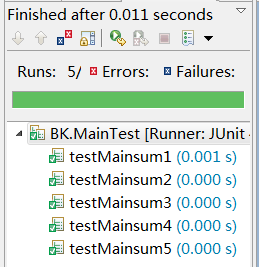
测试结果如下：

全部代码：代码地址