3.2 直线与方程

3.2.1 直线的点斜式方程
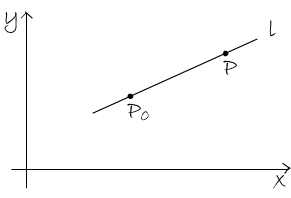
直线 (l) 经过点 (P_0(x_0,y_0))，且斜率为 (k)，设 (P(x,y)) 是直线 (l) 上不同于 (p_0) 的任意一点，因为 (l) 的斜率为 (k)，由斜率公式得

[k=frac{y-y_0}{x-x_0} ]

即

[y-y_0=k(x-x0) ]

如果直线 (l) 的斜率为 (k)，且与 (y) 轴的交点为 ((0,b))，代入直线的点斜式方程，得

[y-b=k(x-0)， ]

即
(y=kx+b ag{2})
我们把直线 (l) 与 (y) 轴交点为 ((0,b)) 的纵坐标 (b) 叫做直线 (l) 在 (y) 轴上的截距。方程 ((2)) 由直线的斜率 (k) 与它在 (y) 轴上的截距 (b) 确定，所以方程 ((2)) 叫做直线的斜截式方程，简称斜截式。

---

3.2.2直线的两点式方程
当 (x_1 eq x_2) 时， 所求直线的斜率 (k=frac{y_2-y_1}{x_2-x_1})，任取 (P_1)，(P_2) 中的一点，例如，取 (P_1(x_1,y_1))，由点斜式方程，得

[y-y_1=frac{y_2-y_1}{x_2-x_1}(x-x_1), ]

当 (y_2 eq y_1) 时，可写为

[frac{y-y_1}{y_2-y_1}=frac{x-x_1}{x_2-x_1} ]

这就是经过两点 (P_1(x_1,y_1))，(P_2(x_2,y_2))（其中(x_1 eq x_2)，(y_1 eq y_2)）的直线方程，我们把它叫做直线的两点式方程，简称两点式

---

3.2.3直线的一般式方程
任意一条直线 (l) ，在其上任取一点 (P_0(x_0,y_0))，当直线 (l) 的斜率为 (k) 时（引时直线的倾斜角 (a=90^o)），其方程为
(y-y_0=k(x-x_0) ag{1})
这是关于 (x，y) 的二元一次方程。
当直线 (l) 的斜率不存在，即直线 (l) 的倾斜角 (a=90^o) 时，直线的方程为
(x-x_0=0， ag{2})
方程 ((2))可以认为是关于 (x,y) 的二元一次方程，此时方程中的 (y) 的系数为 0.
方程 ((1)) 和方程 ((2)) 都是二元一次方程，因此平面上任意一条直线都可以用一个关于 (x，y) 的二元一次方程表示。
现在探讨问题：每一个关于 (x,y) 的二元一次方程都表示一条直线吗？
对于任意一个二元一次方程
(Ax+By+C=0 (A,B不同时为0), ag{3})
判断它是否表示一条直线，就看能否把它化成直线方程的某一种形式。
当 (B eq 0) 时，方程 ((3)) 可变形为
$$y=- frac{A}{B}x-frac{C}{B}$$
它表示过点 ((0，- frac{C}{B}))，斜率为 (-frac{A}{B}) 的直线
由上可知，关于 (x，y) 的二元一次方程，它都表示一条直线。
我们把关于 (x,y) 的二元一次方程
(Ax+By+C=0 (A，B不同时为0) ag{5})
叫做直线的一般式方程，简称一般式（general form）.
求直线的点斜式和一般式方程
例5 已知直线经过点 (A(6，-4))，斜率为 (-frac{4}{3})，求直线的点斜式和一般式方程。
解：经过点 (A(6，-4))，斜率等于 (-frac{4}{3})的点斜式方程是
$$y+4=- frac{4}{3}(x-6)$$
化成一般式，得
$$4x+3y-12=0$$

---

3.3.3 点到直线的距离
如下图，设 (A eq 0，B eq 0)，则直线 (l) 与 (x) 轴和 (y) 轴都相交，过点 (P_0) 分别作 (x) 轴和 (y) 轴的平行线，交直线 (l) 于 (R) 和 (S)，则直线 (P_0R) 的方程为 (y=y_0)，(R) 的坐标为 (left(- frac{By_0+C}{A}，y_0 ight))；直线 (P_0S) 的方程为 (x=x_0)，(S) 的坐标为 (left(x_0，- frac{Ax_0+C}{B} ight)) 。

于是有 $egin{aligned} left | P_0R ight |&=left |-{frac{By_0+C}{A}}-x_0 ight |= frac{left |Ax_0+By_0+C ight |}{left | A ight |}\ left | P_0S ight |&=left |- frac{Ax_0+C}{B}-y_0 ight |=frac{left |Ax_0+By_0+C ight |}{left | B ight |}\ left | RS ight |&=sqrt{{ left | P_0R ight |}^2+{left |P_0S ight |}^2}=frac{sqrt{A^2+B^2}}{left | A ight | left | B ight |} left | Ax_0+By_0+C ight | end{aligned}$

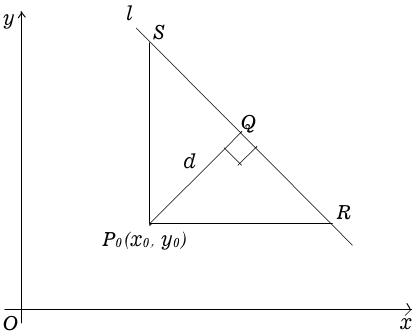
设 (left | P_0Q ight |=d) ，由三角形面积公式可得

[dcdot left | RS ight |=left | P_0R ight |cdot left | P_0S ight | ]

于是得

[d=frac{left |P_0R ight |cdot left | P_0S ight |}{RS}=frac{left | Ax_0+By_0+C ight |}{sqrt{A^2+B^2}} ]

因此，点 (P_0(x_0，y_0)) 到直线 (l: Ax+By+C=0) 的距离

[d=frac{left | Ax_0+By_0+C ight |}{sqrt{A^2+B^2}} (A，B不能同时为0) ]

例5 求点 (P_0(-1，2))到直线 (l:3x=2) 的距离。
解：

[d=frac{left |3 imes (-1))-2 ight |}{sqrt{3^2+0^2}}=frac{5}{3} ]