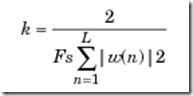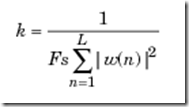功率谱和频谱:
功率谱:信号自相关后FFT
频谱:信号直接FFT
功率谱:
信号的传播都是看不见的,但是它以波的形式存在着,这类信号会产生功率,单位频带的信号功率就被称之为功率谱。它可以显示在一定的区域中信号功率随着频率变化的分布情况。
功率谱可以从两方面来定义:
一个 是自相关函数的傅立叶变换;(维纳辛钦定理)
另一个 是时域信号傅氏变换模平方然后除以时间长度。(来自能量谱密度) 根据parseval定理,信号傅氏变换模平方被定义为能量谱,能量谱密度在时间上平均就得到了功率谱。 频谱:
频谱是常常指信号的Fourier变换。 (1-7 作者:Yorkxu)转载的理解:
(1)信号通常分为两类:能量信号和功率信号;
能量信号:又称能量有限信号,是指在所有时间上总能量不为零且有限的信号。 功率信号:它的能量为无限大,它对通信系统的性能有很大影响,决定了无线系统中发射机的电压和电磁场强度。
(2)一般来讲,能量信号其傅氏变换收敛(即存在),而功率信号傅氏变换通常不收敛(当然,若信号存在周期性,可引入特殊数学函数(Delta)表征傅氏变换的这种非收敛性);
(3)信号是信息的搭载工具,而信息与随机性紧密相关,所以实际信号多为随机信号,这类信号的特点是状态随机性随时间无限延伸,其样本能量无限。换句话说,随机信号(样本)大多属于功率信号而非能量信号,它并不存在傅氏变换,亦即不存在频谱;
(4)若撇开搭载信息的有用与否,随机信号又称随机过程,很多噪声属于特殊的随机过程,它们的某些统计特性具有平稳性,其均值和自相关函数具有平稳性。对于这样的随机过程,自相关函数蜕化为一维确定函数,前人证明该确定相关函数存在傅氏变换;
(5)能量信号频谱通常既含有幅度也含有相位信息;幅度谱的平方(二次量纲)又叫能量谱(密度),它描述了信号能量的频域分布;功率信号的功率谱(密度)描述了信号功率随频率的分布特点(密度:单位频率上的功率),业已证明,平稳信号功率谱密度恰好是其自相关函数的傅氏变换。对于非平稳信号,其自相关函数的时间平均(对时间积分,随时变性消失而再次退变成一维函数)与功率谱密度仍是傅氏变换对;
(6)实际中我们获得的往往仅仅是信号的一段支撑,此时即使信号为功率信号,截断之后其傅氏变换收敛,但此变换结果严格来讲不属于任何“谱”(进一步分析可知它是样本真实频谱的平滑:卷积谱);
(7)对于(6)中所述变换若取其幅度平方,可作为平稳信号功率谱(密度)的近似,是为经典的“周期图法”;
补充:(8) 一个信号的频谱,只是这个信号从时域表示转变为频域表示,只是同一种信号的不同的表示方式而已;而功率谱是从能量的观点对信号进行的研究,其实频谱和功率谱的关系归根揭底还是信号和功率,能量等之间的关系。
谱估计 功率谱估计一般分成两大类: 经典谱估计,也称为非参数谱估计。 现代谱估计,也称为参数谱估计。

clc;close all;clear all;
[s, fs] = audioread('hello.wav');%s=166912*1;fs=44100
%命令说明:[y,Fs] = audioread(filename):returns sampled data, y, and a sample rate for that data, Fs.
%sound(y,fs) % set analysis parameters, pre-emphasise and windowing %根据话音位置,取5000可以把话音主要部分加入其中
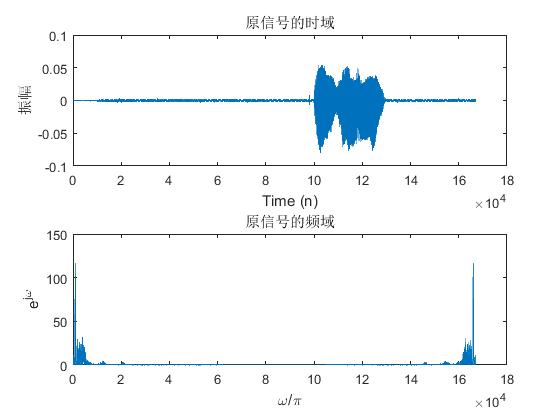
figure; subplot(2,1,1); plot(s); ylabel('振幅'); xlabel('Time (n)'); title('原信号的时域'); Xk=fft(s);
subplot(212);plot(abs(Xk)); xlabel('omega/pi');ylabel('e^j^omega');title('原信号的频域');
%===============================================================
N = 4000;
Nfft = 4000;
n0 = 10000;
x = s(n0 : n0+N-1);%从10000个点截到14000,共4000个点
x1 = filter([1 -0.97], 1,x); %预加重 滤波器 %filter:Y = FILTER(B,A,X) ,输入X为滤波前序列,Y为滤波结果序列,B/A 提供滤波器系数,B为分子, A为分母
%整个滤波过程是通过下面差分方程实现的: %a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + … + b(nb+1)*x(n-nb)-a(2)*y(n-1) - a(3)*y(n-2) + … + a(nb+1)*y(n-nb)
%作用:消除6dB/oct(分贝/倍频程)的跌落,使语音信号的频谱变得平坦。
w = (window('hamming', N)); xw = x1 .* w; %加窗 % Estimate PSD of the short-time segment
Sxw = fft(xw, Nfft);
Sxdb = 20*log10(abs(Sxw(1 : Nfft/2))) - 10*log10(N); %Sxdb 功率谱:时域fft取模平方后除以信号的长度 转换成db
figure;
subplot(311);
plot(x);ylabel('振幅'); xlabel('Time (n)'); title('截取信号的时域信号');
subplot(312);
plot(x1);ylabel('振幅');xlabel('Time(n)');title('截取信号通过filter预处理后的时域信号');
subplot(313);
plot(xw);ylabel('振幅'); xlabel('Time (n)'); title('截取信号加汉明窗后的时域信号');

%============================================================================
figure;
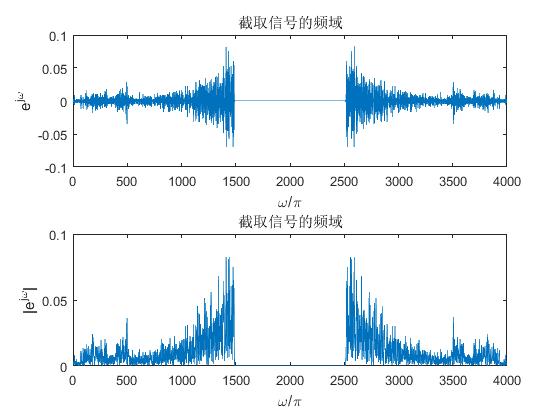
subplot('211');plot(1:Nfft,Sxw); xlabel('omega/pi');ylabel('e^j^omega');title('截取信号的频域');
subplot(212);plot(1:Nfft,abs(Sxw)); xlabel('omega/pi');ylabel('|e^j^omega|');title('截取信号的频域');
%============================================================================
figure;
subplot(211);
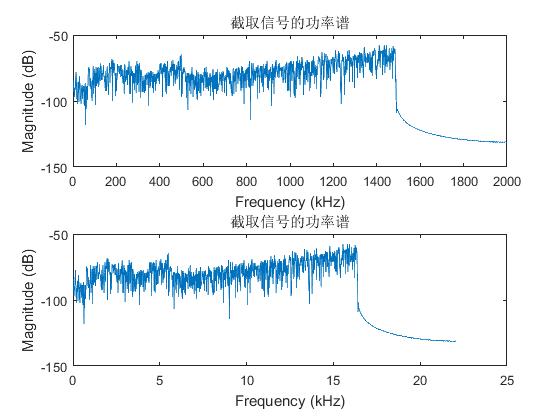
plot(Sxdb); %横轴1-2000
ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)');title('截取信号的功率谱');
subplot(2,1,2); f1 = (0 : Nfft/2-1)*fs / Nfft / 1000;%取前一半 后一半是翻转,不必考虑
plot(f1, Sxdb); ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)');title('截取信号的功率谱');
====================================================================================================================================
经典谱估计法1:相关图法
为了减少谱估计的方差,采用长度为2M-1的窗函数对自相关函数进行截取(联系上式),得
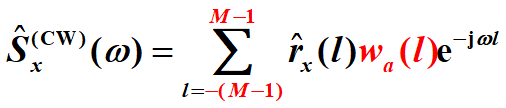
![]()
可使用矩形窗和三角窗。
估计自相关序列:
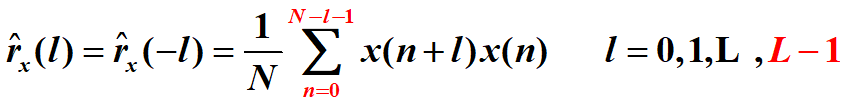
这里解释一下,下标之所以是0~L-1 且r关于l=0对称,是因为数学推导:把-l带入r(l)依然能得到后面式子的结果。(问的老师)
构成加窗自相关序列:
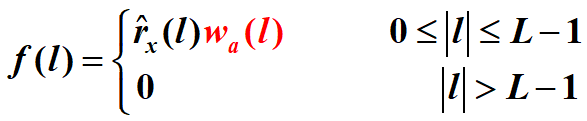
关于自相关的补充:
计算序列 f(l) 的NFFT(一般选NFFT >2L-1)点DFT/FFT,即为功率谱估计的采样值:
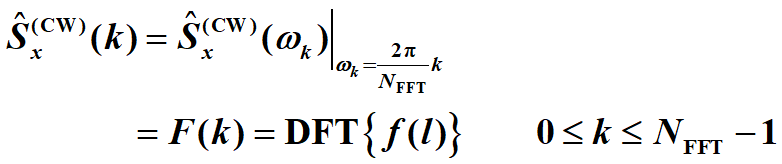
%进一步处理
r = zeros(2*N/2-1, 1);%(-(N/2-1)~(N/2-1))共2L-1个点 计算自相关%3999*1 %这个不是完全的自相关,只是一半的自相关
for k = 1 : N/2 %从1到2000循环
x1 = x(k : N); %从k到4000
x2 = x(1 : N+1-k); %从1到4001-k
r(N/2+k-1) = x1' * x2 / N;
r(N/2-k+1) = r(N/2+k-1); %r(-k) = r(k)
end
rx = r ;
Sxz1 = fft(rx, Nfft); %DFT
Sxdbz1 = 10*log10(abs(Sxz1(1 : Nfft/2)));%转换成db
figure;
subplot(211);
plot(1:Nfft,abs(Sxz1)); ylabel('|e^j^omega|');xlabel('omega/pi');title('相关图法');
subplot(212); plot(f1, Sxdbz1); ylabel('振幅 (dB)'); xlabel('频率 (kHz)');title('相关图法(矩形窗)‘);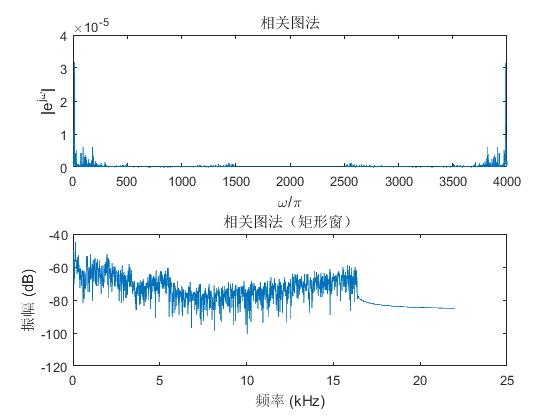
%=======================================================================================
w = triang(2*N/2-1)'; %三角窗 加窗后效果
rx = r .* w';
Sxz2 = fft(rx, Nfft);
Sxdbz2 = 10*log10(abs(Sxz2(1 : Nfft/2)));
figure;
plot(f1, Sxdbz2);
ylabel('振幅 (dB)'); xlabel('频率 (kHz)');
title('相关图法----加三角窗后');

经典谱估计法2:周期图法
由本文开始给的定义,功率谱的计算可以是时域信号傅氏变换模平方然后除以时间长度。

但是此方法,当周期图的方差(当N较大时),方差:
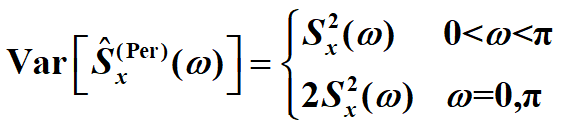
(可以用多次实验取平均来缓解) 改进:
- 多个周期图求平均 把数据记录切分为K个分段,分别求周期图,然后求平均。每段长L,偏移量D
![]()
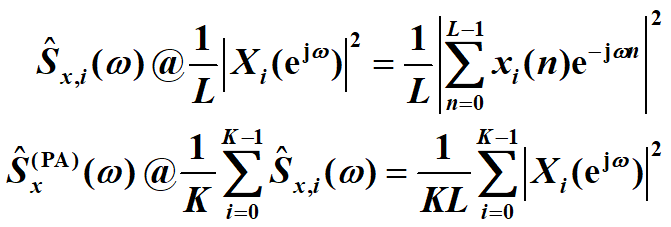
(上式@号其实是=号) PA: 周期图求平均;
Bartlett方法:D=L; Welch方法: D=L/2
Bartlett方法就是把数据分D段,每段fft模平方除以每段长度,再把D段的s相加再平均。
Welch方法就是有重复的分段,具体如下图:

%----------------周期图法 Bartlett谱估计--------------%
Sx = zeros(1, Nfft/2);K = 4; L = N/K; %Sx:2000*1 ,L=1000
for k = 1 : K
ks = (k-1)*L + 1; %k=1,ks=1; k=2,ks=1001;
ke = ks + L - 1; %k=1,ke=1000 ;k=2,ke=2000;
X = fft(x(ks:ke), Nfft);
X = (abs(X)).^2; %周期图法这里要abs + 平方 注意
for i = 1 : Nfft/2 %i=1:2000
Sx(i) = Sx(i) +X(i);
end
end
for i = 1 : Nfft/2
Sx(i) = 10*log10(Sx(i)/(K*L));
end
figure; %
subplot(4,1,1); plot(f1, Sx); ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)'); title('Bartlett Estimate, N=4000, K=4, D=L=1000')
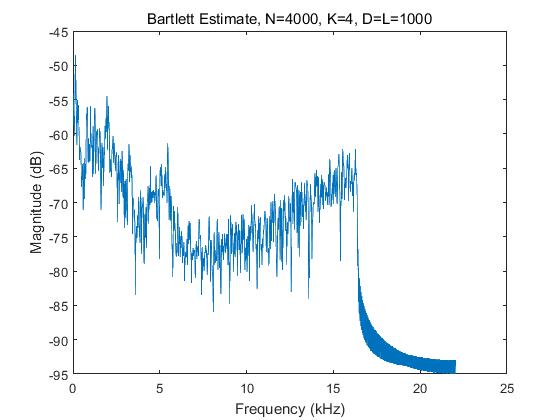
%----------------周期图法 Welch谱估计--------------%
Nfft = 4000; K = 8; D = fix(Nfft/2 / (K+1));%fix:向0方向靠拢取整 分为K+1格,可以重叠K次做fft %D=222
L = 2*D; %L=444
Sxw = zeros(1, Nfft/2); %1*2000
w = (window('hamming', L))'; %1*444
for k = 1 : K %1*8
ks = (k-1)*D + 1; %k=1,ks=1;k=2,ks=223;k=3,ks=445;k=4,ks=667; k=8,ks=1555
ke = ks + L; %k=1,ke=445;k=2,ke=667 k=8,ke=1999
xk = x(ks:ke)*w; %时域加窗 %k=1,444*1 1*444
X = fft(xk, Nfft);
X = (abs(X)).^2;
for i = 1 : Nfft/2
Sxw(i) = Sxw(i) + X(i); %这里只取前N/2个点 因为后N/2个点是前的翻转
end
end
for i = 1 : Nfft/2
Sxw(i) = 10*log10(Sxw(i)/(K*L)); %转换成db
end
figure;
plot(f1, Sxw); ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)'); title('Welch Estimate, N=4000, K=4, D=222, L=444');

语谱图
语音信号的时频分布为定义在二维空间的函数,把时频分布画成二维灰度图像的形式,即为语谱图。
MATLAB 函数 [S, f, t, P] = spectrogram(x, window, noverlap, nfft, fs); 效果图
%--------------语谱图--------------%
bw = 300;
nwin = round(2*fs/bw); %nfft = 512;
nfft = 1024;
xy = filter([1 -0.97], 1, s);
noverlap = nwin - round(length(s) / 500);
% compute and show
figure;
[S, f, t, P] = spectrogram(xy, nwin, noverlap, nfft, fs);
surf(t, f/1000, 10*log10(abs(P)), 'EdgeColor', 'none');
axis xy; axis tight; colormap(jet); view(0, 90); xlabel('Time (s)'); ylabel('Frequency (kHz)');
%title('Broadband Spectrogram');
title('Narrowband Spectrogram');
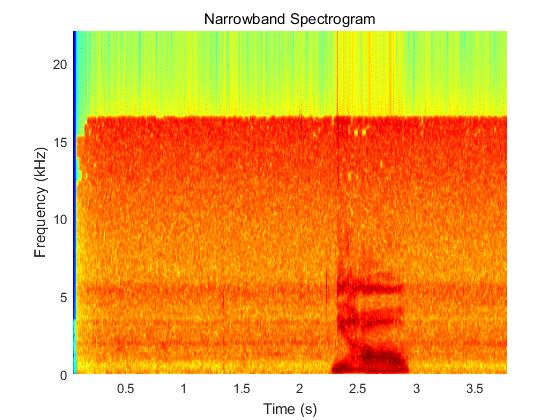
spectrogram
功能:使用短时傅里叶变换得到信号的频谱图。
语法:
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
说明:当使用时无输出参数,会自动绘制频谱图;有输出参数,则会返回输入信号的短时傅里叶变
换。当然也可以从函数的返回值S,F,T,P绘制频谱图,具体参见例子。
参数:
x---输入信号的向量。默认情况下,即没有后续输入参数,x将被分成8段分别做变换处理,
如果x不能被平分成8段,则会做截断处理。默认情况下,其他参数的默认值为
window---窗函数,默认为nfft长度的海明窗Hamming
noverlap---每一段的重叠样本数,默认值是在各段之间产生50%的重叠
nfft---做FFT变换的长度,默认为256和大于每段长度的最小2次幂之间的最大值。
另外,此参数除了使用一个常量外,还可以指定一个频率向量F
fs---采样频率,默认值归一化频率
Window---窗函数,如果window为一个整数,x将被分成window段,每段使用Hamming窗函数加窗。
如果window是一个向量,x将被分成length(window)段,每一段使用window向量指定的
窗函数加窗。所以如果想获取specgram函数的功能,只需指定一个256长度的Hann窗。
Noverlap---各段之间重叠的采样点数。它必须为一个小于window或length(window)的整数。
其意思为两个相邻窗不是尾接着头的,而是两个窗有交集,有重叠的部分。
Nfft---计算离散傅里叶变换的点数。它需要为标量。
Fs---采样频率Hz,如果指定为[],默认为1Hz。
S---输入信号x的短时傅里叶变换。它的每一列包含一个短期局部时间的频率成分估计,
时间沿列增加,频率沿行增加。
如果x是长度为Nx的复信号,则S为nfft行k列的复矩阵,其中k取决于window,
如果window为一个标量,则k = fix((Nx-noverlap)/(window-noverlap))
如果window为向量,则k = fix((Nx-noverlap)/(length(window)-noverlap))
对于实信号x,如果nfft为偶数,则S的行数为(nfft/2+1),如果nfft为奇数,
则行数为(nfft+1)/2,列数同上。
F---在输入变量中使用F频率向量,函数会使用Goertzel方法计算在F指定的频率处计算频谱图。
指定的频率被四舍五入到与信号分辨率相关的最近的DFT容器(bin)中。而在其他的使用nfft
语法中,短时傅里叶变换方法将被使用。对于返回值中的F向量,为四舍五入的频率,其长度
等于S的行数。
T---频谱图计算的时刻点,其长度等于上面定义的k,值为所分各段的中点。
P---能量谱密度PSD(Power Spectral Density),对于实信号,P是各段PSD的单边周期估计;
对于复信号,当指定F频率向量时,P为双边PSD。
P矩阵的元素计算公式如下P(I,j)=k|S(I,j)|2,其中的的k是实值标量,定义如下
对于单边PSD,计算公式如下,其中w(n)表示窗函数,Fs为采样频率,在0频率和奈奎斯特
频率处,分子上的因子2改为1;
对于双边PSD,计算公式如下
如果采样频率没有指定,分母上的Fs由2*pi代替。
spectrogram(...)当调用函数时没有输出参数,将会自动绘制各段的PSD估计,绘制的命令如下
surf(T,F,10*log10(abs(P)));
axis tight;
view(0,90);
spectrogram(...,'freqloc')使用freqloc字符串可以控制频率轴显示的位置。当freqloc=xaxis
时,频率轴显示在x轴上,当freqloc=yaxis时,频率轴显示在y轴上,默认是显示在x轴
上。如果在指定freqloc的同时,又有输出变量,则freqloc将被忽略。
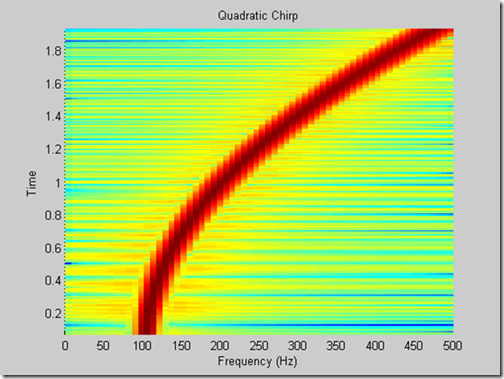
例.计算并显示二次扫频信号的PSD图,扫频信号的频率开始于100Hz,在1s时经过200Hz
T = 0:0.001:2;
X = chirp(T,100,1,200,'q');
spectrogram(X,128,120,128,1E3);
title('Quadratic Chirp');
参考:
https://blog.csdn.net/qq_38559814/article/details/86521602
https://blog.csdn.net/bluehatihati/article/details/84097955
spectrogram函数做短时傅里叶分析:https://blog.csdn.net/zhuguorong11/article/details/77801977