Day3 -- Find Eventual Safe States

Find Eventual Safe States

---

• from : https://leetcode.com/
• mode : random pick
• detail : https://leetcode.com/problems/find-eventual-safe-states/
• degree : Medium

---

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph. If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node. More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe? Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph. The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
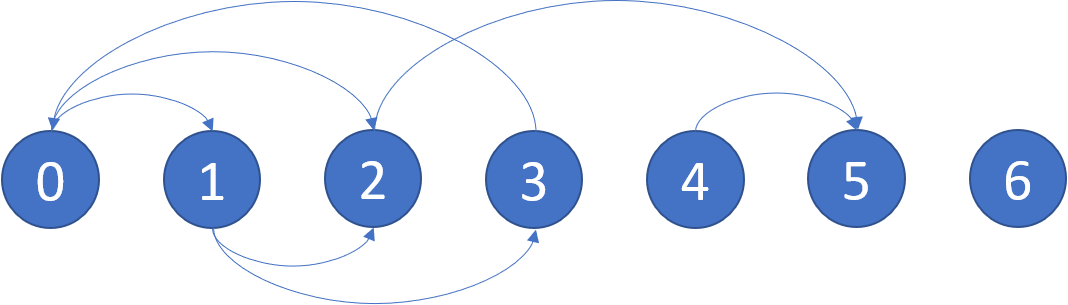
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

Note:

graph will have length at most 10000.
The number of edges in the graph will not exceed 32000.
Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

solution:

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time    : 2018/11/22 


class Solution:
    def __init__(self, graph):
        self.graph = graph
        self.safe = []

    def eventualSafeNodes(self):
        """
        :type graph: List[List[int]]
        :rtype: List[int]
        """
        for i in range(len(self.graph)):
            print "for", i
            req = self.temp(i)
            print "res", req
            if req == 1:
                self.safe.append(i)
        return self.safe

    def temp(self, i, step_node=None):
        if not step_node:
            step_node = []
        if i in step_node:
            return 0
        else:
            step_node.append(i)
            if not self.graph[i]:
                return 1
            else:
                for j in self.graph[i]:
                    if not self.temp(j, step_node):
                        return 0
                return 1


if __name__ == '__main__':
    s = Solution([[1,2],[2,3],[5],[0],[5],[],[]])
    s.eventualSafeNodes()
    print "req", s.safe

总结

• 解题的关键点是节点的的子节点不能进入任何一个循环
• 节点状态判断：我的算法是直接循环判断
• 官网的深度优先判断定义了黑白灰三状态