最小二乘拟合

来自：某小皮

最优化函数库Optimization

优化是找到最小值或等式的数值解的问题。scipy.optimization子模块提供函数最小值，曲线拟合和寻找等式的根的有用算法。

最小二乘拟合

假设有一组实验数据（xi, yi），事先知道它们之间应该满足某函数关系yi = f(xi)，通过这些已知的信息，需要确定函数f的一些参数。例如，如果函数f是线性函数f(x) = kx + b，那么参数k和b就是需要确定的值。

如果用p表示函数中需要确定的参数，那么目标就是找到一组p，使下面的函数s的值最小：

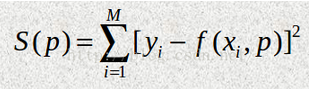
这种算法被称作最小二乘拟合(Least-square fitting)。

使用leastsq()进行最小二乘拟合计算。leastsq()只需要将计算误差的函数和待确定参数的初始值传递给它即可。

leastsq()函数传入误差计算函数和初始值，该初始值将作为误差计算函数的第一个参数传入；

计算的结果r是一个包含两个元素的元组，第一个元素是一个数组，表示拟合后的参数k，b；第二个元素如果等于1，2，3，4中的其中一个整数，则拟合成功，否则将返回mesg。

leastsq函数：

leastsq(func, x0, args=(), Dfun=None, full_output=0, col_deriv=0, ftol=1.49012e-08, xtol=1.49012e-08, gtol=0.0, maxfev=0, epsfcn=0.0, factor=100, diag=None, warning=True) 

一般我们只要指定前三个参数：

• func 是我们自己定义的一个计算误差的函数，
• x0 是计算的初始参数值
• args 是指定func的其他参数

注意：传入leastsq函数的参数可以有多个，但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。

最小二乘拟合示例：

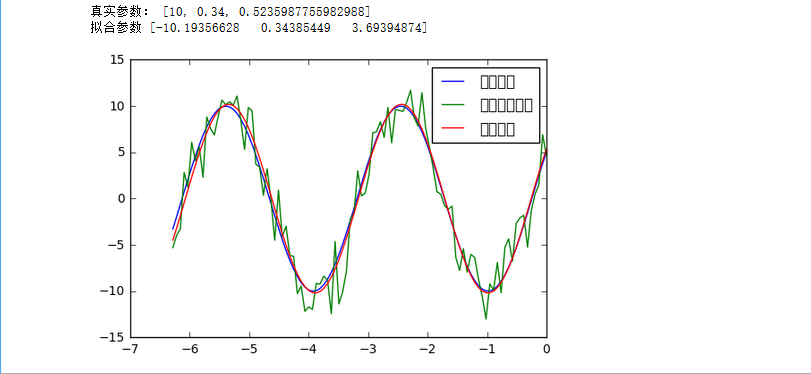
使用最小二乘对带噪声的正弦波数据进行拟合：

拟合得到的参数虽然和实际的参数有可能完全不同，但是由于正弦函数具有周期性，实际上拟合的结果和实际的函数是一致的。

import numpy as np
from scipy.optimize import leastsq

#待拟合的函数，x是变量，p是参数
def fun(x, p):
    a, b = p
    return a*x + b

#计算真实数据和拟合数据之间的误差，p是待拟合的参数，x和y分别是对应的真实数据
def residuals(p, x, y):
    return fun(x, p) - y

#一组真实数据，在a=2, b=1的情况下得出
x1 = np.array([1, 2, 3, 4, 5, 6], dtype=float)
y1 = np.array([3, 5, 7, 9, 11, 13], dtype=float)

#调用拟合函数，第一个参数是需要拟合的差值函数，第二个是拟合初始值，第三个是传入差值函数的其他参数
r = leastsq(residuals, [1, 1], args=(x1, y1))

#打印结果，r[0]存储的是拟合的结果，r[1]、r[2]代表其他信息
print(r[0])

运行结果：[ 2. 1.]

import numpy as np
import pylab as pl
from scipy.optimize import leastsq

def func(x, p):
    # 数据拟合所用的函数：A*sin(2*pi*k*x + theta)
    A, k, theta = p
    return A*np.sin(2*np.pi*k*x + theta)
def residuals(p, y, x):
    # 真实数据x, y和拟合数据之间的误差，p为待拟合参数
    return y - func(x, p)

x = np.linspace(-2*np.pi, 0, 100)

A, k, theta = 10, 0.34, np.pi/6     　　 # 真实数据的函数参数
y0 = func(x, [A, k, theta])          　　# 真实数据
y1 = y0 + 2 * np.random.randn(len(x))　　# 加入噪声之后的实验数据

p0 = [7, 0.2, 0]    # 第一次猜测的函数拟合参数

# 调用leastsq进行数据拟合，
# residuals为我们自己定义的需要拟合的差值函数
# p0为拟合初始值，
# args为传入差值函数的其他参数
plsq = leastsq(residuals, p0, args = (y1, x))

"""
除了初始值之外，还调用了args参数，用于指定residuals中使用到的其他参数（直线拟合是直接使用X,Y的全局变量），
同样也返回一个元组，第一个元素为拟合后的参数数组；
这里将（y1, x）传递给args参数。Leastsq()会将这两个额外的参数传递给residuals()。
因此residuals()有三个参数，p是正弦函数的参数，y和x是表示真实数据的数组。
"""

print(u"真实参数：", [A, k, theta])
print(u"拟合参数", plsq[0])    # 实验数据拟合后的参数
pl.plot(x, y0, label = u"真实数据")
pl.plot(x, y1, label = u"带噪声的数据")
pl.plot(x, func(x, plsq[0]), label = u"拟合数据")
pl.legend()
pl.show()

 运行结果：