学习支持向量机的一点感悟

本文作者Key,博客园主页：https://home.cnblogs.com/u/key1994/

本内容为个人原创作品，转载请注明出处或联系：zhengzha16@163.com

1.Introduction

接下来是关于支持向量机（SVM）算法的介绍。

我选择SVM作为第一次博客的主要内容，并不是因为我觉得SVM算法优于其他算法，也不是因为我对该算法更了解，而是因为今天在参加Udacity的自动驾驶课程时刚好学习了SVM，所以及时记录下来以便后用。

在学习一种新的算法的时候，我习惯于从了解该算法的提出时间、提出背景等问题来着手，因为这样可以快速了解算法的优势与劣势、应用范围，并方便与其他算法进行比较。这一过程往往需要花费时间来查阅大量的文献，而且对算法的原理、推导等无过多帮助，因此往往被很多学者忽略。尽管如此，我依然会从众多资料中想办法找到我想要的答案。

一般认为，支持向量概念的提出是在20世纪60年代（准确的说是1963年），由Vladimir N. Vapnik and Alexey Ya. Chervonenkis ，而成熟的支持向量机理论则由Cortes和Vapnik在1995年正式发表的Machine Learning中提出的。也就是说，支持向量机虽然提出较早，但是真正实现流行应用是在1995年之后。

最早的支持向量机就是用于解决分类任务，而现在支持向量机也被用于回归任务中。

2.原理推导

现在学习算法其实很简单，只需要在Google或者百度中输入“support vector machine”或者“SVM”或者“支持向量机”，至少可以找到成百上千条搜索结果。我们可以充分利用这些搜索结果来获取我们想要的知识。而众多结果里面，算法的原理推导往往市千篇一律的，所以我觉得在原理推导部分我不需要输入这些重复的内容，只需要在理解的基础上转载别人的成果（或者更简单一点，只需要留下网址）。但是，在这里我还是想要记录一下自己的理解，也就是别人没有提到的知识。

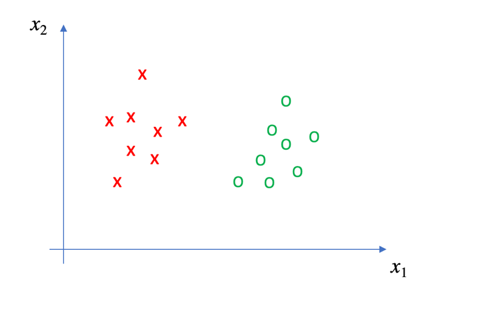
 在这幅图中，我们的任务是对x点和o点进行分类，这个问题看上去如此简单——只需要在x点和o点确定一条直线（在空间中为超平面），即可完成分类。

 

但是可以实现该功能的直线（或者超平面）有很多个，而支持向量机的工作，就是确定最优的那一个。

具体如何实现的呢？

对于每一条直线（或超平面），总存在距离该直线（或超平面）距离（这里的距离如何理解？）最近的一个点，假设该距离分别为l₁和l₂，令

l = l₁ + l₂

在这里我们暂且讨论二维世界的问题。根据支持向量机理论，使l值最大的一条直线即为最优的分类器。实际上，这里的l可以定义为margin，距离最优分类器最近的数据点被称为“支持向量”。

 

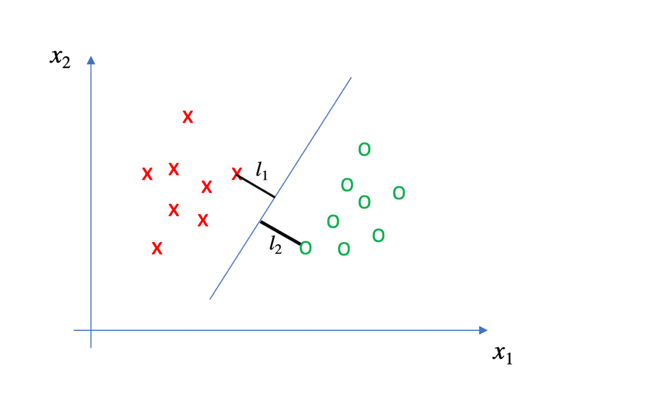
 到目前为止，我们就可以确定支持向量机的分类理论。

但是，在这里我有一个疑问，一旦直线的斜率确定好之后，我们可以在确定两条直线a和b分别经过x点和o点，是否在a和b之间的任意一条直线都是最优分类器呢？因为这些直线的margin都是相同的。

查阅了一些资料，好像都没有讨论这个问题，不禁让我怀疑自己是否没有完全理解支持向量机的实质。但是，这个疑问依然深深印在我的脑海里。

对于我的疑问，我自己也尝试着给出解答。首先，我认为即使在直线a和b之间任意确定一条直线，margin的大小都相同，但是真正的最优分类器只有一个。否则，你认为下图中的c和d直线的分类效果相同吗？

 

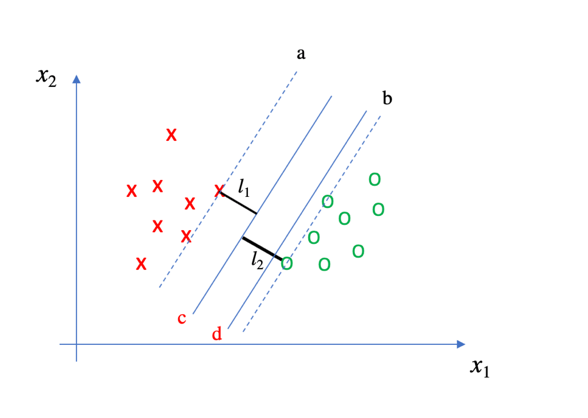
如果给定一个新的o样本点，该样本点有可能会落在直线b的右侧，也有可能会落在左侧。加入落在b的左侧，由于直线d 距离直线b 更近，所以该点就会有更大的概率落在直线d的左侧（注意，此时分类结果是错误的）。而c线距离直线b更远，所以以c线为分类器时，新的样本点被错误分类的概率更小。或者也可以以更专业的名词来概括：c直线构成的分类器鲁棒性更好。至于鲁棒性的概念，这里无须多言。

那么，怎样确定最优分类器的位置呢？以下是我个人的见解。

确定最优分类器的位置，需要充分考虑现有样本点的分布规律。有时候一类样本点可能分布较为紧凑，也可能较为分散。从统计学上来说，可以用方差或者标准差来描述这一特性。如果某类样本点方差更大，则其数据越分散。由于我们假设所有的样本是服从独立同分布的（IID），那么就有理由相信，当给出一个新的数据点时，该数据点的位置不确定性越大。很明显，分类器的位置要距离该类别数据更远，从而保证分类器的鲁棒性。因此，我的解决方法是：

对于已知的样本，分别求出不同类别的样本的方差，这里假设x点样本的方差为V₁，O点的方差为V₂，支持向量机的margin为l，那么最优分类器距离a线的距离为：

 

即：某类型数据点的方差越大，分类器距离该样本集越远。

该方法还有一个优势：在确定直线a和b 的斜率时，我们只用到了距离分类器最近的某些点，而距离分类器较远的数据点没有考虑，甚至在SVM的理论体系下这些点可能永远都用不到。那么这些点是否包含有用的信息呢？我相信是包含的。通过求同类型所有数据点的方差，在一定程度上就可以提取到这些点的有用信息。

以上方法是我自己的一个简单构想，至于方法的效果如何，我现在还来不及验证，只能暂时搁置于此。如果有读者对该方法有不同的看法，或者有意向去验证，欢迎与我联系。再次强调：我只是在做大胆的假设，然后小心的求证。结果可能不甚理想，望海涵。

3.核函数

如果支持向量机的介绍至此为止，那么算法也太过于简单。事实是，以上部分仅仅是为了SVM的理论推导而进行的简化，而现实中的问题复杂得多。例如，对于下图所示的各个点，我们如何运用以上的知识进行分类呢？

 

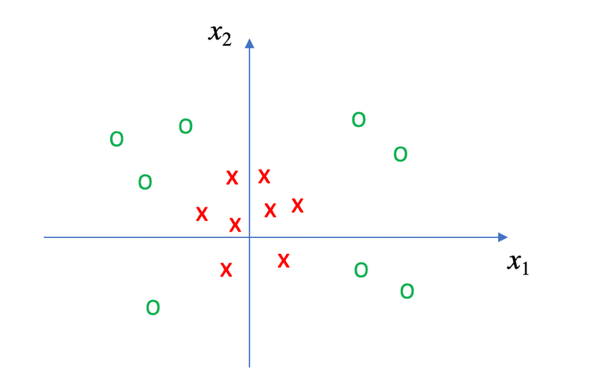
 显然，我们很难找到一条直线将x点和O点完全分开。那此时应该怎么办呢？

首先我们观察一下这些数据点，不难发现x点距离坐标系原点都比较近，而O点则距离原点比较远。如果构建以下函数：

那么就可以将各个数据点在新的x₁-z坐标系中重新分布，如下图所示：

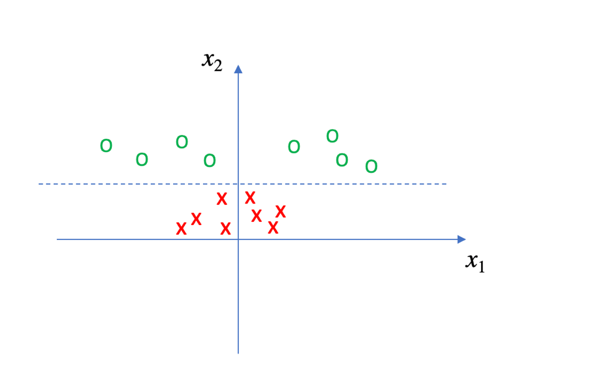
看上去，我们就可以找到一条直线将x点和O点完美分类了。这里的z函数称之为核函数（Kernel），至于为何如此命名，坦白讲我也不知道。

如果你认为核函数的作用就是对数据点进行处理，使其可以线性可分，那么很遗憾的告诉你这种理解是错误的，因为以上例子只是核函数的一种特殊情况。核函数真正的作用是将高维问题中的复杂运算简化为低维运算，从而避免了繁琐的运算，加快分类器的训练速度。想要深入了解核函数，只需要在你的浏览器中输入“核函数”或者“Kernel Function”，即可获得答案。还是之前说的，对于可以轻易找到答案的问题，这里不会花费时间来讲解。

但现在的问题是，如何确定核函数呢？以上的示例是通过肉眼观察出样本点的分布规律，人为构造的的核函数。但是并不是所有的样本点都可以通过肉眼观察出其分布规律。因此，在支持向量机中，人们规定了几种常用的核函数：

  虽然这些函数公式看上去比较吓人，但是如果你认真理解过核函数的定义，这些函数对你来说会非常简单。而且，我们在使用SVM进行分类时，往往借助于python、Matlab等软件来完成训练与预测，在这些软件中，我们只需要从相应的库或者包中调用这些核函数即可，不需要手动输入核函数的公式，应用起来非常方便。

值得一提的是，虽然SVM是目前非常常用且流行的一种算法，但是当我们使用SVM解决实际问题时，往往无法达到100%的准确率。一般来说我们需要规定目标准确率，然后通过不断调整参数，朝着这个目标来努力。当然，我们也要想办法避免出现过拟合（overfitting）。这里的参数主要有以下:

(1)  C: float参数 默认值为1.0

错误项的惩罚系数。C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低，也就是对测试数据的分类准确率降低。相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。

(2) gamma: float参数 默认为auto

核函数系数，只对‘rbf’,‘poly’,‘sigmod’有效。如果gamma为auto，代表其值为样本特征数的倒数，即1/n_features。

gamma表征每一个训练样本对分类器的影响大小。gamma取值越大，则距离分类器较近的点的权重越大，即分类器主要考虑较近的点；gamma取值越小，则距离分类器较远的点权重增大，分类器可以考虑更多样本点的信息。

（3）其他参数

影响SVM分类精度、训练效果、训练时间的因素还有很多，这里不再赘述。可以参照以下网页内容自行学习：

https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html