离散与维灾难

离散与维灾难

1. 连续状态下的MDP

到目前为止，我们主要讲述了在有限状态空间下的MDP，现在我们讨论一下在可能是无限状态空间下的MDP。举个例子说，一辆车，我们可以用(x, y, θ, , , )来表示状态，其中(x,y)表示位置，θ是方向，在x、y方向速度分别为, ，角速度为。因此，S = R⁶，是在无限的状态集合里，因为对于一辆车可能的位置和方向是无限的。相似的，在自主驾驶中，直升飞机在3维空间里，状态空间是9个维度的，且也是状态集合也是无限的。在这部分，我们讨论在状态空间为Rⁿ下的一些求解MDP的方法。

求解连续状态MDP的最简单的方法也许就是离散化状态空间了（有限元），之后采用之前提到的值迭代或策略迭代的方法求解。

举个例子而言，假如我们有一个二维的状态(s₁,s₂)，我们可以用如下方格离散化状态空间。

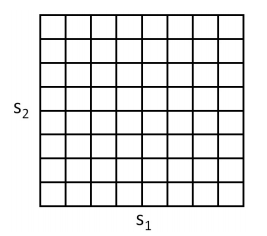
这里每一个网格表示一个离散状态，我们可以采用离散状态空间(, A, {P_¯sa}, γ, R)来近似连续的状态空间，这里是离散状态空间，{P_¯sa}是我们的状态转移概率矩阵。我们可以使用值迭代或者策略迭代求解V^∗(¯s)和π^∗(¯s)。当我们的实际系统状态为某个连续状态s∈ S，我们需要选择一个合适的动作，这个时候我们只要计算s对应的离散状态，就可以得到需要采取的最优动作π^∗(¯s)。

离散化方法可以应用在很多问题中。然而，该方法有两个缺点：第一，他使用了相当朴素代表来表示V^∗(或π^∗)。被逼入说，他假设了对于各个离散化的间隔的值函数是一个常数(比如，在各个网格中，值函数是分段常数)。为了更好的理解这种情况，考虑在监督式学习下的一个问题，拟合一个如下数据集合：

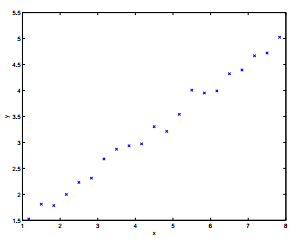
很明显，线性回归能够很好的解决这个问题。然而，如果我们对于x轴采用离散化，之后选用带标点即在每个离散间隔中的分段常数，然后拟合结果如下图：

这里的分段常数代表并不能很好的表示许多平滑的常数。结果并不能很好的平滑这些输入，且不能泛化到其他的不同点。使用这样的代表点法，我们需要一个非常好的有限离散(即采用更小的网格)来取得更好的结果。

另一个问题是这种代表法也被称之为维灾难(curse of dimensionality)。比如S =Rⁿ，我们离散化每一个n维的状态到k个值。那么整个离散空间将会达到kⁿ，状态空间维度指数增长太大而无法扩展到很多大型问题上。比如，我们有一个10维的状态空间，吴国我们离散化每个状态到100个值，那么我们将会得到100¹⁰ = 10²⁰维度离散状态，这么大的空间已经无法在一般的电脑上运行了。

总的来说，在一维或者二维的问题上，离散化方法还是非常有效的方法。有些时候到达4维度状态空间时，选择一个合适的离散化方法也能达到较好的结果。如果你足够幸运和聪明的话，即使在6维问题上，也可能得到到一个不错的结果。但是，如果再高维度，那么基本是没什么希望了。