高斯混合模型

高斯混合模型

1. 高斯混合模型回顾

根据EM的定义，我们重新回顾一下高斯混合中的ϕ，µ和Σ参数拟合。为了简单起见，这里我们在M-步中仅更新φ，µ_j，而把Σ_j的更新留给大家自己推导。

E-步是很容易的，根据上面的推导，我们计算：

w⁽ⁱ⁾_j = Q_i(z⁽ⁱ⁾= j ) = P(z⁽ⁱ⁾= j |x⁽ⁱ⁾; ϕ, µ, Σ)

这里，Q_i(z⁽ⁱ⁾ = j) 表示在概率分布Q_i下，z⁽ⁱ⁾取得j的概率。在M-步，我们需要最大化以ϕ，µ和Σ为参数的似然函数。似然概率为：

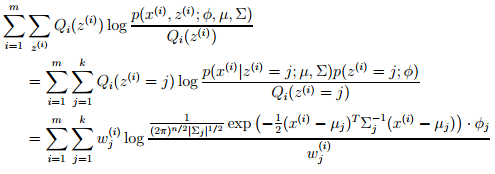
接下来，我们以µ_l为参数，对其取偏导数，结果如下：

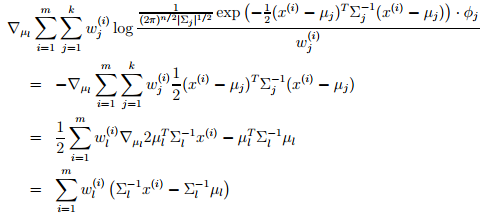
让偏导数结果为0，得到µ_l的更新公式如下，即与我们之前笔记提到的一样。

接下来，再举个M-步中的例子，即更新ϕ_j，这样我们需要最大化的就是。这里有一个限制条件就是所有ϕ_j的和是1，因为ϕ_j = p(z⁽ⁱ⁾=j; ϕ)。为了处理好和为1的限制条件，我们采用拉格朗日法，即

 

这里的β是拉格朗日乘子。取偏导数得到：，让该式子等于1，则得到：。这里正比于，采用限制条件，我们很容易得到 (这里用到了w⁽ⁱ⁾_j = Q_i(z⁽ⁱ⁾= j )和概率和为1，即) 。因此，我们得到了M-步中更新参数ϕ_j的公式：

 

此外，M-步中更新Σ_j的推导也是类似的，不过稍微复杂点，毕竟是矩阵，这里就不再赘述，而之前已经把混合高斯模型的结果给出了。

注：如果将样本看作观察值，潜在类别看作是隐藏变量，那么聚类问题也就是参数估计问题，只不过聚类问题中参数分为隐含类别变量和其他参数。大家可以去联想监督式学习的等等问题了。

1. 因子分析

当我们的数据x⁽ⁱ⁾∈ Rⁿ是根据多个混合高斯分布产生的，那么我们可以根据EM算法拟合该模型。在这样的情况下，我们通常认为我们有足够的数据来区分数据中的多个高斯分布结构。也就是说，我们的训练样本大小m远大于数据的维数n。现在，我们考虑这样的一种情况，即n ≫ m。在这样的问题里，可能很难拟合出一个高斯模型，更别说混合高斯模型了。具体的，对于小于n的m个样本数据，如果我们使用高斯模型，那么采用最大似然估计得到的均值和协方差如下：

，

我们会发现协方差Σ是奇异矩阵，也就是说是Σ^-1不存在的，而且1/|Σ|^1/2= 1/0。而这两项在通常情况下的多元高斯分布(Multivariate Gaussian distribution)中都是需要计算的。解决这个问题的另一个困难是高斯模型中对参数的最大似然估计会导致将所有的概率仿射(Affine，由一个线性变换接上一个平移组成，在拉格朗日对偶中也提到过)到一个数据(这里的数据x满足x= ，对于一些α_i，满足)跨越的空间去。

更一般的说，除非m比n大到一定数量，否则均值和协方差的最大似然估计结果将是很差的。尽管如此，我们仍然希望通过数据来拟合高斯模型，也许能够捕获数据中方差的一些有趣结构，那么我们该怎么做这些呢？在下一部分，我们开始回顾在Σ上的两种可能限制，而之前的Σ都不能在较少的数据上给出一个满意的解决方案。我们接下来要讨论高斯分布的特性，尤其是如何发现边际高斯分布和条件高斯分布（marginal and conditonal distributions of Gaussians）。最后我们展示因子分析模型(factor analysis model)，以及在因子分析模型上应用EM算法。

1. 限制Σ

   如果没有足够的数据来拟合全部的协方差矩阵(covariance matrix)，我们考虑是否可以对的Σ的矩阵大小做一些限制。比如我们会选择拟合一个是对角矩阵(diagonal)的协方差矩阵。在这样的设置下，可以很容易得到对角矩阵Σ是满足：，这里Σ_jj仅仅是协方差的对角位置的值。

   回忆一下高斯分布的概率密度的等高线都是椭圆的(椭圆的中心由μ决定，而形状由Σ决定)，而一个具有对角矩阵Σ的高斯分布，这些椭圆的两个轴就和坐标轴平行了。有些时候，我们会对Σ做进一步的限制，即Σ不仅仅是对角矩阵，而对角线上的值必须都相等，即满足Σ = σ²I，其中I为单位矩阵，σ²是我们的控制参数。这样，σ²可以通过最大似然估计得到：σ² = ，这个模型对应的高斯分布的概率密度等高线图是圆形的(在二维的情况下，而在高维情况就是球体或超球体)。

   如果我们使用数据拟合全部的非限制的协方差矩阵Σ，要求m ≥ n+1，这样才能使得协方差矩阵Σ是非奇异矩阵。而在上面的两个限制下，我们可以得到当m ≥ 2时，就可以得到Σ是非奇异矩阵。

   然而，限制Σ是对角矩阵也意味着模型过程中不同下标的x_i，x_j是相互独立和不相关的。多数情况下，能够捕获到数据中存在的一些有趣的相关关系是非常好的。如果我们使用了上述两个限制中的任何一个，我们都会因为不独立的问题而失败。在后面，我们会讲到因子分析模型，在该模型中使用了比对角矩阵Σ更多的参数且捕获了数据中的一些相关关系，但是又不需要拟合全部的协方差矩阵

2. 边际和条件高斯分布

   在描述因子分析模型之前，我们讨论一下，对一个服从联合多元高斯分布的随机变量，如何寻找它的边际和条件概率。

   假设我们有一个向量的随机变量x，x=[x₁；x₂]，这里的x₁ ∈ R^r ， x₂ ∈ R^s, and x ∈ R^r+s，假设x ∼ N (µ, Σ)，其中 µ = [µ₁； µ₂]，Σ = [Σ₁₁，Σ₁₂ ；Σ₂₁，Σ₂₂]，这里的µ₁ ∈ R^r， µ₂ ∈ R^s， Σ₁₁ ∈ R^r×r， Σ₁₂ ∈ R^r×s，其他依次类推。注意，协方差矩阵是对称的(symmetric)。在我们的假设下，x1和x2是联合的多元高斯分布，那么x1的边际分布是什么呢？我们很容易得出E(x₁) = µ₁，而Cov(x₁) = E[(x₁-µ₁)(x₁-µ₁)] = Σ₁₁，而根据x₁和x₂的联合协方差定义，我们有：

   

   因为多元高斯分布的边际分布仍然是多元高斯分布，因此对于x₁的边际分布为x₁∼ N (µ₁, Σ₁₁)。那么在给定条件x₂的情况下，x₁的概率分布是什么呢？根据多元高斯分布的定义，可以得到x₁|x₂ ∼ N (µ_1|2, Σ_1|2)，其中：

   

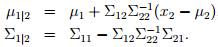
   在下一部分，我们讲述因子分析模型的时候，这些式子都会有帮助的。

3. 因子分析模型

   在因子分析模型中，我们假设(x,z)的联合分布如下，其中z∈ R^k是一个潜在变量：

   z ∼ N (0, I ) x|z ∼ N (µ + Λz, Ψ)

   这里我们模型的参数是µ ∈ Rⁿ，矩阵Λ∈ R^n×k，对角矩阵Ψ∈ R^n×n，其中k的值通常会选择一个小于n的值。这里，我们想象各个数据点x⁽ⁱ⁾是由k维的多元高斯分布z⁽ⁱ⁾抽样产生的；之后通过k维仿射变换µ + Λz⁽ⁱ⁾，将z⁽ⁱ⁾仿射到Rⁿ空间；最后，x⁽ⁱ⁾就是由仿射之后的结果加上一个均值为0，协方差为Ψ的噪声ε，即ε+µ + Λz⁽ⁱ⁾。

   相等的，我们定义因子分析模型如下：z ∼ N (0, I )； ε ∼ N (0, Ψ)；x = µ + Λz + ε；这里的ε和z是相互独立的。现在，我们将要给出我们的模型究竟是什么分布。我们的随机变量z和x有一个联合高斯分布：

   

   现在我们要找出µ_zx和Σ。我们知道E[z]=0，因为z∼ N (0, I)。此外，我们还可以知道：E[x] = E[µ + Λz +ε] = µ + E[Λz] +E[ε] = µ 。把这些放到一起，我们得到：

   

   接下来，为了找到Σ，我们需要计算 Σ_zz = E[(z − E[z])(z − E[z])^T] ( Σ的左上角的部分)，Σ_zx = E[(z − E[z])(x − E[x])^T]( Σ的右上角的部分)，Σ_xx= E[(x − E[x])(x − E[x])^T] ( Σ的右下方部分)。

   现在，因为z∼ N (0, I )，我们可以很容易得到Σ_zz = Cov(z) = I，而且：

   E[(z − E[z])(x − E[x])^T] = E[z(µ + Λz +ε− µ)^T]= E[zz^T]Λ^T+ E[zε^T]= Λ^T

   在这儿的最后一步推导中，用到了E[zz^T] = Cov(z) 和 E[zε^T] = E[z]E[ε^T] = 0(因为z和ε是相互独立的)。相似的，我们可以得到Σ_xx如下：

   E[(x − E[x])(x − E[x])T]     = E[(µ + Λz + ε − µ)(µ + Λz + ε − µ)^T]

   = E[Λzz^TΛ^T+ εz^TΛ^T+ Λzε^T+ εε^T]

   = ΛE[zz^T]Λ^T+ E[εε^T]      = ΛΛ^T+ Ψ

   把这些都放在一起，我们得到了：

   

   因此，我们得到了x的边际分布，x∼N (µ，ΛΛ^T+ Ψ)。因此，在给定训练集合{x⁽ⁱ⁾; i = 1, . . . , m}，我们可以写下参数的最大似然函数如下：

   

   为了进行最大似然估计，我们希望最大化该似然函数。然而，直接进行最大化是很困难的，我们没有学过一个算法能够解决这个闭型解(closed-form)。因此，我们将采用EM算法，在下一部分我们会用EM推导因子分析