时间序列分析
最早的时间序列分析可以追溯到 7000 年前的古埃及。古埃及人把尼罗河涨落的情况逐天记录下来,从而构成一个时间序列。对这个时间序列长期的观察使他们发现尼罗河的涨落非常有规律,由于掌握了涨落的规律,古埃及的农业迅速发展。这种从观测序列得到直观规律的方法即为描述性分析方法。在时间序列分析方法的发展历程中,经济、金融、工程等领域的应用始终起着重要的推动作用,时间序列分析的每一步发展都与应用密不可分。
一般地,人们认为现代时间序列分析起源于英国统计学家 G.u.Yule 在 1927 年提出的 AR(Auto Regressive,自回归)模型。该模型与英国统计学家 G.T.Walker 在 1931 年提出了 MA(Moving Average,移动平均)模型和 ARMA 模型,构成了时间序列分析的基础,至今仍被大量应用。这三个模型主要应用于单变量、同方差场合的平稳序列。
移步平均法(MA)
移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。移动平均法根据预测时使用的各元素的权重不同,可以分为:简单移动平均和加权移动平均。
移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。移动平均法根据预测时使用的各元素的权重不同,可以分为:简单移动平均和加权移动平均。
移动平均法是一种简单平滑预测技术,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。
移动平均法可以分为:简单移动平均和加权移动平均。
简单移动平均
简单移动平均的各元素的权重都相等。简单的移动平均的计算公式如下:
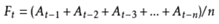
式中, -对下一期的预测值;
-对下一期的预测值;
n--移动平均的时期个数;
 :前期实际值;
:前期实际值;
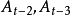 和
和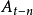 分别表示前两期、前三期直至前n期的实际值。
分别表示前两期、前三期直至前n期的实际值。
加权移动平均法
加权移动平均给固定跨越期限内的每个变量值以不相等的权重。其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以n为周期的周期性变化外,远离目标期的变量值的影响力相对较低,故应给予较低的权重。
加权移动平均法的计算公式如下:
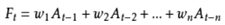
式中,:第t-1期实际销售额的权重;
:第t-2期实际销售额的权重;
:第t-n期实际销售额的权重;
n:预测的时期数;
且
在运用加权平均法时,权重的选择是一个应该注意的问题。经验法和试算法是选择权重的最简单的方法。一般而言,最近期的数据最能预示未来的情况,因而权重应大些。例如,根据前一个月的利润和生产能力比起根据前几个月能更好的估测下个月的利润和生产能力。但是,如果数据是季节性的,则权重也应是季节性的。
存在问题
移动平均法平用于滑常滤波,使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下问题:
1、 加大移动平均法的期数(即加大n值)会使平滑波动效果更好,但会使预测值对数据实际变动更不敏感;
2、 移动平均值并不能总是很好地反映出趋势。由于是平均值,预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动;
3、 移动平均法要由大量的过去数据的记录;
4、它通过引进愈来愈期的新数据,不断修改平均值,以之作为预测值。
移动平均法的基本原理,是通过移动平均消除时间序列中的不规则变动和其他变动,从而揭示出时间序列的长期趋势。
主要特点
1. 移动平均对原序列有修匀或平滑的作用,使得原序列的上下波动被削弱了,而且平均的时距项数N越大,对数列的修匀作用越强。
2. 移动平均时距项数N为奇数时,只需一次移动平均,其移动平均值作为移动平均项数的中间一期的趋势代表值;而当移动平均项数N为偶数时,移动平均值代表的是这偶数项的中间位置的水平,无法对正某一时期,则需要在进行一次相临两项平均值的移动平均,这才能使平均值对正某一时期,这称为移正平均,也成为中心化的移动平均数。
3. 当序列包含季节变动时,移动平均时距项数N应与季节变动长度一致,才能消除其季节变动;若序列包含周期变动时,平均时距项数N应和周期长度基本一致,才能较好的消除周期波动。
4. 移动平均的项数不宜过大。
指数平滑法
指数平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较大的权数放在最近的资料。
指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
指数平滑法的基本公式
指数平滑法的基本公式是:
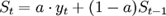
- :时间t的平滑值;
- :时间t的实际值;
- :时间t-1的平滑值;
- a:平滑常数,其取值范围为[0,1];
由该公式可知:
1.是和的加权算数平均数,随着a取值的大小变化,决定和 对的影响程度,当a取1时,;当a取0时,。
2.具有逐期追溯性质,可探源至为止,包括全部数据。其过程中,平滑常数以指数形式递减,故称之为指数平滑法。指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1,远期实际值对本期平滑值影响程度的下降越迅速;平滑常数a越接近于 0,远期实际值对本期平滑值影响程度的下降越缓慢。由此,当时间数列相对平稳时,可取较大的a;当时间数列波动较大时,应取较小的a,以不忽略远期实际值的影响。生产预测中,平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。
3.尽管包含有全期数据的影响,但实际计算时,仅需要两个数值,即和 ,再加上一个常数a,这就使指数滑动平均具逐期递推性质,从而给预测带来了极大的方便。
4.根据公式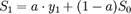 ,当欲用指数平滑法时才开始收集数据,则不存在。无从产生,自然无法据指数平滑公式求出,指数平滑法定义为初始值。初始值的确定也是指数平滑过程的一个重要条件。
,当欲用指数平滑法时才开始收集数据,则不存在。无从产生,自然无法据指数平滑公式求出,指数平滑法定义为初始值。初始值的确定也是指数平滑过程的一个重要条件。
如果能够找到以前的历史资料,那么,初始值的确定是不成问题的。数据较少时可用全期平均、移动平均法;数据较多时,可用最小二乘法。但不能使用指数平滑法本身确定初始值,因为数据必会枯竭。
如果仅有从开始的数据,那么确定初始值的方法有:
1)取等于;
2)待积累若干数据后,取等于前面若干数据的简单算术平均数,如:等等。
指数平滑的预测公式
据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
一次指数平滑预测
当时间数列无明显的趋势变化,可用一次指数平滑预测。其预测公式为:
:t+1期的预测值,即本期(t期)的平滑值
:t期的实际值
:t期的预测值,即上期的平滑值
该公式又可以写作:
一次指数平滑的例子

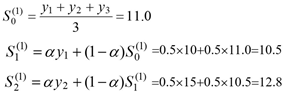


二次指数平滑预测
在实际序列的线性变动部分,指数平滑值出现一定的滞后偏差的程序随着权系数(平滑系数)的增加而减少;但当时间序列的变动出现直线趋势时,用一次指数平滑来进行预测将存在着明显的滞后偏差。因此,也需要进行修正。修正的方法也是在一次指数平滑的基础上再进行二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模式,故称为二次指数平滑法。
在一次指数平滑的基础上得到二次指数平滑的计算公式为:
第t周期的二次指数平滑值
第t周期的一次指数平滑值
第t-1周期的二次指数平滑值
a加权系数(也称为平滑系数)
二次指数平滑是对一次指数平滑值作再一次指数平滑的方法。它不能单独进行预测,必须与一次指数平滑法配合,建立预测的数据模型,然后运用数据模型确定预测值。
二次指数平滑数学模式:
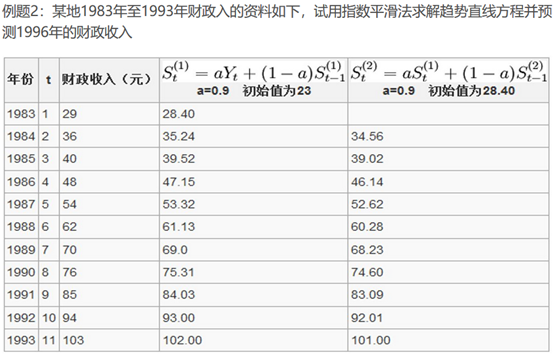

三次指数平滑预测
若时间序列的变动呈现出二次曲线趋势,则需要采用三次指数平滑进行预测。三次指数平滑是在二次指数平滑的基础上再进行一次平滑,其计算公式为:
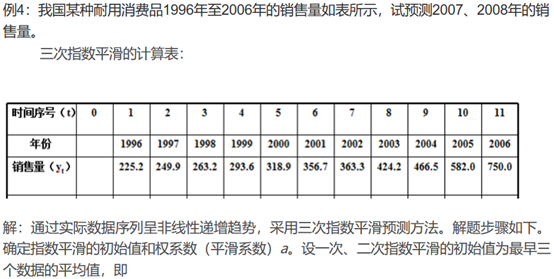

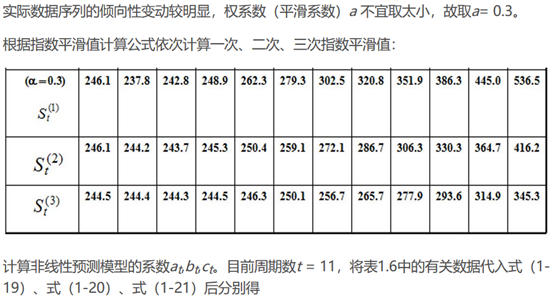

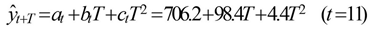



在指数平滑法中,预测成功的关键是a的选择。a的大小规定了在新预测值中新数据和原预测值所占的比例。a值越大,新数据所占的比重就越大,原预测所占的比重就越小,反之亦然。
指数平滑法的缺点:
-
对数据的转折点缺乏鉴别能力,但这一点可通过调查预测法或专家预测法加以弥补。
-
长期预测的效果较差,固多用于短期预测
指数平滑的优点
-
对不同时间的数据的非等权处理比较符合实际情况。
-
使用中仅需选择一个模型参数a即可进行预测,简便易行。
-
具有适应性,也就是说预测模型能自动识别数据模式的变化而加以调整。
自回归法(AR)
自回归和线性回归方法是一样的只是变量是自身相关的。
观测值序列为{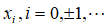 },白噪声序列表示为{
},白噪声序列表示为{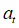 },回归系数用
},回归系数用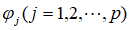 表示,则可得到的AR模型:
表示,则可得到的AR模型:
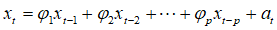 (1)
(1)
设样本观测值{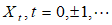 },记
},记
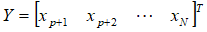

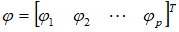
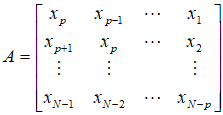
则AR(p)模型可以表示为
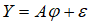 (2)
(2)
由最小二乘原理可得到模型参数的估计为
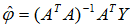
那么根据最小二乘估计值可以得到噪声的估值为
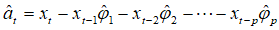
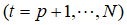
噪声方差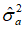 的最小二乘估值为
的最小二乘估值为
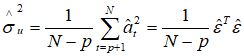
例子如下
某年4月1日至4月12日每天的最低气温如下表示,考虑当前时刻气温与过去时刻气温有关且变化缓慢,因此选用AR(n)模型来拟合日期与最低气温的关系。求:AR(n)模型的阶次以及参数估计值。
|
日期 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
温度 |
10 |
10.4 |
10.6 |
12 |
13.5 |
13.6 |
14.5 |
15.1 |
17.5 |
17.2 |
16.8 |
16.5 |
Matlab求解
L = 12; %数据长度
np = 2; %模型阶次
y = [10 10.4 10.6 12 13.5 13.6 14.5 15.1 17.5 17.2 16.8 16.5]';
yk = zeros(np,1); %多元一次方程的参数
phi = zeros(L,np); %输入数据集向量
for k = 1:L
phi(k,:) = [yk]';
%数据更新
for i = np:-1:2
yk(i) = yk(i-1);
end
yk(1) = y(k);
end
thetae = inv(phi'*phi)*phi'*y %多元一次方程求解参数的公式
自回归-移动平均模型(ARMA)
自回归滑动平均模型(ARMA 模型,Auto-Regressive and Moving Average Model)是研究时间序列的重要方法,由自回归模型(简称AR模型)与滑动平均模型(简称MA模型)为基础"混合"构成。在市场研究中常用于长期追踪资料的研究,如:Panel研究中,用于消费行为模式变迁研究;在零售研究中,用于具有季节变动特征的销售量、市场规模的预测等。
ARMA模型(auto regressive moving average model)自回归滑动平均模型,模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法,适用于很大一类实际问题。它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能,但其参数估算比较繁琐。ARMA模型参数估计的方法很多:
如果模型的输入序列{u(n)}与输出序列{a(n)}均能被测量时,则可以用最小二乘法估计其模型参数,这种估计是线性估计,模型参数能以足够的精度估计出来;
许多谱估计中,仅能得到模型的输出序列{x(n)},这时,参数估计是非线性的,难以求得ARMA模型参数的准确估值。从理论上推出了一些ARMA模型参数的最佳估计方法,但它们存在计算量大和不能保证收敛的缺点。因此工程上提出次最佳方法,即分别估计AR和MA参数,而不像最佳参数估计中那样同时估计AR和MA参数,从而使计算量大大减少。
将预测指标随时间推移而形成的数据序列看作是一个随机序列,这组随机变量所具有的依存关系体现着原始数据在时间上的延续性。一方面,影响因素的影响,另一方面,又有自身变动规律,假定影响因素为x1,x2,…,xk,由回归分析,
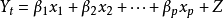
其中Y是预测对象的观测值,Z为误差。作为预测对象Yt受到自身变化的影响,其规律可由下式体现,
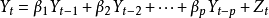
误差项在不同时期具有依存关系,由下式表示,
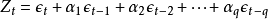
由此,获得ARMA模型表达式:
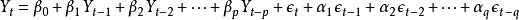
称时间序列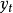 为服从(p,q)阶自回归滑动平均混合模型。或者记为φ(B)
为服从(p,q)阶自回归滑动平均混合模型。或者记为φ(B)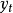
= θ(B)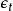
齐次非平稳模型(ARIMA)
ARIMA有一个数据差分过程,是不平稳数据便为平稳的,接下来的原理和ARMA模型一样