单源最短路径
在最短路径问题中,我们给定一个带权重的有向图和权重函数, 该权重函数将每条边映射到实数值的权重上。图中一条路径的权重是构成该路径的所有边的权重之和:
定义从结点u到结点v的最短路径权重如下:
从结点u到结点v的最短路径则定义为任何一条权重为的从u到v的路径p。
最短路径的几个变体
单源最短路径:给定一个图G=(V,E),我们希望找到从给定源结点到每个节点的最短路径。
单目的地最短路径问题:找到从每个节点u到给定目的地节点t的最短路径。如果将图的每条边的方向翻转过来,我们就可以将这个问题转换为单源最短路径问题。
单节点对最短路径问题:找到从给定节点u到给定节点v的最短路径。如果解决了针对单个节点u的单源最短路径问题,那么也就解决这个问题。
所有节点对最短路径问题:对于每个节点u和v,找到从结点u到结点v的最短路径。虽然可以针对每节点运行一遍单源最短路径算法,但通常可以更快地解决这个问题。
初始化
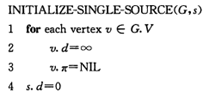
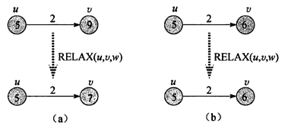
松弛操作

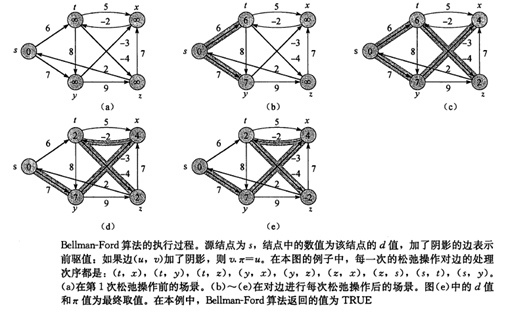
Bellman-Ford算法

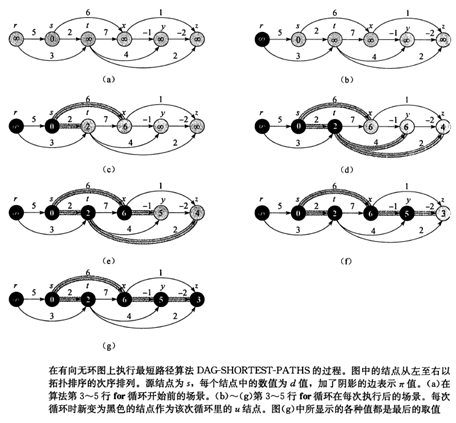
topo sort
有向无环图中的单源最短路径问题
根据节点的拓扑排序次序对带权重的有向无环图G=(V,E)进行边的松弛操作,我们便可以在时间内计算出从单个源结点到所有节点之间的最短路径。在有向无环图中,即使存在权重为负的边,但因为没有权重为负的环路,最短路径都是存在的。
算法首先对有向无环图进行拓扑排序,以便确定结点之间的一个线性次序。以便确定结点之间的一个线性次序。如果有向无环图包含从结点u到结点v的一条路径,则u的拓扑排序的次序中位于结点v的前面。我们只需要按照拓扑排序的次序对结点进行一遍处理即可。每次对一个节点进行处理时,我们对从该节点发出的发出的所有的边进行松弛操作。

Dijkstra算法


三个算法的对比

所有节点对的最短路径问题
Floyd-Warshall算法

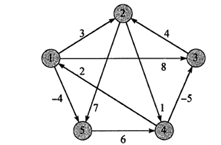
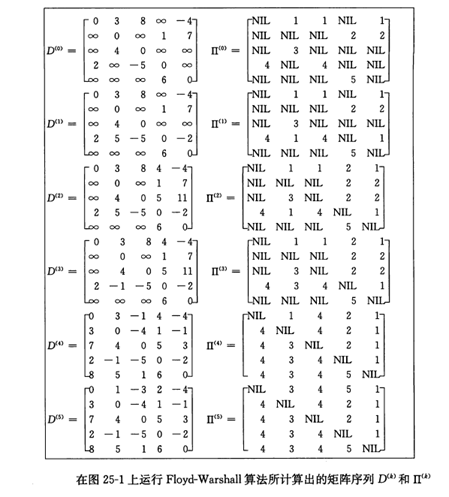
//基本思想是:
//进行中转......允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。
//用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。其实这是一种"动态规划"的思想。