用最少数量的箭引爆气球
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以y坐标并不重要,因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。
一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
Example:
输入:
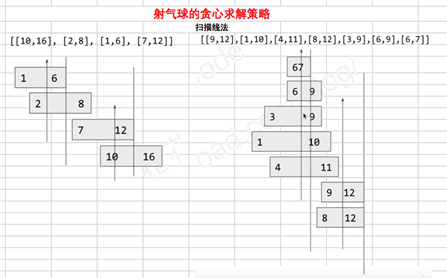
[[10,16], [2,8], [1,6], [7,12]]
输出:
2
解释:
对于该样例,我们可以在x = 6(射爆[2,8],[1,6]两个气球)和 x = 11(射爆另外两个气球)。
思路
1 class Solution { 2 public int findMinArrowShots(int[][] points) { 3 if(points.length==0) 4 return 0; 5 Ballon[] ballons = new Ballon[points.length]; 6 for(int i=0;i<points.length;i++) 7 ballons[i]=new Ballon(points[i][0],points[i][1]); 8 9 Arrays.sort(ballons, new Comparator<Ballon>() { 10 @Override 11 public int compare(Ballon o1, Ballon o2) { 12 return o1.end-o2.end; 13 } 14 }); 15 int ans = 1; 16 int right = ballons[0].end; 17 for(Ballon ballon:ballons) 18 { 19 if(ballon.start>right) 20 { 21 right=ballon.end; 22 ans++; 23 } 24 } 25 return ans; 26 27 } 28 } 29 30 class Ballon{ 31 int start; 32 int end; 33 34 public Ballon(int start, int end) { 35 this.start = start; 36 this.end = end; 37 } 38 }