卷积神经网络各种池化

卷积神经网络各种池化

在卷积神经网络中，我们经常会碰到池化操作，而池化层往往在卷积层后面，通过池化来降低卷积层输出的特征向量，同时改善结果（不易出现过拟合）。图像具有一种"静态性"的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图片，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值（或最大值）来代表这个区域的特征。

mean pooling

计算图像区域的平均值作为该区域池化后的值。

max pooling

选图像区域的最大值作为该区域池化后的值。

Overlapping pooling

重叠池化正如其名字所说的，相邻池化窗口之间会有重叠区域，此时sizeX>stride。

Spatial Pyramid pooling

金字塔池化可以把任何尺度的图像的卷积特征转化成相同维度，这不仅可以让CNN处理任意尺度的图像，还能避免cropping和warping操作，导致一些信息的丢失，具有非常重要的意义。

    一般的CNN都需要输入图像的大小是固定的，这是因为全连接层的输入需要固定输入维度，但是卷积操作是没有对图像尺度有限制，所以作者提出了空间金字塔池化，先让图像进行卷积操作，然后转化成维度相同的特征输入到全连接层，这个可以把CNN扩展到任意大小的图像。

金字塔池化的思想来自于Spatial Pyramid Model,它一个pooling变成了多个scale的pooling。用不同大小池化窗口作用于卷积特征，我们可以得到1*1,2*2,4*4的池化结果，由于conv5中共有256个过滤器，多以得到1个256维的特征，4个256维的特征，以及16个256维的特征，然后把这21个256维特征连接起来输入全连接层，通过这种方式吧不同大小的图像转化成相同维度的特征。

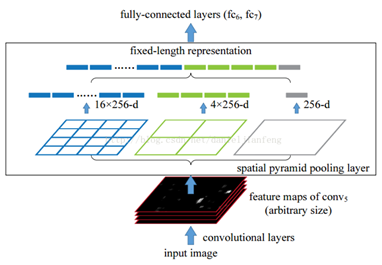
对于不同的图像要得到相同大小的pooling结果，就需要根据图像的大小动态的计算池化窗口的大小和步长。

stochastic pooling

stochastic pooling方法非常简单，只需对feature map中的元素其概率值大小随机选择，即元素值大的被选中的概率也大。而不像max-pooling那样，永远只取那个最大值元素。

假设feature map中的pooling区域元素值如下：

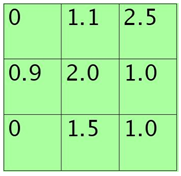
3*3大小的，元素值和sum=0+1.1+2.5+0.9+2.0+1.0+0+1.5+1.0=10

方格中的元素同时除以sum后得到的矩阵元素为：

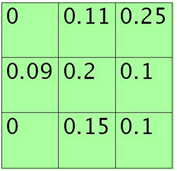
每个元素值表示对应位置处值的概率，现在只需要按照该概率来随机选一个即可。

ROI Pooling faster rcnn

目标检测typical architecture通常可以分为两个阶段：

1. region proposal:给定一张输入image找出objects可能存在的所有位置。这一阶段的输出应该是一系列object可能位置的bounding box。这些通常称之为region proposals或者regions of interest(ROI)
2. final classification:确定上一阶段的每个region proposal是否输入目标一类或者背景。

这个architecture存在的一些问题是：

• 产生大量的region proposals会导致performance problems，很难达到实时目标检测。
• 在处理速度方面是suboptimal
• 无法做到end-to-end training

这就是ROI pooling提出的根本原因。

ROI pooling层可以实现training和testing的显著加速，并提高检测accuary。该层有两个输入：

从具有多个卷积核池化的深度网络中获得的固定大小的feature maps

一个表示所有ROI的N*5的矩阵，其中N表示ROI的数目。第一列表示图像index，其余四列表示其余的左上角和右下角坐标。

ROI pooling的具体操作如下：

1. 根据输入image,将ROI映射到feature map对应位置
2. 将映射后的区域划分为相同大小的sections(sections数量与输出的维度相同)；
3. 对每个sections进行max pooling操作。

这样我们就可以从不同大小的方框得到固定大小的相应的feature maps。值得一提的是，输出的的feature maps的大小不取决于ROI和卷积feature maps大小。ROI pooling最大的好处就在于极大地提高了处理速度。

ROI pooling example

考虑一个8*8大小的feature map,一个ROI，以及输出大小为2*2

1. 输入的固定大小的feature map

   

2. region proposal投影之后的位置（左上角，右下角）：(0,3),(7,8)

   

3. 将其划分为(2*2)个sections(因为输出大小为2*2)，我们可以得到：

   

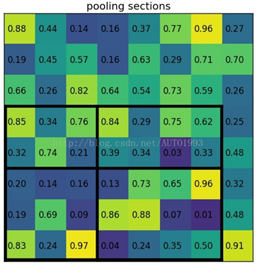
4. 对每个section做max pooling，可以得到：

ROI pooling总结：

1. 用于目标检测任务
2. 允许我们对CNN中的feature map进行reuse
3. 可以显著加速training和testing速度
4. 允许end-to-end的形式训练目标检测系统

自然语言处理中CNN模型中几种常见的Max Pooling操作

转载自：https://blog.csdn.net/malefactor/article/details/51078135

CNN是目前自然语言处理中和RNN并驾齐驱的两种最常见的深度学习模型。下图展示了在NLP任务中使用CNN模型的典型网络结构。一般而言，输入的字或者词用Word Embedding 的方式表达，这样本来一维的文本信息输入就转换成了二维的输入结构，假设输入x包含m个字符，而每个字符的word embedding的长度为d，那么输入就是m*d的二维向量。

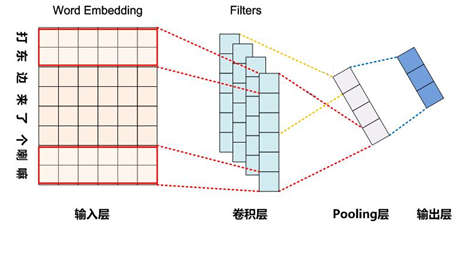
这里可以看出，因为NLP中的句子长度是不同的，所以CNN的输入矩阵大小是不确定的，这取决于m的大小是多少。卷积层本质上是个特征抽取层，可以设定超参数F来指定设立多少个特征抽取器（Filter）,对于某个Filter来说，可以想象有一个k*d大小的移动窗口从矩阵的第一个字开始不断往后移动，其中k是Filter指定的窗口大小，d是word Embedding长度。对于某个时刻的窗口，通过神经网络的非线性变换，将这个窗口的输入值转换为某个特征值，随着窗口不断往后移动，这个Filter对应取得特征值不断产生，形成了这个Filter的特征向量。这就是卷积层抽取特征的过程。每个Filter都如此操作，形成了不同的特征抽取器。Pooling层则对Filter的特征进行降维操作，形成最终的特征。一般在Pooling层之后连接全连接层神经网络，形成最后的分类过程。

可见，卷积核Pooling是CNN中最重要的两个步骤。下面我们重点介绍NLP中CNN模型常见的Pooling操作方法。

Max Pooling Over Time

Max Pooling Over Time是NLP中CNN模型中最常见的一种下采样操作。意思是对于某个Filter抽取到若干特征值，只取其中得分最大的那个值作为Pooling层保留值，其他特征值全部抛弃，值最大代表只保留这些特征中最强的，而抛弃其他弱的此类特征。

    CNN中采用Max Pooling操作有几个好处：首先，这个操作可以保证特征的位置与旋转不变性，因为无论这个强特征在哪个位置出现，都会不考虑其出现的位置而能把它提出来。对于图像处理来说这种位置与旋转不变性是很好的特性，但是对于NLP来说，这个特性其实并不一定是好事，因为在很多NLP的应用场合，特征的出现位置信息是很重要的，比如主语出现位置一般在句子头，宾语一般出现在句子尾等等，这些位置信息其实有时候对于分类任务来说还是很重要的，但是Max Pooling基本把这些信息抛掉了。

    其次，MaxPooling能减少模型参数数量，有利于减少模型过拟合问题。因为经过Pooling操作后，往往2D或者1D数组转换为单一数值，这样对于后续的Convolution层或者全连接层来说无疑当个Filter的参数或者隐藏层神经元个数就减少了。

    再者，对于NLP任务来说，Max Pooling有个额外的好处；在此处，可以把变长的输入X整理成固定长度的输入。因为CNN最后往往会连接全连接层，而其神经元个数是需要事先定好的，如果输入是不定长的很难设计网络结构。前文说过，CNN模型的输入X长度是不确定的，而通过Pooling操作，每个Filter固定取值1个值，那么有多少个Filter，Pooling层就有多少个神经元，这样就可以把全连接层神经元个数固定住，这个有点也是非常重要的。

但是，CNN模型采取MaxPooling Over Time也有一些值得注意的缺点：首先就如上述，特征的位置在这一步骤完全丢失。在卷积层其实是保留了特征的位置信息，但是通过取唯一的最大值，现在在Pooling层只知道这个最大值是多少，但是其出现位置信息并没有保留；另外一个明显的缺陷是：有时候有些强特征会出现多次，比如我们常见的TF.IDF公式，TF就是指某个特征出现的次数，出现次数多说明这个强特征强，但是因为Max Pooling只保留一个最大值，所以即使某个特征出现多次，现在也只能看到一次，就是说同一特征地强度信息丢失了。这是Max Pooling Over Time典型的两个缺陷。

    其实，我们常说的"危机危机"，对这个词汇乐观的解读就是"危险就是机遇"。同理，发现模型的缺点是个好事，因为创新往往就是通过改进模型的缺点而引发出来的。那么怎么改进Pooling层的机制能够缓解上述问题呢？下面两个常见的改进Pooling机制就是干这事情的。

K-Max Pooling

K-MaxPooling的意思是：原先的Max Pooling Over Time从Convolution层一系列特征值中只取最强的那个值，那么我们思路可以扩展一下，K-Max Pooling可以取所有特征值中得分在Top-K的值，并保留这些特征值原始的先后顺序如下下图所示，就是说通过多保留一些特征信息供后续阶段使用。

很显然，K-Max Pooling可以表达同一类特征出现很多次的情形，即可以表达某类特征的强度。另外，因为这些Top K特征值的相对顺序得以保留，所以应该说其保留了部分位置信息，但是这种位置信息只是特征间的相对顺序，而非绝对位置信息。

Chunk-Max Pooling

Chunk-MaxPoooling的思想是：把某个Filter对应的Convolution层的所有特征向量进行分段，切割成若干段后，在每个分段里面各自取得一个最大特征值，比如将某个Filter的特征向量切成3个Chunk，那么就在每个Chunk里面取一个最大值，于是获得3个特征值。如下图所示：

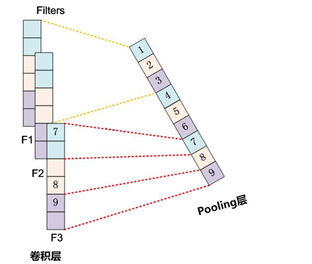
乍一看Chunk-Max Pooling思路类似于K-Max Pooling,因为它也是从Convolution层取出了K个特征值，但是两者的主要区别是：K-Max Pooling是一种全局取Top K特征的操作方式，而Chunk-Max Pooling则是先分段，在分段包含特征数据里面取最大值，所以其实是一种局部Top K的特征抽取方法。

Chunk-Max Pooling很明显也是保留了多个局部Max特征值的相对顺序信息，尽管并没有保留绝对位置信息，但是因为是先划分Chunk再分别取Max值的，所以保留了比较粗粒度的位置信息；当然，如果多次出现强特征，则也可以捕获特征强度。如果分类所需要的关键特征的位置信息很重要，那么类似Chunk-Max Pooling这种能够粗粒度保留位置信息的机制应该能够对分类性能有一定程度的提升作用，但是对于很多分类问题，估计Max-Pooling over time就足够了。