λ演算
λ演算(英文 lambda calculus, λ-calculus)是一套从数学逻辑中发展,以变量绑定和替换的规则,来研究函数如何抽象化定义,函数如何被应用以及递归形式系统。它在20世纪30年代首次发表。Lambda演算作为一种广泛用途的计算模型,可以清晰地定义什么是一个可计算函数,而任何可计算函数都能以这种形式表达和求值,它能模拟单一磁带图灵机的计算过程;尽管如此,Lambda演算强调的是变换规则的运用,而非实现它们的具体机器。
Lambda演算可比拟是最根本的编程语言,它包括了一条变换规则(变量替换)和一条函数抽象化定义的方式。因此普遍公认是一种更接近软件而非硬件的方式。对函数式编程语言造成很大影响,比如Lisp、ML语言和Haskell语言。
Lambda演算包括了建构lambda项,和对lambda项运算归约的操作。在最简单的lambda演算中,只使用以下的规则来构建lambda项:

产生了诸如:(λx. λy.( λz.( λx.zx)( λy.zy))(x,y)的表达式。如果表达式是明确而没有歧义的,则括号可以省略。对于某些应用,其中可能包括了逻辑和数学的常量以及相关操作。
历史
最开始,邱奇试图创制一套完整的形式系统作为数学的基础,当他发现这个系统易受罗素悖论的影响时,就把lambda演算单独分离出来,用于研究可计算性,最终导致了他对判定性问题的否定回答。
非形式化地直觉描述
在λ演算中,每个表达式都代表一个函数,这个函数有一个参数,并且会返回一个值。不论是参数和返回值,也都是一个单参的函数。可以这么说,λ演算中只有一个"类型",那就是这种单参函数。函数是通过λ表达式匿名地定义的,这个表达式说明了函数将对其参数进行什么操作。
例如,"加2"函数f(x)= x + 2可以用lambda演算表示为λx.x + 2(或者λy.y + 2,参数的取名无关紧要),而f(3)的值可以写作(λx.x + 2) 3。函数的应用(application)是左结合的:f x y =(f x) y。
考虑这么一个函数:它把一个函数作为参数,这个函数将被作用在3上:λf.f 3。如果把这个(用函数作参数的)函数作用于我们先前的"加2"函数上:(λf.f 3)(λx.x+2),则明显地,下述三个表达式:
(λf.f 3)(λx.x+2) 与 (λx.x + 2) 3 与 3 + 2
是等价的。有两个参数的函数可以通过lambda演算这样表达:一个单一参数的函数,它的返回值又是一个单一参数的函数(参见柯里化)。例如,函数f(x, y) = x - y可以写作λx.λy.x - y。下述三个表达式:
(λx.λy.x - y) 7 2 与 (λy.7 - y) 2 与 7 – 2
也是等价的。然而这种lambda表达式之间的等价性,无法找到某个通用的函数来判定。
并非所有的lambda表达式都能被归约至上述那样的确定值,考虑
(λx.x x)(λx.x x)
或
(λx.x x x)(λx.x x x)
然后试图把第一个函数作用在它的参数上。(λx.x x)被称为ω 组合子,((λx.x x)(λx.x x))被称为Ω,而((λx.x x x) (λx.x x x))被称为Ω2,以此类推。若仅形式化函数作用的概念而不允许lambda表达式,就得到了组合子逻辑。
动机




lambda演算
lambda演算是由特定形式语法所组成的一种语言,一组转换规则可操作其中的lambda项。这些转换规则被看作是一个等式理论或者一个操作定义。如上节所述,lambda演算中的所有函数都是匿名的,它们没有名称,它们只接受一个输入变量,柯里化用于实现有多个输入变量的函数。
Lambda项
lambda演算的语法将一些表达式定义为有效的lambda演算式,而某一些表达式无效,就像C编程语言中有些字符串有效,有些则不是。有效的lambda演算式称为"lambda项"。
以下三个规则给出了语法上有效的lambda项,如何建构的归纳定义:
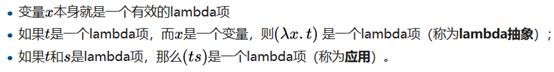
其它的都不是lambda项。因此,lambda项当且仅当可重复应用这三个规则获取时,才是有效的。一些括号根据某些规则可以省略。例如,最外面的括号通常不会写入。


操作函数的函数



