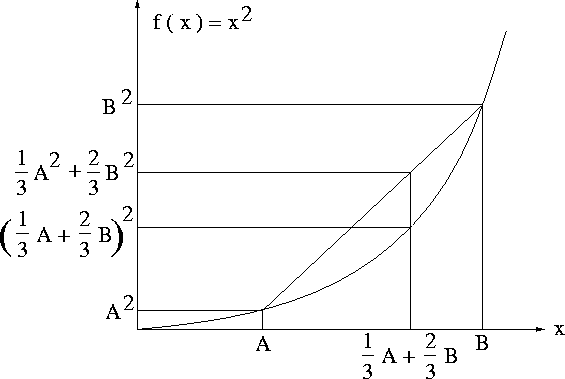Let(设) f be a function with a positive second derivative(二阶导数). Such a function is called “convex"(凸的,注意是向下凸,向上凹,如 x2 ) and satisfies the inequality
| |
inequation (1) relates a function of an average to an average of the function. The average can be weighted, for example,
| |
Figure 1 is a graphical interpretation of inequation (2) for the function f=x2.
|
|
There is nothing special about f=x2, except that it is convex. Given three numbers a, b, and c, the inequality (2) can first be applied to a and b, and then to c and the average of a and b. Thus, recursively, an inequality like (2) can be built for a weighted average(加权平均数) of three or more numbers. Define weights ![]() that are normalized(标准化) (
that are normalized(标准化) (![]() ). The general result(通式) is
). The general result(通式) is
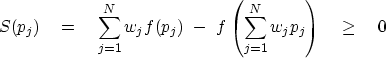 (3) (3) |
If all the pj are the same, then both of the two terms in S are the same, and S vanishes. Hence, minimizing S is like urging all the pj to be identical(完全一样). Equilibrium is when S is reduced to the smallest possible value which satisfies any constraints that may be applicable. The function S defined by (3) is like the entropy(熵) defined in thermodynamics(热力学).