开头借用李航老师书中总结，概率模型有时既含有观测变量，又含有隐藏变量或者潜在变量，如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或者贝叶斯估计法估计模型参数，但是，当模型含有隐含变量的时候，就不能简单的使用这些估计方法，EM算法就是含有隐含变量的概率模型参数的极大似然估计法，或者极大后验概率估计法，一句话总结，EM算法本质上就是用于处理含有隐含变量的模型参数估计的一种方法！
这里第一次看相关文章的童鞋会问，什么是概率模型含有隐含变量啊？举一个例子一下子就可以明白，所谓的隐含变量，就是指进行相关实验时没有直接观测到的变量，或者与试验结果息息相关但是实验过程又没有对其进行记录的随机变量！比如说三枚硬币，A、B、C，进行如下的抛硬币的实验，先抛A硬币，根据A硬币的试验结果来决定接下来是抛B硬币还是C硬币，然后你得到如下的实验结果，比如说：1,1,0,1,1,0,0,0,1,1 且假设只能观测到抛硬币的结果，不能观测到抛硬币的过程，让你估计三枚硬币的模型的参数。这时候，你只观察到了硬币抛完的结果，并不了解A硬币抛完之后，是选择了B硬币抛还是C硬币抛，这时候概率模型就存在着隐含变量！
下面正式进入EM算法的介绍：
1 预备部分 需要了解基本的数学知识，Jason不等式 詹森不等式，具体表述如下：
如果f是凸函数(参考优化理论的定义),X是随机变量，则有：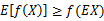 
,如果f是严格的凸函数，当且仅当X是常量的时候，等号成立。
如果用图像来表示的话就是下图：
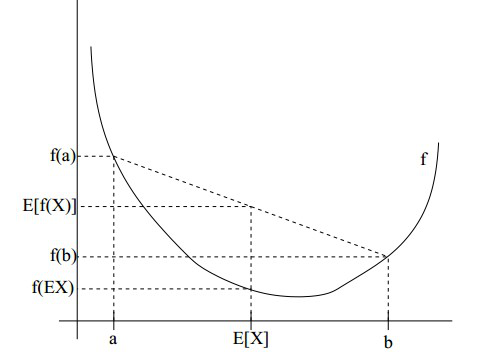（图片并非本人所画，文末会注明来源）
从图中我们可以清晰的看出这个不等式的含义，通俗一点说就是，如果f函数是一个凸函数，那么先取期望后的函数值会小于等于函数值的期望！这一点在后面文章的证明中至关重要。
2 正式介绍
首先来看的是极大似然函数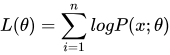 
我们要做的就是根据已知的训练数据去将这个极大似然函数最大化，并且得到最大化的参数θ，但是这种情况下待求参数和观测变量完全混在一起，无法进行求解，所以要再引入一个变量z，就是我们上文中提到的潜在变量，具体公式如下：
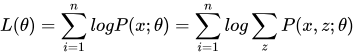很容易发现对等式进行变换之后并不影响结果，这在概率论中是显而易见的！可以直观的解释为，利用模型参数这个条件去估计隐藏变量和观测变量
但是我们发现，经过这样的变换结果还是十分的抽象，因为Z变量实在是太特殊了，假设存在一种Q(z)满足了隐含变量的分布，那么Q(z)必然满足条件： 
.Qi(z)就代表了隐藏变量的某种分布，如果你对观测数据来自于隐藏变量的所有可能性求和，自然得到的结果一定是1,而且，概率一定是大于0的，这样便完美解释了上式！
接下来就是对公式的简化操作:
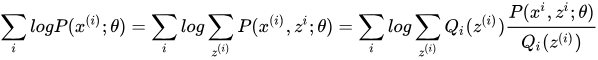
到这一步没什么问题，就是分子分母同时乘以一个Qi(z)，结果不会发生改变，然后观察产生的结果：
这个式子，其实是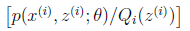
的期望，为什么这么说呢，根据随机过程课本的描述：我们有
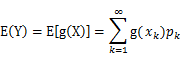，也就是说对一个函数求期望，就是将自变量的概率和自变量对应的函数值相乘然后求和，对于连续变量就是对其求积分，那么，回到我们的式子中来，z(i) 就是自变量， Qi(z)就是其概率值Pk，
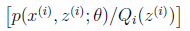就是对应的函数Y，那么产生的结果就可以理解为是一个期望值，从而继续套用我们的詹森不等式进行变换，
，这样我们其实就是得到了极大似然函数的下界函数，再来讨论让等号成立的条件，也就是
当这个'x'是常数的时候，不妨设其等于c，即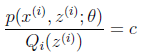
，进一步变换：将Qi(z)乘到右边，并且对Z求和，因为我们有，所以很容易得到：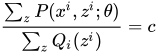
，进一步有
，则进一步可以得到：
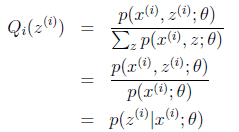
这个式子代表了什么意思呢？ 我认为它告诉我们，我们拿不定的隐藏变量的某种概率分布，其实就是参数固定时已知观测样本对隐藏变量的后验概率分布，到目前为止，我们确定了当参数θ固定时，如何选择隐藏变量的概率分布问题，其实已经完成了EM算法的E步这个过程，接下来所谓的M步 就是固定住我们求得的Qi(z)，将θ看作是自变量，对θ进行求导，求出在当前可行域范围内的极大值解θ'，然后重新固定住θ'，继续寻找新的Qi(z)，如此反复的迭代下去，便可以找到最优值！
EM算法：
1 e-step: 求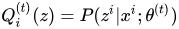 
2 m-step: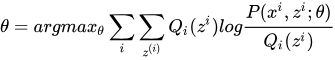 
别忘了我们其实一直操作的是极大似然函数的下界，也就是说我们是通过不断的提升似然函数的下界，从而逼迫似然函数不断的提升最后得到最大值的，即所谓的极大似然函数！从而进一步可以得到参数值。
如此重复进行下去，便可以得到极大值解，从而求出最优的参数θ！ ，整个过程可以用图像很直观的表示出来：
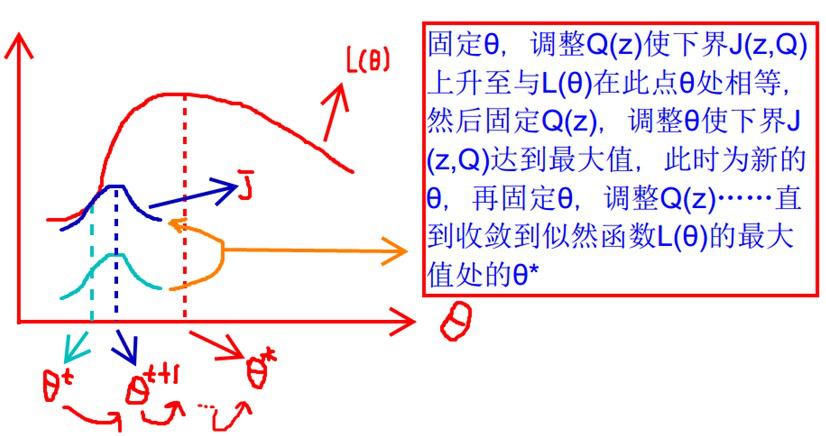
没错，虽然原作者这个图画得确实不美观，但是不得不说这个图确实是非常清晰的将整个EM算法的过程描绘了出来，一看就懂，神作！，从浅蓝色的线到深蓝色的线其实就是完成了Qi(z)值的不断探索确定的过程，最终得到下界逼近似然函数的结果是后验概率，(实际上这里完成了E-step的操作)。然后很明显深蓝色的线条的最大值并不是相交的点，于是就将Qi(z)的值固定住，对θ的结果求导，进一步得到极大值点也就是θ t+1这个位置，后续会继续从θ t+1接着上探，然后再相交，然后再固定住Q,继续对θ求极大值，这样不断的上探，变化，循环下去，就完成了对似然函数的下界的极大化的操作，这也就是整个EM算法的核心思想！
最后要讨论的是EM算法如何保证收敛性的问题：
仔细回想博文中所讲，我们要证明的是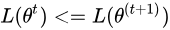 
，也就是说随着EM算法的进行，似然估计需要不断增大，单调递增才能够保证我们最后寻找到的参数是极大似然估计对应的参数不是吗，那么我们该如何证明呢？
不妨假设迭代过程已经进行了到了t时间，而且我们的θt已经给定，（实际上就是说t时间迭代的EM算法已经完成了对应的E-step，），那么此时的似然函数的公式便是：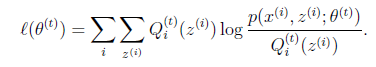
，
我们直接给出结论公式并加以解释：
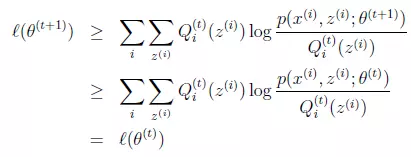
1 上式第一个大于等于号成立的原因是因为当前我们处在t时间的E-step，如果将此时的Q固定住，对θ求导数，得到了局部最大值θt+1,那么，按照EM算法的迭代逻辑，接下来就要进入t+1时间段的E-step，就是利用当前的θt+1，继续求t+1时刻的Q的最大值，只有求出了Q对应的最大值，我们才可以说下界函数在这个点上和似然函数是相等的，否则下界函数一定是小于等于似然函数的，这也就是第一个大于等于号成立的原因，通俗的说就是t时刻的M-step上，尽管参数来到了θt+1，但是此时没有进行下一个时间段t+1的E-step，所以下界函数小于等于似然函数是恒成立的！
2 第二个大于等于号成立的原因是，因为我们是在t时刻求导得到的局部极大值点θt+1，所以θt+1对应的下界函数值一定是大于等于θ时刻的下界函数值的，求导寻找极大值点自然得到的值要大于寻找之前的不是吗！
两个大于等于号都解释通了之后，我们就得到了最终我们要证明的结论，即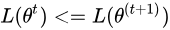！是不是很简单呐！
等一哈，可能会有同学问网上这么多博客和教学视频里面讲的EM算法包括我自己写的这篇为什么和李航老师的《统计学习方法》差别这么大啊？有什么联系？到底我该学习哪个呢？
一开始我也是看不太懂李航老师的方法，我概率论是该复习一下了，然后参考网上的博客发现，我勒个去，完全不一样啊，这怎么学！为了不误人子弟，我查阅不少博主的博文和李航老师的书对比着看，再结合第二篇博主的思路，终于弄明白一点。PS:第二篇博主的描述总让我读不懂，所以我再重新组织一下写出来：
李航老师在书中提到的EM算法如下：
1 选择参数的初值θ(0),开始迭代
2 E步： 记θ(i)为第i次迭代参数θ的估计值，在第i+1次迭代的E步，计算：,大名鼎鼎的Q函数，这里
是在给定观测数据Y和当前的参数估计θ(i)下隐变量数据Z的条件概率分布。
3 M步： 求使得 极大化的θ，确定第i+1次迭代的参数的估计值θ(i+1)
4 重复第2步和第3步，直到收敛为止
以上就是书本中李航老师的关于EM算法的定义，那么它和我们的博客中写的EM 算法具体有什么关系呢？
先直接给出结论，实际上所谓的 Q函数其实就是我们博客当中所说的似然函数的下界！
证明：
首先，我们的目的是极大化观测数据关于参数θ的似然函数，必然是希望当θ取新的值的时候，似然函数的值会变大，那么假设我们已经有了参数θ(i)而且希望新的参数θ对应的L(θ)会比旧的似然函数更大！那么我们对两者取差值：
(这里使用了Jason 不等式进行变化)
然后我们令
很明显这个就是L(θ)的一个下界！这里大家应该都能看得到懂～
那么如果我们优化这个下界，就可以迫使似然函数值不断的增加！因此，我们需要在下界函数里找能够使得下界不断提升的θ，达到我们的目的！
那么，上述公式里面凡是和θ无关的不影响优化的常量都可以去掉！我们来划简一下：
(自变量是关于θ的一个优化过程)
（这里L(θ(i+1)）和后面log里面分母都是关于θ(i)的，可以直接去掉
是不是突然发现，划简到这一步豁然开朗啊，原来这里的关于θ的最大值的里面的部分其实就是李航老师书中所说的Q函数
综上所述，李航老师让我们求出Q函数，其实就是在Qi(z)确定的情况下求出函数的最优下界，和我们之前博文中所讲的是一模一样的！
可能还会有较真的同学说 我怎么知道你这个下界和他的下界是不是一个下界啊！ 那没办法了，只能比较一下了。。。。
我们博客中E-step进行完所得到的下界：
博客中所得到的下界：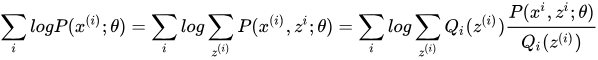
李航老师的书中所得到的下界：
我们先将无关量L(θ(i+1)）去掉，然后发现 可不是嘛，太巧了，log后面那个分式的分母不就是前面博文中我们假设的隐含变量的那个某种分布的极大值嘛---进一步说这里就是后验概率分布！
剥掉它的外衣之后你会发现呀，原来两个看起来不同的思路原来是在做同样的事情啊！奇妙奇妙真奇妙！ 写完啦～～
参考博客：
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
https://www.jianshu.com/p/c8ac8cd5471b
写的都挺好，十分感谢，要是读我的看得似懂非懂，建议阅读上述两个更经典的博文！