题目描述:
/**
* 给定一棵二叉搜索树,请找出其中的第k小的结点。
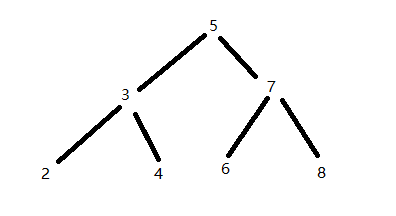
* 例如, (5,3,7,2,4,6,8)中,
* 按结点数值大小顺序第三小结点的值为4。
* 这是层序遍历:
* 5
* 3 7
* 2 4 6 8
思路:
二叉搜索树的中序遍历(左--中--右)就是按照从小到大进行排好序的结果,所以如果你想输出第k小的节点就是找到从左到右的第k个数就ok了!
所以这个问题可以转化为求二叉搜索树的中序遍历的方法!
递归版:
public TreeNode kthNode2(TreeNode pRoot,int k) { if(pRoot==null||k==0) return null; inorder(pRoot,k); return root; } private void inorder(TreeNode pRoot, int k) { if(pRoot==null) return; inorder(pRoot.left,k); //返回完了之后就对应着倒数第一个节点! cnt++; if(cnt==k) root = pRoot; inorder(pRoot.right,k); }
递归版代码解释:
其实思路很简单,但是需要人为的去在脑子里过一遍,因为是二叉搜索树,所以最最最左边的节点,一定是最小的,因此我们需要直接走到整棵树的最左边的节点,也就是2!用递归的方法如何实现呢?
inorder(pRoot.left,k); + (if(pRoot==null) return;) 两个神器搭配就可以直接走到整棵树的最左边的节点!然后接下来的任务就有意思了,进到最左边的节点之后,它一定是最小的,所以我们让全局变量cnt++;也就是说它代表了倒数第一小的节点!之后是一个if判断,if(cnt==k),root=pRoot;如果相等了代表当前节点就是你要找的节点,直接给TreeNode root赋值就可以结束,否则的话,继续进到它的右节点进行寻找!为什么这里要进右节点呢?
考虑第一次返回,说明2节点的左子树肯定为null,那么根据中序遍历 左--->中---->右的原则,你找完了中间节点,必须去到它的右子树里看看是否存在右子树!如果右子树存在,那么继续一路飙到最左边,然后count++!这才代表了倒数第二个节点的存在!当你的右子树找完之后,自然函数会返回,那么它返回的一定是上一层的中间节点3!此时依然要执行3这个节点的右节点!因为你返回上去之后,它一定是上一层的树的中间节点,而你刚刚进入下以层找的恰好是它的左子树!所以要继续找3的右子树!
这就是为什么每次count++;之后要找右子树再进入递归的原因!因为你在递归进左子树的过程中你实际上进入的是(1 子树结构的左节点,2 “根”结构的中间节点)
所以,你一旦返回就证明着你现在位于高层次树的中间节点上,接下来等着你处理的一定是右子树!!!
以上是我对递归法中序遍历二叉搜索树的一些理解!
非递归实现:
1 if(pRoot==null|| k==0) 2 return null; 3 int count=0; 4 Stack<TreeNode> stack = new Stack<>(); 5 while(pRoot!=null || !stack.isEmpty()) 6 { 7 8 while(pRoot!=null) 9 { 10 stack.push(pRoot); 11 pRoot = pRoot.left; 12 } 13 pRoot = stack.pop();//倒数第一小的节点出来了! 14 count++; 15 if(count==k) 16 return pRoot; 17 pRoot = pRoot.right; 18 } 19 return null;
现在我觉得迭代的实现其实就是把原来递归隐式使用计算机栈的规则给显式的表示出来!
新建一个栈,while(pRoot!=null || !stack.isEmpty())
当pRoot没走到最后或者栈里面还有元素的时候我们就在这个循环里面继续进行
继续判断如果是pRoot!=null那么二话不说直接压栈到最左边的节点一样的操作!
从栈里面弹出一个节点,此时的节点就是最左边的最小值,然后count++;
后面的代码和递归版基本一致!判断等不等于k,然后继续!最关键的是最后的一行代码,pRoot = pRoot.right;
我们仍旧需要进入到它的右子树里面重复执行,此时我们会看这个条件!while(pRoot!=null||!stack.isEmpty())
它其实就是代表的两种情况 :
1 右子树存在,那么继续压栈处理走到最左边慢慢往上升
2 右子树不存在程序返回,那么此时栈就必须存在树节点,而此时的树节点就刚好是上层的中间节点了!
所以一个非常重要的思想是:
节点在子树里面充当的是左节点!一旦它上升到上一层树的级别,那么在这个结构里面它就是中间节点,所以必须往右子树里继续执行!