在此之前,针对APS写了一些理论性的文章;而对于Optaplanner也写了一些介绍性质,几少量入门级的帮助初学者走近Optaplanner。在此以后,老农将会按照Optaplanner官方的用户手册的结构,按章节地对其进行翻译,并成型一系列的操作说明文章。在文章中,为了降低对原文的理解难度,有些地方我不会直接按原文档的字面翻译,而是有可能加入一些我自己的理解,或添一些解释性的内容。毕竟英语环境下的思维和语言表达方式,跟中文或多或少会有差别的,所以如果全部按字面翻译,内容就非常生硬,可读性差,解程难度较大。我认为应该在理解了作者原意的基础上,再进一步以中文方式的表达,才算是真的的本地化。记得老农还是少农时,学习开发技术,需要阅读一些外国书箱的翻译本时,印象最深的是候捷老师的书,尽管《深入浅出MFC》,砖头厚度的书,硬是被我翻散了线,MFC尽管真的晦涩难懂,但候老却能把Windows的消息机制及MFC中整个个宏体系,系统地通俗地描述出来,令读者不需要花费太多精力去理解猜测书中字面的意义,大大降低的VC++中MFC的学习门槛。但老农毕竟只是一个一线开发人员,不是专业的技术资料翻译人才,不可能有候老师的专业水平,因此,我也只可尽我所能把内容尽量描述得通俗一些,让读者尽量容易理解,花费更少的时间掌握这些知道要点。
本文以Optaplanner 7.10.0 Final版本的开发手册作为基础进行翻译。
1. Optapplanner 介绍
1.1. 什么是Optaplanner?
每个组织都需要面对规划、排程问题:在有限的资源约束下提供服务与产品(例如人员,资产,时间及资本等限制)。Optaplanner可以优化这类规划、排程问题,令到使用它的组织可以用更少的资源做更多的事(尽可能的花少钱办大事)。这就是著名的的约束满足规划,它属于运筹学的一部分。
Optaplanner是一个轻量的、可嵌入的,可以对规划问题进行优化的约束满足引擎,它可以解决案例有:
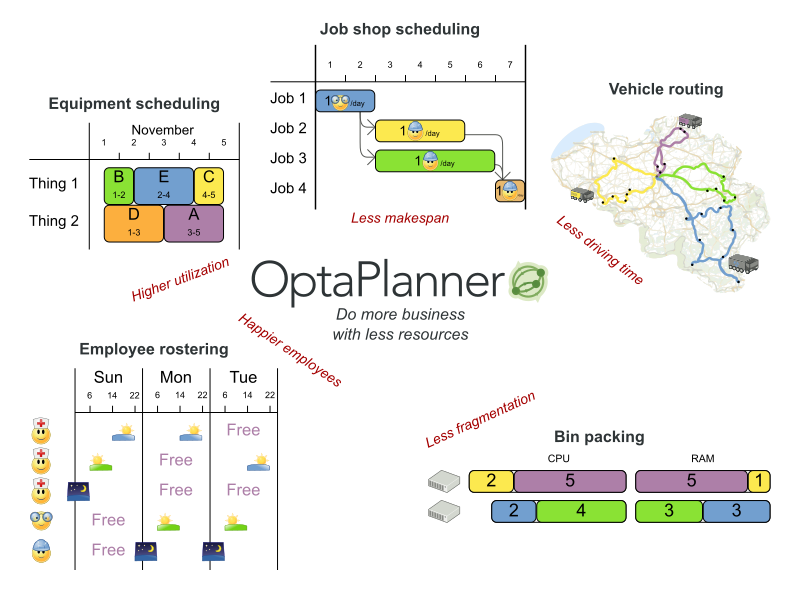
- 员工排班:为护士、维修工等人员制定上班时间表。
- 方程安排:安排会议、约见、维修工作、广告时间等。
- 教育领域的时间安排:安排课程、课堂、考试、会议讲座等。
- 规划车辆运动路线:通过已知的地图工具,为货运、客运(货车、火车、轮船、航班等)规划交通工具多目标的运行路线。
- 装箱问题:向容器、货车、轮船和仓库装载货物,同时可以规划电脑的资源加载利用,例如云计算的资源分配问题。
- 车间生产安排:规划汽车组装生产线,机器队规划,劳动任务的规则等。
- 下料问题:在下料分割的时候,实量最小的浪费,例如切割纸张、钢铁、地毯等。
- 运动赛事安排:规划比赛和训练,例如安排足球联赛、棒球联赛等。
- 金融优化:投资组合优化、实现风险分散等。
1.2. 什么是规划问题?
一个规划问题,基于有限的资源和指定的约束,有一个优化目标。优化目标可以是多种事物,例如:
- 利润最大化 - 优化目标得出的结果是尽可以高的利润。
- 最小化生态足迹(即尽可能减少对生态的影响) - 优化目标是对环境产生尽可能小的影响。
- 最大化员工或客户的满足度 - 优化目标重视员工与客户的需要。
实现这些目标的能力依赖于可用资料的数量,例如:
- 人员数量
- 时间
- 预算
- 特殊资产,例如机台,车辆,计算机,建筑物等。
与这此资源相关的约束也必然计算在内,例如,一个人的工作小时数, 他们可使用(操作)的机台数量,设备之间的兼容性等。
Optaplanner可以帮助Java程序员有效地解决约束满足问题, 在Optaplanner引擎中,对每个有效的约束分数计算中,组合了启发式和元启发式算法。
1.2.1 规划问题属于NP-Complete问题或NP-hard问题
上述所有的案例或许都属于NP-complete/NP-hard问题,(什么是NP-Complete/NP-hard问题呢?),在外行人看来,它的定义是:
对于一个问题:
- 在合理时间内可以容易地验证一个给定的解。
- 在合理时间内,目前尚没有行之有效的解法,能找到其绝对最优解(注1)。
(注1):至少,到目前为止,仍未有一个世界上最聪明的计算机科学家能找到此方法。可是一旦他们找到对其中一个NP-Complete问题的有效解法,那么这个方法对所有NP-Complete问题都是可行办法。事实上,如果任何人只需证明是这种解法的存在与否,即可获得100万美元的奖励。
其实这其含义是相当悲观的:要解决这些问题或许比你预想中更困难,因为目前针对这种问题的常见两种技术是未足够解决此类问题的。这两种方法是:
- 暴力算法(尽管是一些优化过,相对聪明的暴力算法变种), 但获得其解所需的时间非常长(译者:主要原因是时间复杂度非常高)。
- 快速算法,例如在Bin packing问题中,先装入最大项;但得到的解离绝对最优解仍存在相当大距离的。
通过使用一些更高级的算法,Optaplanner可以在合理的时间内,对这些规划问题找到相对较优解。
1.2.2 规划问题存在约束(包括硬约束与软件约束)
通常来说,一个规划问题至少包括两个层次的约束:
- (负面)硬约束,不可被违反。例如:一个教师在同节的时间内不能同时上两门课。
- (负面)软件约束,若可避免,它不应该被违反。例如:教师都不太喜欢在周五下午上课。
也有些问题存在一些正面的约束:
- 正面分数在可能情况下应该实现。例如:教师B喜欢在周一上午上果。
一些比较基础的规划问题(例如8王后问题),只存在硬约束;有一些规划问题则存在超3层,甚至更多层次的约束。例如:硬约束,中间约束和软约束。
这些约束会被定义在规划问题的Score calculation里(也称为适应度函数)里。规划问题里的每一个解的优劣,都可以通过分数来评价。在Optaplanner中,分数约束是通过面向对象语文编写的,例如Java代码或通过Drools脚本实现的rules. 这些代码相当容易编写,灵活且易于扩展。
1.2.3 规划问题存在巨大的搜索空间
一个规划问题存在非常多的解,这些解可以分为以下数种:
- 可能解:规划问题的任意一个解都称作可能解,无论这个解是否违反了约束,或违反了多少约束。规划问题往往存在令人难以至今的巨量可能解,这里面很多解是毫无价值的。
- 可行解:规划问题的可行解是指没有违反任何(负面)硬约束的解。一个规划问题的可行解的数量,与其可能解相关。有时也不存在可行解,一个规划问题的每一个可行解,都是该问题的一个可能解。
- 绝对最优解:绝对最优解是这个规则问题获得约束分最高的那个解。规划问题通常只有1个或少量数个绝对最优解。通常存在至少1个绝对最优解,尽管当这个规划问题不存在可行解,它也存在绝对最优解,这时候绝对最优解就是非可行解。
- 相对最优解:相对最优解是指规划问题在一定的求解时间内得到评分最高的解。相对最优解通常是可行解,只要有足够的运行时间,找到的相对最优解就是绝对最优。
此外,尽管基于一个较小的数据集描述的一个规划问题,其可能解的数量通常是非常巨大的(如果计算正确的话)。正如你从示例中可以看到,大多数情况下,一个规划问题的可能解数量,对目前已知宇宙的原子数量还要多(10的80次方)。因为目前还没有直接的办法找出规划问题的绝对最优解,一些求解实现方法是通过暴力穷举的方法,至少可以穷举所有可能解中的一个子集。
OptaPlanner支持多种优化算法,以有效地涉足大量可能解,根据不同使用场景的情况,一些优化算法的性能比其它算法更佳,但哪个更佳是无法预先告知的(译者:需要通过Benchmark等功能测定)。在Optaplanner里,很容易能过修改几行XML内容或Java code,来更改求解器的配置,从而切换不同的优化算法。
【未完,待续...】
原创不易,如果觉得文章对你有帮助,欢迎点赞、评论。文章有疏漏之处,欢迎批评指正。
本系列文章在公众号不定时连载,请关注公众号(让APS成为可能)及时接收,二维码:

如需了解更多关于Optaplanner的应用,请发电邮致:kentbill@gmail.com
或到讨论组发表你的意见:https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信(13631823503)或QQ(12977379)实时沟通,但因本人日常工作繁忙,通过微信,QQ等工具可能无法深入沟通,较复杂的问题,建议以邮件或讨论组方式提出。(讨论组属于google邮件列表,国内网络可能较难访问,需自行解决)
