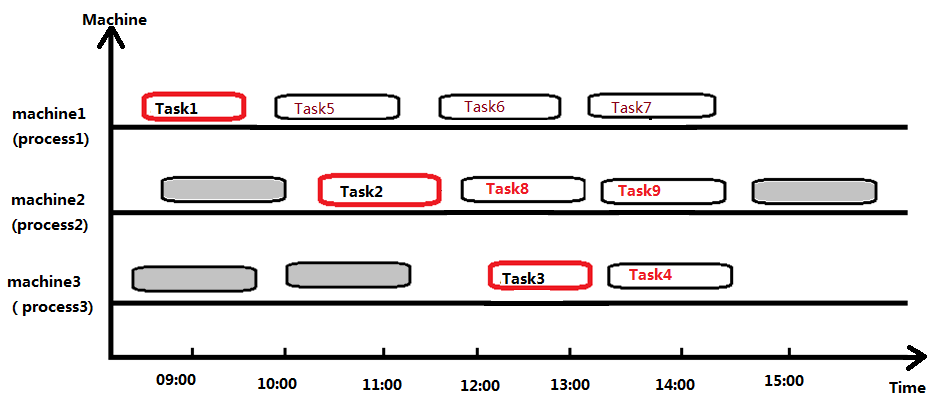
时间槽模式 - Time slot
-
规划实体中的规划变量是一个时间区间;
-
一个规划变量的取值最多仅可分配一个时间区间;
-
规划变量对应的时间区间是等长的。
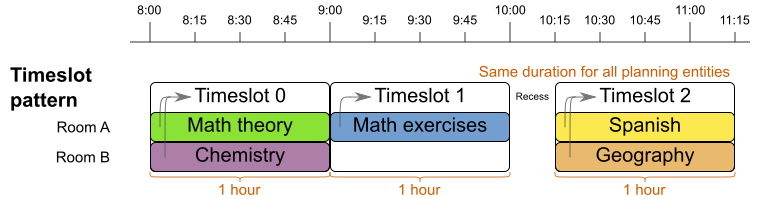
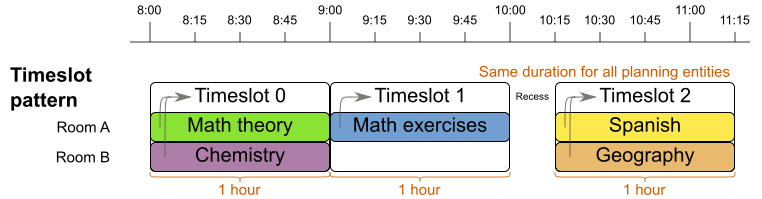
从图中可以看出,每门课所需的时间都是固定一小时。具体到这个模式的应用,因为其原理、结构和实现起来都相当简单,本文不通过示例详细讲解了。可参考示例包中的Course timetabling中的设计和代码。
时间粒模式 - Time Grain
-
规划变量是时间区间;
-
业务上对应于规划变量的时间区间可以不等长,但必须是Grain的倍数。
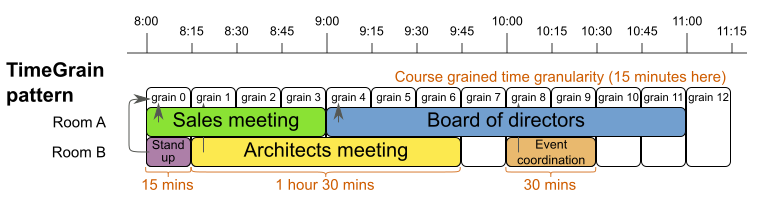
从上图可以看到,每个会议所需的时间长度是不相等的,但是其长度必然是一个Time Grain的倍数,从图中上方的时间刻度可以比划出一个TimeGrain应该是15分钟。例如Sales meeting占用了4个Time Grain,即时长1小时。Time Grain模式的使用会相对Time Slot更灵活,适用范围会更广。通过设置可知,其实适用于Time Slot模型的情形,是完全可以通过TimeGrain模式实现的,只是实现起来会更复杂一些。那么Time Grain模式的设计要点在哪里呢?要了解其设计原理,就得先掌握Time Grain的结构及其对时间的提供方法。
-
设计好每个Grain的粒度,也就是时间长度。并不是粒度越细越好,例如以1秒钟作为一个粒度,是不是就可以将任务的时间精度控制在1级呢?理论上是可以的,但日常使用中不太可行。因为这样的设计会产生过量的Grain,Grain就是Value Range,当可选值的数量过多时,整个规划问题的规模就会增大,其时间复杂度就会指数级上升,从而令优化效果降低。
-
定义好每个Grain与绝对时间的映射关系。这个模式中的Time Grain其时间上是相对的。如何理解呢?就是说,这个模式在运行的时候,会把初始化出来的Grain对象列表,以Index(Grain的序号)为序形成一个连接的时间粒的序列。列表中每一个具体的Grain对应的绝对时间是什么时候呢?是以第一个Grain作为参照推算出来的。例如上图中的第一个Grain - grain0它的起始时间是8:00, 那么第6个grain - grain5的起始时间就是9:30,这个时间是通过grain0加上6个grain的时长推算出来的,也就是8:00加上1.5小时,因此得到的是9:30。因此,当你设定Time Grain与绝对时间的对应关系时,就需要从业务上考虑,grain0的起始是什么时刻;它决定了后续所有任务的时间。
public int calculateOverlap(MeetingAssignment other) { if (startingTimeGrain == null || other.getStartingTimeGrain() == null) { return 0; }
int start = startingTimeGrain.getGrainIndex(); int end = start + meeting.getDurationInGrains(); int otherStart = other.startingTimeGrain.getGrainIndex(); int otherEnd = otherStart + other.meeting.getDurationInGrains(); if (end < otherStart) { return 0; } else if (otherEnd < start) { return 0; } return Math.min(end, otherEnd) - Math.max(start, otherStart); }
时间链模式 - Chained Through Time
Chained Through Time模式的意义

Chained Through Time的内存模型
-
一条链由一个Anchor(锚),和零或,或1个,或多个Entity(实体,其实就是规划实体)构成;
-
一条链必须有且仅有一个Anchor(锚);
-
一条链中的Entity或Anchor之间是一对一的关系,不可出现合流或分流结构;
-
一条链中的Entity或Anchor不可出现循环。
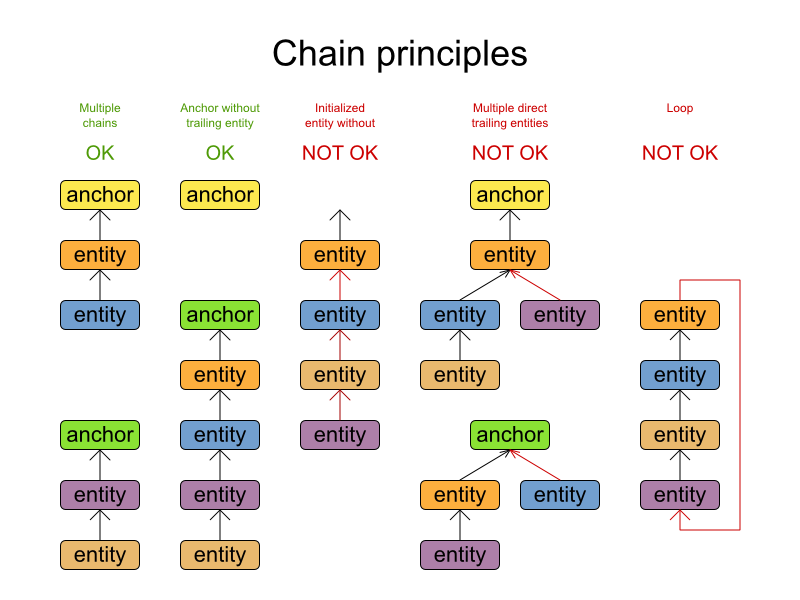
Chained Through Time模式的设计实现
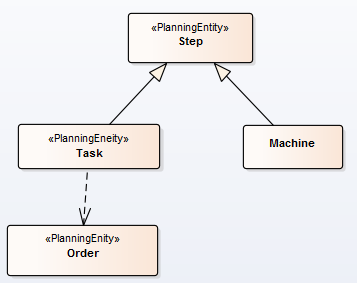
时间推算方法
Chained Through Time模式与其两种时间规划模式不同,本质上它并不对时间进行规划,只对实体之间的关系进行规划优化。因此,在引擎每一个原子操作中需要通过对VariableListener接口的实现,来对时间进行推算,并在完成推算后,由引擎通过评分机制进行约束评分。一个Move有可能对应多个原子操作,一个Move的操作种类,可以参见开发 手册中关于Move Selector一章,在以后对引擎行为进行深入分析的文章中,我将会写一篇关于Move Seletor的文件,来揭示引擎的运行原理。在需要进行时间推算时,可以通过实现接口的afterVariableChanged方法,对当前所处理的规划实体的时间进行更新。因为Chained Through Timea模式下,所有已初始化的规划实体都处在一条链上;因此,当一个规划实体的时间被更新后,跟随着它的后一个规划实体的时间也需要被更新,如此类推,直到链上最后一个实体,或出现一个时间正好不需要更新的规划实体,即该规划实体前面的所有实体的时间出现更新后,其时间不用变化,那么链上从它往后的规划实体的时候也无需更新。
以下是VariableListener接口的afterVariableChanged及其处理方法。
// 实现VariableListener的类 public class StartTimeUpdatingVariableListener implements VariableListener<Task> { // 实现afterVariableChanged方法 @Override public void afterVariableChanged(ScoreDirector scoreDirector, Task task) { updateStartTime(scoreDirector, task); } @Override public void beforeEntityAdded(ScoreDirector scoreDirector, Task task) { // Do nothing } @Override public void afterEntityAdded(ScoreDirector scoreDirector, Task task) { updateStartTime(scoreDirector, task); } . . . }
//当一个任务的时候被更新时,顺着链将它后面所有任务的时候都更新 protected void updateStartTime(ScoreDirector scoreDirector, Task sourceTask) { Step previous = sourceTask.getPreviousStep(); Task shadowTask = sourceTask; Integer previousEndTime = (previous == null ? null : previous.getEndTime()); Integer startTime = calculateStartTime(shadowTask, previousEndTime); while (shadowTask != null && !Objects.equals(shadowTask.getStartTime(), startTime)) { scoreDirector.beforeVariableChanged(shadowTask, "startTime"); shadowTask.setStartTime(startTime); scoreDirector.afterVariableChanged(shadowTask, "startTime"); previousEndTime = shadowTask.getEndTime(); shadowTask = shadowTask.getNextTask(); startTime = calculateStartTime(shadowTask, previousEndTime); } }
规划实体的设计
上一步我们介绍了如何通过链在引擎的运行过程中进行时间推算,那么如何设定才能让引擎可以执行VariableListener中的方法呢,这就需要在规划实体的设计过程中,反映出Chained Through Time的特性了。我们以上面的类图为例,理解下面其设计要求,在此示例中,把Task作为规划实体(Planning Entity), 那么在Task类中需要定义一个Planning Variable(genuine planning variable), 它的类型是Step,它表示当前Task的上一个步骤(可能是另一个Task,也可能是一Machine). 此外,在 @PlanningVariable注解中,添加graphType = PlanningVariableGraphType.CHAINED说明。如下代码:
// Planning variables: changes during planning, between score calculations. @PlanningVariable(valueRangeProviderRefs = {"machineRange", "taskRange"}, graphType = PlanningVariableGraphType.CHAINED) private Step previousStep;
以上代码说明,规划实体(Task)的genuine planning variable名为previousStep, 它的Value Range有两个来源,分别是机台列表(machineRange)和任务列表(taskRange),并且添加了属性grapType=planningVariableGraphType.CHAINED, 表明将应用Chained Through Time模式运行。
有了genuine planning variable, 还需要Shadow variable, 所谓的Shadow variable,在Chained Through Time模式下有两种作用,分别是:
1. 用于建立两个对象(Entity或Anchor)之间的双向依赖关系;即示例中的Machine与Task, 相邻的两个Task。
2. 用于指定当genuine planning variable的值在规划运算过程产生变化时,需要更改哪个变量;即上面提到的开始时间。
,对于第一个作用,其代码体现如下,在规划实体(Task)中,以@AnchorShadowVariable注解,并在该注解的sourceVariableName中指定该Shadow Variable在链上的前一个对象指向的是哪个变量。
// Shadow variables // Task nextTask inherited from superclass @AnchorShadowVariable(sourceVariableName = "previousStep") private Machine machine;
上述代码说明成员machine是一个Anchor Shadow Variable, 在链上,它连接的前一个实体是实体类的一个成员 - previousStep.
Chained Through Time中的链需要形成双向关系(bi-directional),下图是路线规划示例中。一个客户与上一个停靠点之间的双向关系。
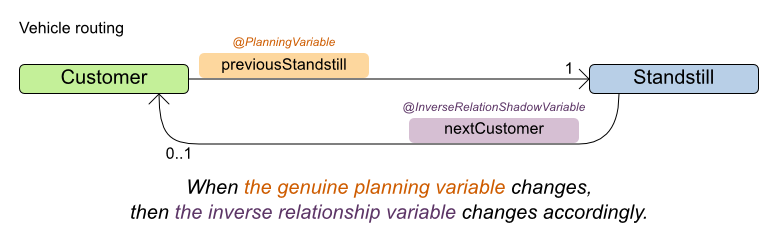
在规划实体(Task)中我们已经定义了前一个Step,并以@AnchorShadowVariable注解标识。而双向关系中的另一方,则需要在相邻节点中的前一个节点定义。通过链的内存模型,我们可以知道,在生产计划示例中,一个实体的前一个节点的类型可能是另一个Task, 也要能是一个Machine, 因此,前一个节点指向后一个节点的规划变量,只能在Task与Machine的共同父类中定义,也就是需要在Step中实现。因此,在Step类中需要定义另一个Shadow Variable, 因为相对于Task中的Anchor Shadow variable, 它是反现的,因此,它需要通过@InverseRelationShadowVariable注解,说明它在链上起到反向连接作用,即它是指向后一个节点的。代码如下:
@PlanningEntity public abstract class Step{ // Shadow variables @InverseRelationShadowVariable(sourceVariableName = "previousStep") protected Task nextTask; . . . }
可以从代码中看到,Step类也是一个规划实体.其中的一个成员nextTask, 它的类型是Task,它表示在链中指向后面的Entity. 大家可以想一下,为什么它可以是一个Task, 而无需是一个Step。
通过上述设计,已经实现了Chained Through Time的基本模式,可能大家还会问,上面我们实现了VariableListener, 引擎是如何触发它的呢。这就需要用到另外一种Shadow Variable了,这种Shadow Varible是用于实现在运算过程中执行额外处理的,因此称为Custom Shadow Variable.
// 自定义Shadow Variable, 它表示当 genuine被引擎改变时,需要处理哪个变量。 @CustomShadowVariable(variableListenerClass = StartTimeUpdatingVariableListener.class, sources = {@PlanningVariableReference(variableName = "previousStep")}) private Integer startTime; // 因为时间在规划过程中以相对值进行运算,因此以整数表示。
上面的代码通过@CustomShadowVariable注解,说明了Task的成员startTime是一个自定义的Shadow Variable. 同时在注解中添加了variableListenerClass属性,其值指定为刚才我们定义的,实现了VariableListener接口的类 - StartTimeUpdatingVariableListener,同时,能冠军sources属性指定,当前Custom Shadow Variable是跟随着genuine variable - previousStep的变化而变化的。
至此,关于Chained Through Time中的关键要点已全部设计实现,具体的使用可以参照示例包中有用到此模式的代码。
总结
关于时间的规划,在实际的系统开发时,并不只本文描述的那么简单,关于最为复杂的Chained Through Time模式,大家可以通过本文了解其概念、结构和要点,再结合示例包中的代码进来理解,才能掌握其要领。且现实项目中也有许许多多的个性规则和要求,需要通过大家的技巧来实现;但万变不离其宗,所有处理特殊情况的技巧,都需要甚至Optaplanner这些既有特性。因此,大家可以先通过示例包中的代码将这些特性掌握,再进行更复杂情况下的设计开如。未来若时间允许,我将分享我在项目中遇到的一些特殊,甚至是苛刻的规则要求,及其处理办法。
如需了解更多关于Optaplanner的应用,请发电邮致:kentbill@gmail.com
或到讨论组发表你的意见:https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信(13631823503)或QQ(12977379)实时沟通,但因本人日常工作繁忙,通过微信,QQ等工具可能无法深入沟通,较复杂的问题,建议以邮件或讨论组方式提出。(讨论组属于google邮件列表,国内网络可能较难访问,需自行解决)