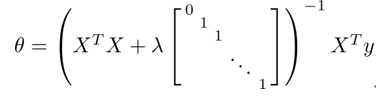一、 Logistic回归与Logistic函数
分类问题的标签可以是$yepsilon left { 0,1 ight },yepsilon left { 0,1,2 ight },yepsilon left { 0,1,2,3,... ight }$,对应分别为二元、三元、…分类问题。借鉴线性回归算法,我们希望预测样本属于每个标签的概率$pleft { y=i ight }$ ,而且$pepsilon left [ 0,1 ight ]$。将概率最大的标签作为分类结果。这里的概率就对应为假设函数$h_ heta (x)$,与线性回归不同,logistic回归要求$h_ heta (x)epsilon left lfloor 0,1 ight floor$。于是新的$h_ heta (x)$函数的构造如下:
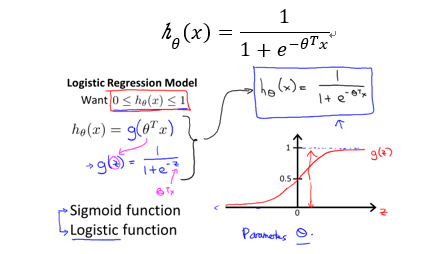
二、 Logistic决策边界(decision boundary)
以二元分类为例,从假设函数中可以发现,当$ heta^Tx>0$时,概率大于0.5,因此预测y=1;反之预测y=0。$ heta^Tx=0$就是决策边界,其展开形式为:$ heta_0x+ heta_1x+ heta_2x+...=0$。对应的边界线如下图所示:
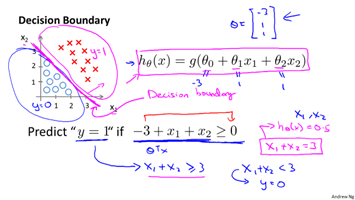
这里的边界就是一条直线,将空间划分为两个区域。如果是多项式回归,那么边界可能是下面形式:

三、 Logistic代价函数
以二元分类为例,Logistic回归同线性回归一样,都要确定合适的模型参数,来更好地预测概率。同样,使用代价函数来评价$ heta$好坏,logistic回归里采用对数代价形式:
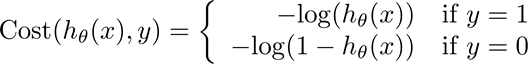
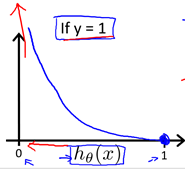
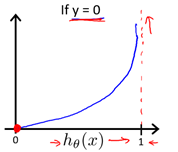
当所给标签为1时,如果预测的概率接近1,则代价接近0;如果预测的概率接近0,则代价接近无穷。当所给标签为0时,如果预测的概率接近1,则代价接近无穷;如果预测的概率接近0,则代价接近1。
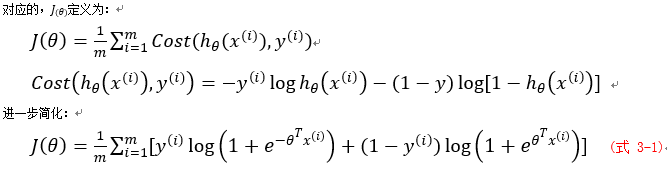
四、 Logistic梯度下降
用代价函数去惩罚模型参数:
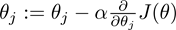
对式3-1求偏导可得:

五、 多分类问题
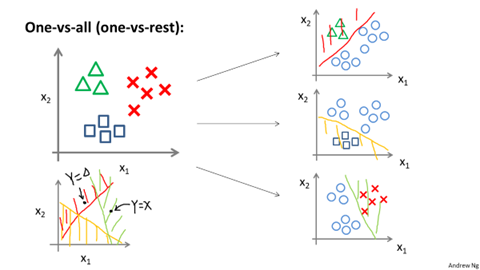
解决多分类的一种思想是分解为多个二分类,为每一个二分类都维护一个假设函数,记成下面的形式:

例如三分类中,我们维护三个假设函数:$h_ heta^{(0)}(x)、h_ heta^{(1)}(x)、h_ heta^{(2)}(x)$,表示属于三个类的概率,当更新$h_ heta^{(0)}(x)$时,将标签为0的视作0,将标签为1、2都视作1。$h_ heta^{(1)}(x)、h_ heta^{(2)}(x)$也类似。最终预测分类的时候,比较三个假设函数值的大小,取概率最大的作为分类标准。

六、 Logistic优化算法
除了梯度下降算法,还有以下优化算法,采用优化算法,可以自动选择合适学习率,收敛更快;一般采用这些优化算法而非梯度下降,这里暂不深究算法原理与实现。
1.共轭梯度算法(conjugate gradient)
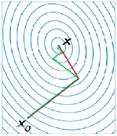
它的每一个下降方向是与上一次共轭的,其优点是所需存储量小,收敛快,稳定性高,而且不需要任何外来参数。
下图绿线为共轭梯度法。
2.拟牛顿法(BFGS)
牛顿法的突出优点是收敛很快,但是运用牛顿法需要计算二阶偏导数,而且目标函数的Hesse矩阵可能非正定。为了克服牛顿法的缺点,人们提出了拟牛顿法,它的基本思想是用不包含二阶导数的矩阵近似牛顿法中的Hesse矩阵的逆矩阵。
3.限制内存BFGS(L-BFGS)
在BFGS算法中,当优化问题规模很大时,矩阵的存储和计算将变得不可行。为了解决这个问题,就有了L-BFGS算法。L-BFGS的基本思想是只保存最近的m次迭代信息,从而大大减少数据的存储空间。
七、 过拟合(overfitting)与正则化(regularization)
1.过拟合
过拟合是指当特征量较多,或特征中有高阶项,而数据较少时,存在过分拟合的情况,与之相反的情况为欠拟合。这两种情况都对预测不利。
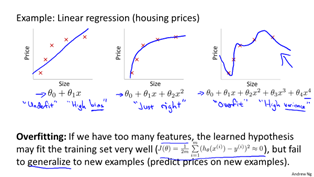
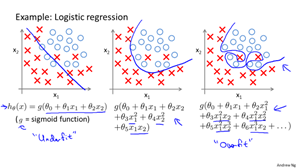
解决过拟合的办法一种是减少特征量,但会造成特征信息减少;另一种是正则化。
2.回归的正则化
对于一般地代价函数,单独地加上对参数的惩罚,如下:

这个代价函数由两部分组成:前部分是偏差,可以让函数更加贴合点,后部分可以限制参数的大小。当λ取值较大,为了最小化代价,每个参数都会趋近0,最终拟合结果就是$h_ heta(x^{(i)})=0$。如果λ适当,则既可以很好地贴合数据点,又能避免过拟合现象。
回归算法的正则化更新方程如下,对线性回归和逻辑回归都适用:
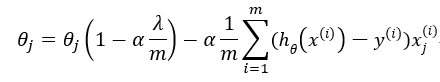
一般$1-alphafrac{lambda }{m}$的值非常接近1,例如0.98。对于正规方程的正则化公式如下,采用正则化的另一个好处是它能保证正规方程是一定可逆的。