三种方法:
1,Torch.mm(仅仅适用2维的矩阵相乘)
2,Torch.matmul
3,@
>>> a = torch.randn(3,3)
>>> b = torch.rand(3,3)
>>> a
tensor([[-0.6505, 0.0167, 2.2106],
[ 0.8962, -0.3319, -1.2871],
[-0.0106, -0.8484, 0.6174]])
>>> b
tensor([[0.3518, 0.5478, 0.9848],
[0.0434, 0.2797, 0.2140],
[0.3784, 0.8357, 0.7813]])
>>> torch.mm(a,b)
tensor([[ 0.6084, 1.4958, 1.0901],
[-0.1862, -0.6776, -0.1940],
[ 0.1931, 0.2729, 0.2904]])
>>> torch.matmul(a,b)
tensor([[ 0.6084, 1.4958, 1.0901],
[-0.1862, -0.6776, -0.1940],
[ 0.1931, 0.2729, 0.2904]])
>>> a@b
tensor([[ 0.6084, 1.4958, 1.0901],
[-0.1862, -0.6776, -0.1940],
[ 0.1931, 0.2729, 0.2904]])
#线性相乘,可以把矩阵压缩比如
>>> a = torch.rand(4,784)
>>> x = torch.rand(4,784)
>>> w = torch.rand(512,784)
>>> (x@w.t()).shape
torch.Size([4, 512])
>>> w = torch.rand(784,512)
>>> (x@w).shape
torch.Size([4, 512])
pytorch中的w=torch.rand(512=ch-out,784=ch-in)
>>> a = torch.rand(4,3,28,64)
>>> b = torch.rand(4,3,64,28)
>>> torch.mm(a,b).shape
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
RuntimeError: self must be a matrix
>>> torch.matmul(a,b).shape
torch.Size([4, 3, 28, 28])
>>> b = torch.rand(4,64,28)
>>> torch.matmul(a,b).shape
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
RuntimeError: The size of tensor a (3) must match the size of tensor b (4) at non-singleton dimension 1
>>> b = torch.rand(3,64,28)
>>> torch.matmul(a,b).shape
torch.Size([4, 3, 28, 28])
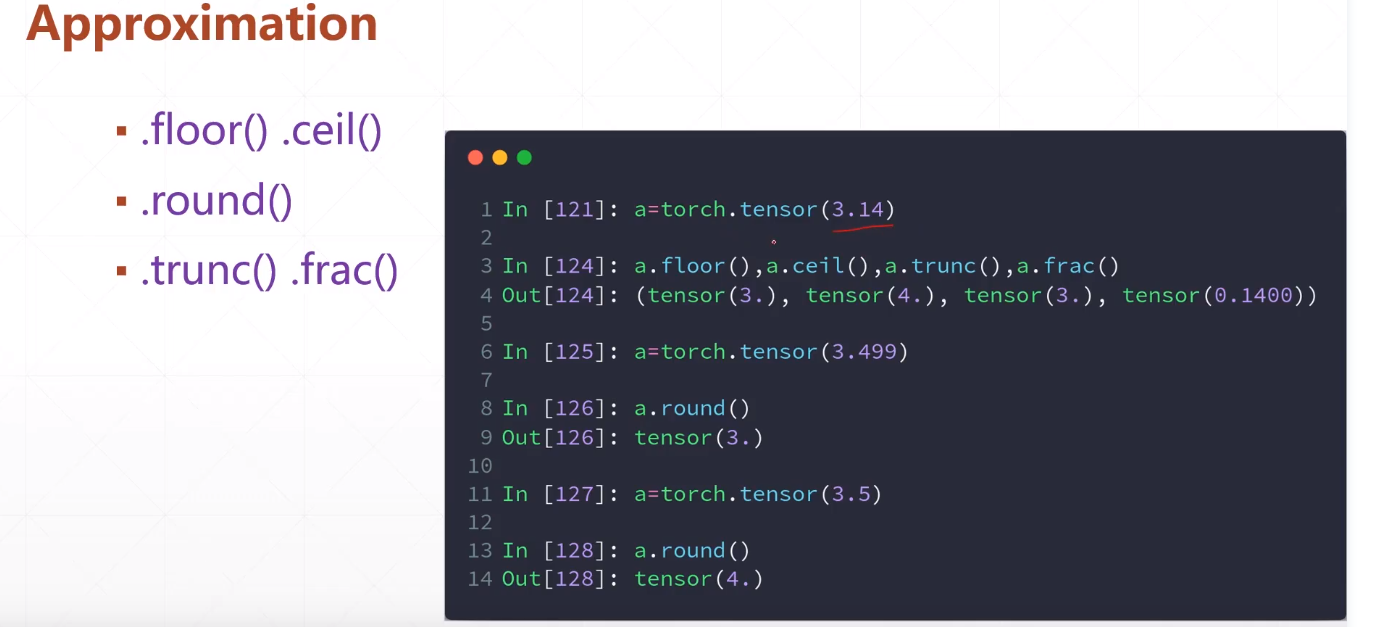
平方运算
pow(a,2/3/4次方)
a**2 平方
a.sqrt() 平方根
a.rsqrt()平方根的倒数
a**(0.5)相当于开平方

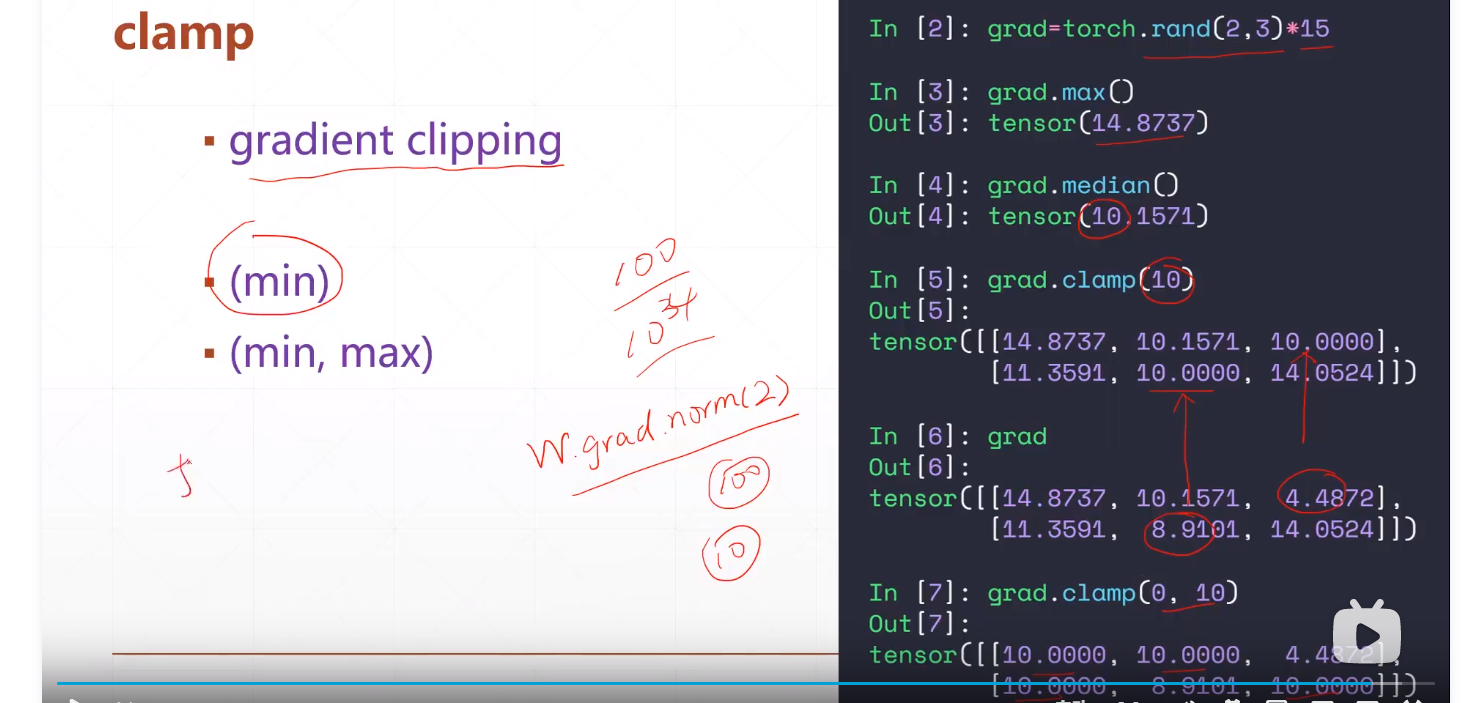
clamp可用来梯度裁剪,比如clamp(10)表示矩阵里面的数最小为10
clamp(0,10)表示矩阵里面的数都在0-10中间