引言
支持向量机在很多地方都能遇到,主要是用于分类问题,而且简单粗暴,所以也很多人用,但对其深层次原理性的探讨至始至终看到过的资料中觉得林轩田老师讲的非常地到位,另外还有一个参考资料就是v_july_v写的SVM的三重境界,但july写的太多了,可能看起来比较吃力,所以挑选了这些文档以及课程中重要的部分组成此文
本文主要是结合台大机器学习和机器学习实战这本书外加自己之前的一些学习笔记整理而得
简介
支持向量机也是一种线性分类器,与一般的线性分类器不同的是它不仅仅要把数据分开,而且想寻找最大的分类间隔
比如说对于以下的几种分类线,SVM寻找的就是D的那一条

所以综合以上两个条件:1、要能把数据分开;2、分类间隔还要最大
可以得出SVM想寻找的目标函数
目标函数

目标函数就是想基于分类正确的条件下求最大分类间隔,所以需要用到点到平面的距离
点到平面(分割面)的距离


将距离计算公式带入目标函数更新
因为yn是+1和-1,又因为yn与wx+b同号,所以绝对值可以去掉,整个问题进一步变为

很多书或者博客的讲解直接给出了标准的目标函数与条件,并没有很详细的介绍,这里我觉得台大机器学习中林轩田老师将这部分讲解的十分透彻,如何由这个本身的式子转换为标准的目标函数与条件的。
大家可以对比一下标准的SVM目标函数与条件的形式

问题:为什么之间加入了约束条件,再看看本来的约束条件,本身应该是大于0的,这里直接说约束条件是大于等于1了。这之间的过渡过程并没有讲的很清楚
将本身约束条件转变为标准问题约束条件的过程
将分类正确的条件进行变形
因为一条直线存在以下这种放缩性

所以我们只考虑直线等于1的情形,这样的话margin可以简化,台大机器学习中对这种放缩的可行性进行了分析

这样问题就可以简化,等于1了,自然大于0的条件可以舍去

我们把条件等于1放松为大于等于1,我们证明就算放松条件,最优解也会满足原条件
假设最优解落在大圈圈里
我们可以找到另外一个更优的解

然后我们把最大化问题转变为最小化问题,这个时候整个问题变为

这个问题就是标准问题
这个标准问题是一个二次规划问题,与二次规划问题的标准形式进行对比

因为二次规划问题的标准形式是寻找u,所以需要进行一些变量转换
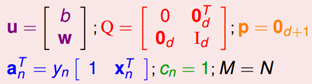
至此,把这些向量丢进一个二次规划问题求解的工具即可,得到的b,w即可算出那条分类直线
另外这种带条件优化问题的求解用的是拉格朗日乘子法,用于消除条件
拉格朗日乘子法
有N个条件,所以有N个拉格朗日乘子

可以证明拉格朗日方法虽然没有条件约束了,但是还是跟原问题等价,有很多书只是说拉格朗日乘子法可以用于解决这些问题,但并没有说为什么,以及是否跟原问题等价,这点我又一次觉得林轩田讲的问题很棒:

证明拉格朗日乘子法语原问题等价
SVM的结果是去选出一对拉格朗日乘子中最小的值,但是每一个拉格朗日乘子在大于0的条件下,调整b跟w的值使得拉格朗日方程最大。
因为如果是不满足条件的b和w,那么constraint里为正数,那么max最大化的话,因为α也是正数,会趋于无限大,最小化的时候会舍去这种情况
如果满足条件,constraint里为负数,因为α为正数,max最大化的话,α只能取0,则结果为原来的目标函数

到这里为止,所谓的hard-margin SVM也就是本身数据线性可分的情况就完全讲完了
接下来对于一些本身线性不可分的数据,如果用SVM,就涉及到映射到高维空间,这里用的是核函数,以及允许一些样本被分错,引入了松弛遍历。
另外映射到高维空间存在一个问题就是高维空间的计算复杂度很高,都是高维向量之间的乘积,如何解决这个问题,就要引入对偶问题,因为对偶问题显示跟新空间的维度没有关系,只跟样本数有关。
但由于利用核函数,就规避了在高维空间的向量计算问题,只在原向量空间维度进行向量计算即可,然后带入核函数。所以这里并没有讲对偶问题,如果对这部分感兴趣的话可以去看林轩田老师的课程,这部分也有详细的讲解
松弛变量和核函数的区别
个人感觉松弛变量和核函数都是为了解决线性不可分的问题,但两者还是存在很大的区别的
在原始的低维空间中,样本相当的不可分,无论怎么找分类平面,都会有大量的离群点,此时用核函数向高维空间映射,虽然结果有可能仍然是不可分的,但比原始空间里更接近线性可分的状态,此时再用松弛变量处理那些少数的顽固的离群点
核函数的比较
多项式核函数与线性函数的区别
多项式可以处理线性不可分的情况
但是三个参数的选择需要尝试
而且如果Q比较大的话,那么计算有点耗费资源
高斯核函数
无限多维转换,可以作出比较复杂的边界
参数少
可能会overfit
很常用,但由于转换到无限多维然后再分类,比较抽象,不好说是基于什么分类的
SVM实战
实质
算法的实质是求一系列的alpha,还有就是b,alpha就是前面提到的用拉格朗日乘子法消除约束条件前面的系数,一旦求出这些alpha值,就容易求得w权重向量以及分类超平面
首先同样是加载数据
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split(' ')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
然后是SVM的主体函数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
#创建一个alpha向量并将其初始化为0向量
alphas = mat(zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print "L==H"; continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print "eta>=0"; continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
#the update is in the oppostie direction
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
alphaPairsChanged += 1
print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
if (alphaPairsChanged == 0): iter += 1
else: iter = 0
print "iteration number: %d" % iter
return b,alphas
主体函数说明
参数说明
函数的输入为五个参数,其中C是惩罚因子,用于控制最大化间隔,toler是容错率
创建一个alpha向量并将其初始化为0向量
两层循环说明
主体是两层循环,外循环是设置最大迭代次数maxIter,如果迭代次数iter小于maxIter,就一直迭代
内循环是对数据集中的每个数据向量,进行遍历,总共m个数据样本,那么遍历m次
对于每一次循环如果这个数据向量可以被优化,随机选取另外一个数据向量,同时优化这两个向量,优化也就是修改这两个向量之前的alpha值,设置一个标志alphaPairsChanged用于记录是否有一个alpha被优化
SVM的目标函数如下,可见优化都是成对的优化

之所以要成对的优化,是因为约束条件的限制

如何优化
fxi计算得到预测的结果,本质上是计算wx+b的值,将预测的结果与真实值进行比较得到误差ei
如果误差很大,那么可以对该数据对应的alpha值进行优化,如何判断很大,实质上是看是否超过真实值的一个容忍范围
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0))
如果需要被优化,那么随机选取另外一个数据样本j以及对应的alpha值,与此前的alpha值组成alpha对
然后也计算数据样本j所预测的结果与真实值之间的偏差
然后计算alpha j的最优修正量eta
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
利用最优修正量对j进行修正
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
然后利用辅助函数将j缩短到L和H之间
alphas[j] = clipAlpha(alphas[j],H,L)
对i也进行修正
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
辅助函数
选择alpha的函数,随机从0到m中选取不等于i的alpha值
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
将alpha转换到L和H之间的函数
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj