HDU.P1100 Trees Made to Order 解题报告

http://www.cnblogs.com/keam37/p/3637717.html  keam所有 转载请注明出处

Problem Description

We can number binary trees using the following scheme:

我们用下面的规则来给一颗二叉树编号：
The empty tree is numbered 0.

空树编号为0。
The single-node tree is numbered 1.

只有一个节点的树编号为1。
All binary trees having m nodes have numbers less than all those having m+1 nodes.

所有m个节点的树的编号不会大于有m+1个节点的树的编号。
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either
Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.

任意一个编号为n，有m个节点，左右子树节点分别为L和R的二叉树。当一棵树的编号>n,不是该树的左子树的编号大于L，就是左子树编号相同，右子树编号大于R;
The first 10 binary trees and tree number 20 in this sequence are shown below:

前10颗二叉树和第20颗树如下所示:

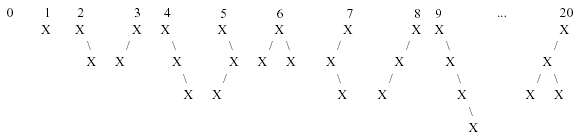
Your job for this problem is to output a binary tree when given its order number.

你的任务是依据给定编号,输出一颗树.

Input

Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)

Output

For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:
A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.

Sample Input

1

20

31117532 0

Sample Output

X

((X)X(X))X

(X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)

分析：

要打印这颗树，首先要确定树的节点数。

先用递推计算n个节点的树有多少颗，就能得到节点小于k的树一共有Sum[k]，这样对于输入的编号n

总的第n棵树,就是有k个节点的第（n-sum[k-1]）棵树.

再确定左右子树分别是总的第几棵树,再递归即可

参考代码

#include <iostream>
using namespace std;
//定义0个节点时有1种二叉树,用于递推
int radix[20] = {1};
int sRadix[20];
//递归求k个节点的第n颗树
int make (int n, int k)
{
            //只有一个节点时直接输出'X'
            if (k == 1) {
                    cout << 'X';
                    return 0;
            }
            //nL,nR代表左右子树的节点个数，sL，sR代表左右子树分别是当前节点数的第几颗树
            int nL = 0, sL = 0, nR = k - 1, sR = n;
            //如果sR>nR个节点最多二叉树的种数，左子树序号+1,p帮助累计左子树节点
            for (int p = 0; radix[nR] < sR; sL++) {
                    sR -= radix[nR];
                    if (p)  p--;
                    //如果p==0，左子树节点数+1，右节点数-1，更新p为nL个节点的左子树的种数-1
                    else {
                            nL++, nR--;
                            p = radix[nL] - 1;
                    }
            }
            //递归子树时为子树加上括号
            if (nL > 0) {
                    cout << '(';    make (sL - sRadix[nL - 1], nL);
                    cout << ')';
            }
            cout << 'X';
            if (nR > 0) {
                    cout << '(';    make (sR, nR);
                    cout << ')';
            }
            return 0;
}
int main()
{
            int n, k;
            //递推，求出radix[i]。代表i个节点的二叉树有几种
            for (int i = 1; i <= 18; i++) {
                    for (int j = 0; j <= (i - 1) / 2; j++)
                            radix[i] += radix[j] * radix[i - j - 1] * 2;
                    if (~ (i - 1) & 1) radix[i] -= radix[ (i - 1) / 2] * radix[ (i - 1) / 2];
                    //sRadix数组方便求出第N颗数有几个节点
                    sRadix[i] = sRadix[i - 1] + radix[i];
            }
            while (cin >> n && n) {
                    for (k = 1; sRadix[k] < n; k++);
                    make (n - sRadix[k - 1], k);
                    cout<<endl;
            }
            return 0;
}